Hostname: page-component-cb9f654ff-65tv2 Total loading time: 0 Render date: 2025-08-28T21:40:38.996Z Has data issue: false hasContentIssue false
  • English
  • Français

CONDITION (K) FOR BOOLEAN DYNAMICAL SYSTEMS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  27 May 2021

TOKE MEIER CARLSEN Open the ORCID record for TOKE MEIER CARLSEN [Opens in a new window]  and
EUN JI KANG Open the ORCID record for EUN JI KANG [Opens in a new window]
TOKE MEIER CARLSEN
Affiliation:
Department of Sciences and Technology, University of the Faroe Islands, Vestara Bryggja 15, FO-100 Tórshavn, Faroe Islands e-mail: toke.carlsen@gmail.com
EUN JI KANG*
Affiliation:
Research Institute of Mathematics, Seoul National University, Seoul 08826, Korea
*
e-mail: kkang33@snu.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize Condition (K) from directed graphs to Boolean dynamical systems and show that a locally finite Boolean dynamical system 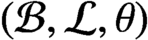$({{\mathcal {B}}},{{\mathcal {L}}},\theta )$ with countable 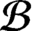${{\mathcal {B}}}$ and 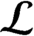${{\mathcal {L}}}$ satisfies Condition (K) if and only if every ideal of its $C^*$-algebra is gauge-invariant, if and only if its $C^*$-algebra has the (weak) ideal property, and if and only if its $C^*$-algebra has topological dimension zero. As a corollary we prove that if the $C^*$-algebra of a locally finite Boolean dynamical system with 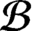${{\mathcal {B}}}$ and 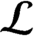${{\mathcal {L}}}$ countable either has real rank zero or is purely infinite, then 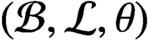$({{\mathcal {B}}}, {{\mathcal {L}}}, \theta )$ satisfies Condition (K). We also generalize the notion of maximal tails from directed graph to Boolean dynamical systems and use this to give a complete description of the primitive ideal space of the $C^*$-algebra of a locally finite Boolean dynamical system that satisfies Condition (K) and has countable 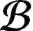${{\mathcal {B}}}$ and 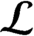${{\mathcal {L}}}$.

Keywords

C*-algebras of Boolean dynamical systemsCondition (K)gauge-invariant idealsgraph C*-algebrasideal propertymaximal tailprimitive ideal spacereal rank zerotopological dimension zeroultrafilter cycle

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 2 , April 2022 , pp. 145 - 169
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Aidan Sims

Research partially supported by NRF-2017R1D1A1B03030540.

References

Bates, T., Hong, J. H., Raeburn, I. and Szymański, W., ‘The ideal structure of the ${C}^{\ast }$ -algebras of infinite graphs’, Illinois J. Math. 46 (2002), 1159–1176.10.1215/ijm/1258138472CrossRefGoogle Scholar
Bates, T., Pask, D., Raeburn, I., and Szymański, W., ‘The ${C}^{\ast }$ -algebras of row-finite graphs’, New York J. Math. 6 (2000), 307–324.Google Scholar
Brown, L. G. and Pedersen, G. K., ‘ ${C}^{\ast }$ -algebras of real rank zero’, J. Funct. Anal. 99 (1991), 131–149.10.1016/0022-1236(91)90056-BCrossRefGoogle Scholar
Brown, L. G. and Pedersen, G. K., ‘Limits and ${C}^{\ast }$ -algebras of low rank or dimension’, J. Operator Theory 61(2) (2009), 318–417.Google Scholar
Carlsen, T. M. and Kang, E. J., ‘Gauge-invariant ideals of ${C}^{\ast }$ -algebras of Boolean dynamical systems’, J. Math. Anal. Appl. 488 (2020), 124037.10.1016/j.jmaa.2020.124037CrossRefGoogle Scholar
Carlsen, T. M. and Kang, E. J., ‘The ideal structure of ${C}^{\ast }$ -algebras of generalized Boolean dynamical systems’, in preparation.Google Scholar
Carlsen, T. M., Ortega, E. and Pardo, E., ‘ ${C}^{\ast }$ -algebras associated to Boolean dynamical systems’, J. Math. Anal. Appl. 450 (2017), 727–768.10.1016/j.jmaa.2017.01.038CrossRefGoogle Scholar
Carlsen, T. M. and Sims, A., ‘On Hong and Szymański’s description of the primitive-ideal space of a graph algebra’, in: Operator Algebras and Applications , Abel Symposia 12 (Springer, Cham, 2016), 109–126.10.1007/978-3-319-39286-8CrossRefGoogle Scholar
Connes, A., Noncommutative Geometry (Academic Press, San Diego, CA, 1994).Google Scholar
Dixmier, J., ${C}^{\ast }$ -Algebras, North-Holland Mathematical Library, 15 (North-Holland, Amsterdam, 1977).Google Scholar
Drinen, D. and Tomforde, M., ‘The ${C}^{\ast }$ -algebras of arbitrary graphs’, Rocky Mountain J. Math. 35 (2005), 105–135.10.1216/rmjm/1181069770CrossRefGoogle Scholar
Jeong, J. A., ‘Real rank of ${C}^{\ast }$ -algebras associated with graphs’, J. Aust. Math. Soc. 77 (2004), 141–147.10.1017/S1446788700010211CrossRefGoogle Scholar
Jeong, J. A., Kang, E. J. and Kim, S. H., ‘AF labeled graph ${C}^{\ast }$ -algebras’, J. Funct. Anal. 266 (2014), 2153–2173.10.1016/j.jfa.2013.10.001CrossRefGoogle Scholar
Jeong, J. A., Kang, E. J., Kim, S. H. and Park, G. H., ‘Finite simple labeled graph ${C}^{\ast }$ -algebras of Cantor minimal subshifts’, J. Math. Anal. Appl. 446 (2017), 395–410.10.1016/j.jmaa.2016.08.061CrossRefGoogle Scholar
Jeong, J. A., Kim, S. H. and Park, G. H., ‘The structure of gauge-invariant ideals of labeled graph ${C}^{\ast }$ -algebras’, J. Funct. Anal. 262 (2012), 1759–1780.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., ‘Non-simple purely finite ${C}^{\ast }$ -algebras’, Amer. J. Math. 122 (2000), 637–666.10.1353/ajm.2000.0021CrossRefGoogle Scholar
Kumjian, A., Pask, D. and Raeburn, I., ‘Cuntz–Krieger algebras of directed graphs’, Pacific J. Math. 184 (1998), 161–174.10.2140/pjm.1998.184.161CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids, and Cuntz–Krieger algebras’, J. Funct. Anal. 144 (1997), 505–541.CrossRefGoogle Scholar
Pasnicu, C. and Phillips, N. C., ‘Crossed products by spectrally free actions’, J. Funct. Anal. 269 (2015), 915–967.CrossRefGoogle Scholar
Pasnicu, C. and Phillips, N. C., ‘The weak ideal property and topological dimension zero’, Canad. J. Math. 69 (2017), 1385–1421.10.4153/CJM-2017-012-4CrossRefGoogle Scholar
Pasnicu, C. and Rørdam, M., ‘Purely infinite ${C}^{\ast }$ -algebras of real rank zero’, J. reine angew. Math. 613 (2007), 51–73.Google Scholar
Raeburn, I., Graph Algebras , CBMS Regional Conference Series in Mathematics, 103 (American Mathematical Society, Providence, RI, 2005).10.1090/cbms/103CrossRefGoogle Scholar
Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-Trace ${C}^{\ast }$ -Algebras, Surveys and Monographs, 60 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Webster, S., ‘The path space of a directed graph’, Proc. Amer. Math. Soc. 142 (2014), 213–225.10.1090/S0002-9939-2013-11755-7CrossRefGoogle Scholar