Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Serna, Juan D.
2015.
Partial Proof Without Words: Shaping Some Cases of the Erdős–Straus Conjecture.
The College Mathematics Journal,
Vol. 46,
Issue. 3,
p.
181.
Subburam, S.
and
Togbé, Alain
2016.
A note on the Erdős–Straus conjecture.
Periodica Mathematica Hungarica,
Vol. 72,
Issue. 1,
p.
43.
Elsholtz, Christian
2016.
EGYPTIAN FRACTIONS WITH ODD DENOMINATORS.
The Quarterly Journal of Mathematics,
Vol. 67,
Issue. 3,
p.
425.
Lapkova, Kostadinka
2016.
Explicit upper bound for an average number of divisors of quadratic polynomials.
Archiv der Mathematik,
Vol. 106,
Issue. 3,
p.
247.
Lapkova, Kostadinka
2017.
On the average number of divisors of reducible quadratic polynomials.
Journal of Number Theory,
Vol. 180,
Issue. ,
p.
710.
Lapkova, Kostadinka
2018.
Explicit upper bound for the average number of divisors of irreducible quadratic polynomials.
Monatshefte für Mathematik,
Vol. 186,
Issue. 4,
p.
663.
Bai, Tingting
2018.
On
1
w
+
1
x
+
1
y
+
1
z
=
1
2
$\frac{1}{w} + \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{1}{ 2} $
and some of its generalizations.
Journal of Inequalities and Applications,
Vol. 2018,
Issue. 1,
Garcia, Stephan Ramon
O’Neill, Christopher
and
Yih, Samuel
2019.
Factorization length distribution for affine semigroups I: Numerical semigroups with three generators.
European Journal of Combinatorics,
Vol. 78,
Issue. ,
p.
190.
Luca, Florian
and
Pappalardi, Francesco
2019.
On ternary Egyptian fractions with prime denominator.
Research in Number Theory,
Vol. 5,
Issue. 4,
Bright, Martin
and
Loughran, Daniel
2020.
Brauer–Manin obstruction for Erdős–Straus surfaces.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 4,
p.
746.
Elsholtz, Christian
and
Planitzer, Stefan
2020.
The number of solutions of the Erdős-Straus Equation and sums ofkunit fractions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 3,
p.
1401.
Ye, Dongxi
2020.
Revisiting the average number of divisors of a quadratic polynomial.
Monatshefte für Mathematik,
Vol. 192,
Issue. 2,
p.
465.
Luca, Florian
and
Pappalardi, Francesco
2021.
On the number of divisors of the least common multiples of shifted prime powers.
Functiones et Approximatio Commentarii Mathematici,
Vol. 64,
Issue. 2,
Gionfriddo, Mario
and
Guardo, Elena
2021.
A short proof of Erdös–Straus conjecture for everyn≡ 13 mod 24.
Journal of Interdisciplinary Mathematics,
Vol. 24,
Issue. 8,
p.
2307.
Elsholtz, Christian
and
Planitzer, Stefan
2021.
Sums of four and more unit fractions and approximate parametrizations.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 3,
p.
695.
Chiriac, Liubomir
2022.
The Average Number of Divisors in Certain Arithmetic Sequences.
Mathematica Pannonica,
Vol. 28_NS2,
Issue. 2,
p.
136.
Mond, Adva
and
Portier, Julien
2022.
Ternary Egyptian fractions with prime denominator.
Research in Number Theory,
Vol. 8,
Issue. 3,
 $n$, let
$n$, let 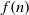 $f(n)$ denote the number of solutions to the Diophantine equation
$f(n)$ denote the number of solutions to the Diophantine equation 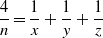 $$\begin{eqnarray*}\frac{4}{n} = \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\end{eqnarray*}$$
$$\begin{eqnarray*}\frac{4}{n} = \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\end{eqnarray*}$$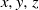 $x, y, z$ positive integers. The Erdős–Straus conjecture asserts that
$x, y, z$ positive integers. The Erdős–Straus conjecture asserts that 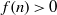 $f(n)\gt 0$ for every
$f(n)\gt 0$ for every 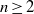 $n\geq 2$. In this paper we obtain a number of upper and lower bounds for
$n\geq 2$. In this paper we obtain a number of upper and lower bounds for 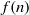 $f(n)$ or
$f(n)$ or 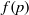 $f(p)$ for typical values of natural numbers
$f(p)$ for typical values of natural numbers  $n$ and primes
$n$ and primes 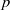 $p$. For instance, we establish that
$p$. For instance, we establish that 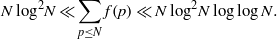 $$\begin{eqnarray*}N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\ll \displaystyle \sum _{p\leq N}f(p)\ll N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\log \log N.\end{eqnarray*}$$
$$\begin{eqnarray*}N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\ll \displaystyle \sum _{p\leq N}f(p)\ll N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\log \log N.\end{eqnarray*}$$
