Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stanton, R.G.
1997.
A retrospective look at the Erdős-DeBruijn theorem.
Journal of Statistical Planning and Inference,
Vol. 58,
Issue. 1,
p.
185.

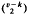 when
when 