No CrossRef data available.
Article contents
THE LATTICE OF VARIETIES OF STRICT LEFT RESTRICTION SEMIGROUPS
Published online by Cambridge University Press: 30 May 2018
Abstract
Left restriction semigroups are the unary semigroups that abstractly characterize semigroups of partial maps on a set, where the unary operation associates to a map the identity element on its domain. This paper is the sequel to two recent papers by the author, melding the results of the first, on membership in the variety 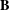 $\mathbf{B}$ of left restriction semigroups generated by Brandt semigroups and monoids, with the connection established in the second between subvarieties of the variety
$\mathbf{B}$ of left restriction semigroups generated by Brandt semigroups and monoids, with the connection established in the second between subvarieties of the variety 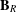 $\mathbf{B}_{R}$ of two-sided restriction semigroups similarly generated and varieties of categories, in the sense of Tilson. We show that the respective lattices
$\mathbf{B}_{R}$ of two-sided restriction semigroups similarly generated and varieties of categories, in the sense of Tilson. We show that the respective lattices 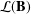 ${\mathcal{L}}(\mathbf{B})$ and
${\mathcal{L}}(\mathbf{B})$ and 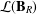 ${\mathcal{L}}(\mathbf{B}_{R})$ of subvarieties are almost isomorphic, in a very specific sense. With the exception of the members of the interval
${\mathcal{L}}(\mathbf{B}_{R})$ of subvarieties are almost isomorphic, in a very specific sense. With the exception of the members of the interval 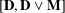 $[\mathbf{D},\mathbf{D}\vee \mathbf{M}]$, every subvariety of
$[\mathbf{D},\mathbf{D}\vee \mathbf{M}]$, every subvariety of 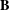 $\mathbf{B}$ is induced from a member of
$\mathbf{B}$ is induced from a member of 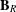 $\mathbf{B}_{R}$ and vice versa. Here
$\mathbf{B}_{R}$ and vice versa. Here 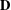 $\mathbf{D}$ is generated by the three-element left restriction semigroup
$\mathbf{D}$ is generated by the three-element left restriction semigroup 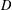 $D$ and
$D$ and 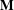 $\mathbf{M}$ is the variety of monoids. The analogues hold for pseudovarieties.
$\mathbf{M}$ is the variety of monoids. The analogues hold for pseudovarieties.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.

