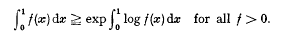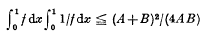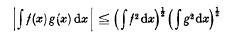Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mitrinović, Dragoslav S.
1970.
Analytic Inequalities.
p.
27.
Karlin, Samuel
and
Ziegler, Zvi
1976.
Some applications to inequalities of the method of generalized convexity.
Journal d'Analyse Mathématique,
Vol. 30,
Issue. 1,
p.
281.
Wang, Chung-Lie
1979.
On Development of Inverses of the Cauchy and Hölder Inequalities.
SIAM Review,
Vol. 21,
Issue. 4,
p.
550.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1993.
Classical and New Inequalities in Analysis.
p.
99.
Alpargu, Gülhan
and
Styan, George P. H.
2000.
Innovations in Multivariate Statistical Analysis.
Vol. 36,
Issue. ,
p.
1.
Yeh, Cheh-Chih
Hong, Huei-Lin
Li, Horng-Jaan
and
Yu, Shiueh-Ling
2006.
Some complements of Cauchy's inequality on time scales.
Journal of Inequalities and Applications,
Vol. 2006,
Issue. 1,
p.
97430.
Saxena, Ram K.
Daiya, Jitendra
and
Pogány, Tibor K.
2014.
Diaz-Metcalf and Pólya-Szegő type inequalities associated with Saigo fractional integral operator.
Tbilisi Mathematical Journal,
Vol. 7,
Issue. 2,
Milovanović, E.I.
and
Bekakos, M.P.
2017.
Sharp bounds for the general Randić index $R_-1$ of a graph.
Rocky Mountain Journal of Mathematics,
Vol. 47,
Issue. 1,
Zogić, E.
Borovičanin, B.
Milovanović, E.
and
Milovanović, I.
2018.
Randić degree-based energy of graphs.
Scientific Publications of the State University of Novi Pazar Series A: Applied Mathematics, Informatics and mechanics,
Vol. 10,
Issue. 2,
p.
99.
Milovanović, I.Ž.
Matejić, M.M.
and
Milovanović, E.I.
2018.
Upper bounds for arithmetic-geometric index of graphs.
Scientific Publications of the State University of Novi Pazar Series A: Applied Mathematics, Informatics and mechanics,
Vol. 10,
Issue. 1,
p.
49.
Matejić, M.M.
Milošević, P.D.
Milovanović, E.I.
and
Milovanović, I.Ž.
2019.
Remarks on general zeroth-order Randić and general sum-connectivity indices.
Scientific Publications of the State University of Novi Pazar Series A: Applied Mathematics, Informatics and mechanics,
Vol. 11,
Issue. 1,
p.
11.
Gutman, Ivan
MATEJIC, M.
MILOVANOVIC, E.
and
MILOVANOVIC, I.
2020.
Lower Bounds for Inverse Sum Indeg Index of Graphs.
Kragujevac Journal of Mathematics,
Vol. 44,
Issue. 4,
p.
551.
Hu, Xi-Mei
Tian, Jing-Feng
Chu, Yu-Ming
and
Lu, Yan-Xia
2020.
On Cauchy–Schwarz inequality for N-tuple diamond-alpha integral.
Journal of Inequalities and Applications,
Vol. 2020,
Issue. 1,
Atapour, Maryam
Jahanbani, Akbar
Khoeilar, Rana
and
Martinucci, Barbara
2021.
New Bounds for the Randić Index of Graphs.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.