Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rubinstein, Zalman
1986.
A variational method for the construction of convergent iterative sequences.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 41,
Issue. 1,
p.
51.

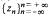 is established which has the properties
is established which has the properties 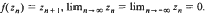 . The result certainly implies
. The result certainly implies 