Hostname: page-component-55f67697df-twqc4 Total loading time: 0 Render date: 2025-05-19T02:16:26.372Z Has data issue: false hasContentIssue false
  • English
  • Français

SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)

Part of: Miscellaneous topics in calculus of variations and optimal control General convexity Nonlinear operators and their properties

Published online by Cambridge University Press:  08 July 2014

JONATHAN M. BORWEIN  and
LIANGJIN YAO
JONATHAN M. BORWEIN
Affiliation:
CARMA, University of Newcastle, Newcastle, New South Wales 2308, Australia email jonathan.borwein@newcastle.edu.au
LIANGJIN YAO*
Affiliation:
CARMA, University of Newcastle, Newcastle, New South Wales 2308, Australia email liangjin.yao@newcastle.edu.au
*
✉liangjin.yao@newcastle.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The most important open problem in monotone operator theory concerns the maximal monotonicity of the sum of two maximally monotone operators provided that the classical Rockafellar’s constraint qualification holds. In this paper, we establish the maximal monotonicity of 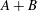$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A+B$ provided that 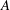$A$ and 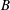$B$ are maximally monotone operators such that 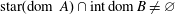${\rm star}({\rm dom}\ A)\cap {\rm int}\, {\rm dom}\, B\neq \varnothing $, and 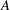$A$ is of type (FPV). We show that when also 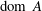${\rm dom}\ A$ is convex, the sum operator 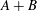$A+B$ is also of type (FPV). Our result generalizes and unifies several recent sum theorems.

Keywords

constraint qualificationconvex functionconvex setFitzpatrick functionlinear relationmaximally monotone operatormonotone operatoroperator of type (FPV)sum problem

MSC classification

Secondary: 47H05: Monotone operators and generalizations 49N15: Duality theory 52A41: Convex functions and convex programs 90C25: Convex programming
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 1 , August 2014 , pp. 1 - 26
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aragón Artacho, F. J., Borwein, J. M., Martín-Márquez, V. and Yao, L., ‘Applications of Convex Analysis within Mathematics’, Math. Program., to appear; doi:10.1007/s10107-013-0707-3.Google Scholar
Attouch, H. and Brezis, H., ‘Duality for the sum of convex functions in general Banach spaces’, in: Aspects of Mathematics and its Applications (ed. Barroso, J. A.) (Elsevier Science Publishers, Amsterdam, 1986), 125–133.Google Scholar
Attouch, H., Riahi, H. and Thera, M., ‘Somme ponctuelle d’operateurs maximaux monotones [Pointwise sum of maximal monotone operators] Well-posedness and stability of variational problems’, Serdica Math. J. 22 (1996), 165–190.Google Scholar
Bauschke, H. H. and Combettes, P. L., Convex Analysis and Monotone Operator Theory in Hilbert Spaces (Springer, Berlin, 2011).Google Scholar
Bauschke, H. H., Wang, X. and Yao, L., ‘An answer to S Simons’ question on the maximal monotonicity of the sum of a maximal monotone linear operator and a normal cone operator’, Set-Valued Var. Anal. 17 (2009), 195–201.CrossRefGoogle Scholar
Bauschke, H. H., Wang, X. and Yao, L., ‘On the maximal monotonicity of the sum of a maximal monotone linear relation and the subdifferential operator of a sublinear function’, in: Proceedings of the Haifa Workshop on Optimization Theory and Related Topics, Contemporary Mathematics, 568 (American Mathematical Society, Providence, RI, 2012), 19–26.Google Scholar
Borwein, J. M., ‘Maximal monotonicity via convex analysis’, J. Convex Anal. 13 (2006), 561–586.Google Scholar
Borwein, J. M., ‘Maximality of sums of two maximal monotone operators in general Banach space’, Proc. Amer. Math. Soc. 135 (2007), 3917–3924.Google Scholar
Borwein, J. M., ‘Fifty years of maximal monotonicity’, Optim. Lett. 4 (2010), 473–490.CrossRefGoogle Scholar
Borwein, J. M. and Lewis, A. S., Convex Analysis and Nonsmooth Optimization, Second expanded edition (Springer, New York, 2005).Google Scholar
Borwein, J. M. and Vanderwerff, J., Convex Functions: Constructions, Characterizations and Counterexamples, Encyclopedia of Mathematics and its Applications vol. 109 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Borwein, J. M. and Yao, L., ‘Structure theory for maximally monotone operators with points of continuity’, J. Optim. Theory Appl. 156 (2013), 1–24 (Invited paper).CrossRefGoogle Scholar
Borwein, J. M. and Yao, L., ‘Maximality of the sum of a maximally monotone linear relation and a maximally monotone operator’, Set-Valued Var. Anal. 21 (2013), 603–616.Google Scholar
Borwein, J. M. and Yao, L., ‘Some results on the convexity of the closure of the domain of a maximally monotone operator’, Optim. Lett. 8 (2014), 237–246.Google Scholar
Borwein, J. M. and Yao, L., ‘Recent progress on Monotone Operator Theory’ Infinite Products of Operators and Their Applications, Contemporary Mathematics, to appear;http://arxiv.org/abs/1210.3401v3.Google Scholar
Brøndsted, A. and Rockafellar, R. T., ‘On the subdifferentiability of convex functions’, Proc. Amer. Math. Soc. 16 (1995), 605–611.CrossRefGoogle Scholar
Burachik, R. S. and Iusem, A. N., Set-Valued Mappings and Enlargements of Monotone Operators (Springer, Berlin, 2008).Google Scholar
Butnariu, D. and Iusem, A. N., Totally Convex Functions for Fixed Points Computation and Infinite Dimensional Optimization (Kluwer Academic Publishers, Dordrecht, 2000).CrossRefGoogle Scholar
De Bernardi, C. and Veselý, L., ‘On support points and support functionals of convex sets’, Israel J. Math. 171 (2009), 15–27.Google Scholar
Fitzpatrick, S., ‘Representing monotone operators by convex functions’, in: Workshop/Miniconference on Functional Analysis and Optimization (Canberra 1988), Proceedings of the Centre for Mathematical Analysis vol. 20 (Australian National University, Canberra, Australia, 1988), 59–65.Google Scholar
Holmes, R. B., Geometric Functional Analysis and its Applications (Springer, New York, 1975).Google Scholar
Marques Alves, M. and Svaiter, B.F., ‘A new qualification condition for the maximality of the sum of maximal monotone operators in general Banach spaces’, J. Convex Anal. 19 (2012), 575–589.Google Scholar
Phelps, R. R., Convex Functions, Monotone Operators and Differentiability, 2nd edn (Springer, Berlin, 1993).Google Scholar
Phelps, R. R. and Simons, S., ‘Unbounded linear monotone operators on nonreflexive Banach spaces’, J. Nonlinear Convex Anal. 5 (1998), 303–328.Google Scholar
Rockafellar, R. T., ‘Local boundedness of nonlinear, monotone operators’, Michigan Math. J. 16 (1969), 397–407.Google Scholar
Rockafellar, R. T., Convex Analysis (Princeton University Press, Princeton, NJ, 1970).CrossRefGoogle Scholar
Rockafellar, R.T., ‘On the maximality of sums of nonlinear monotone operators’, Trans. Amer. Math. Soc. 149 (1970), 75–88.Google Scholar
Rockafellar, R. T. and Wets, R. J.-B., Variational Analysis, 3rd printing (Springer, Berlin, 2009).Google Scholar
Rudin, R., Functional Analysis, 2nd edn (McGraw-Hill, New York, 1991).Google Scholar
Simons, S., Minimax and Monotonicity (Springer, Berlin, 1998).Google Scholar
Simons, S., From Hahn-Banach to Monotonicity (Springer, Berlin, 2008).Google Scholar
Simons, S. and Zǎlinescu, C., ‘Fenchel duality, Fitzpatrick functions and maximal monotonicity’, J. Nonlinear Convex Anal. 6 (2005), 1–22.Google Scholar
Verona, A. and Verona, M.E., ‘Regular maximal monotone operators’, Set-Valued Anal. 6 (1998), 303–312.Google Scholar
Verona, A. and Verona, M.E., ‘Regular maximal monotone operators and the sum theorem’, J. Convex Anal. 7 (2000), 115–128.Google Scholar
Verona, A. and Verona, M.E., On the regularity of maximal monotone operators and related results, http://arxiv.org/abs/1212.1968v3 December 2012.Google Scholar
Veselý, L., ‘A parametric smooth variational principle and support properties of convex sets and functions’, J. Math. Anal. Appl. 350 (2009), 550–561.Google Scholar
Voisei, M. D., ‘The sum and chain rules for maximal monotone operators’, Set-Valued Var. Anal. 16 (2008), 461–476.Google Scholar
Voisei, M. D., ‘A Sum Theorem for (FPV) operators and normal cones’, J. Math. Anal. Appl. 371 (2010), 661–664.Google Scholar
Voisei, M. D. and Zălinescu, C., ‘Strongly-representable monotone operators’, J. Convex Anal. 16 (2009), 1011–1033.Google Scholar
Voisei, M. D. and Zălinescu, C., ‘Maximal monotonicity criteria for the composition and the sum under weak interiority conditions’, Math. Program. 123 (2010), 265–283.Google Scholar
Yao, L., ‘The sum of a maximal monotone operator of type (FPV) and a maximal monotone operator with full domain is maximally monotone’, Nonlinear Anal. 74 (2011), 6144–6152.CrossRefGoogle Scholar
Yao, L., On Monotone Linear Relations and the Sum Problem in Banach Spaces, PhD Thesis, University of British Columbia (Okanagan), 2011, http://hdl.handle.net/2429/39970.Google Scholar
Yao, L., ‘The sum of a maximally monotone linear relation and the subdifferential of a proper lower semicontinuous convex function is maximally monotone’, Set-Valued Var. Anal. 20 (2012), 155–167.Google Scholar
Zălinescu, C., Convex Analysis in General Vector Spaces (World Scientific Publishing, Singapore, 2002).Google Scholar
Zeidler, E., Nonlinear Functional Analysis and its Applications II/A: Linear Monotone Operators (Springer, Berlin, 1990).Google Scholar
Zeidler, E., Nonlinear Functional Analysis and its Applications II/B: Nonlinear Monotone Operators (Springer, Berlin, 1990).Google Scholar