Article contents
ALGEBRAIC FIBER SPACES AND CURVATURE OF HIGHER DIRECT IMAGES
Published online by Cambridge University Press: 03 September 2020
Abstract
Let 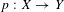 $p:X\rightarrow Y$ be an algebraic fiber space, and let
$p:X\rightarrow Y$ be an algebraic fiber space, and let  $L$ be a line bundle on
$L$ be a line bundle on 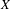 $X$. In this article, we obtain a curvature formula for the higher direct images of
$X$. In this article, we obtain a curvature formula for the higher direct images of 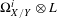 $\unicode[STIX]{x1D6FA}_{X/Y}^{i}\otimes L$ restricted to a suitable Zariski open subset of
$\unicode[STIX]{x1D6FA}_{X/Y}^{i}\otimes L$ restricted to a suitable Zariski open subset of 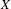 $X$. Our results are particularly meaningful if
$X$. Our results are particularly meaningful if  $L$ is semi-negatively curved on
$L$ is semi-negatively curved on 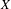 $X$ and strictly negative or trivial on smooth fibers of
$X$ and strictly negative or trivial on smooth fibers of 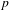 $p$. Several applications are obtained, including a new proof of a result by Viehweg–Zuo in the context of a canonically polarized family of maximal variation and its version for Calabi–Yau families. The main feature of our approach is that the general curvature formulas we obtain allow us to bypass the use of ramified covers – and the complications that are induced by them.
$p$. Several applications are obtained, including a new proof of a result by Viehweg–Zuo in the context of a canonically polarized family of maximal variation and its version for Calabi–Yau families. The main feature of our approach is that the general curvature formulas we obtain allow us to bypass the use of ramified covers – and the complications that are induced by them.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 973 - 1028
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
- 6
- Cited by


