Hostname: page-component-5db58dd55d-jnbmb Total loading time: 0 Render date: 2026-06-09T21:54:23.099Z Has data issue: false hasContentIssue false
  • English
  • Français

INVARIANT HYPERSURFACES

Part of: Differential and difference algebra Birational geometry

Published online by Cambridge University Press:  17 August 2020

Jason Bell ,
Rahim Moosa Open the ORCID record for Rahim Moosa [Opens in a new window]  and
Adam Topaz
Jason Bell
Affiliation:
University of Waterloo, Department of Pure Mathematics, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada (jpbell@uwaterloo.ca; rmoosa@uwaterloo.ca)
Rahim Moosa
Affiliation:
University of Waterloo, Department of Pure Mathematics, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada (jpbell@uwaterloo.ca; rmoosa@uwaterloo.ca)
Adam Topaz
Affiliation:
Mathematical and Statistical Sciences, University of Alberta, 632 Central Academic Building, Edmonton, Alberta T6G 2G1, Canada (topaz@ualberta.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

The following theorem, which includes as very special cases results of Jouanolou and Hrushovski on algebraic 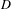$D$-varieties on the one hand, and of Cantat on rational dynamics on the other, is established: Working over a field of characteristic zero, suppose 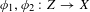$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}:Z\rightarrow X$ are dominant rational maps from an (possibly nonreduced) irreducible scheme 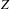$Z$ of finite type to an algebraic variety 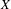$X$, with the property that there are infinitely many hypersurfaces on 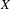$X$ whose scheme-theoretic inverse images under 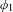$\unicode[STIX]{x1D719}_{1}$ and 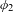$\unicode[STIX]{x1D719}_{2}$ agree. Then there is a nonconstant rational function $g$ on 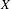$X$ such that 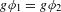$g\unicode[STIX]{x1D719}_{1}=g\unicode[STIX]{x1D719}_{2}$. In the case where 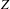$Z$ is also reduced, the scheme-theoretic inverse image can be replaced by the proper transform. A partial result is obtained in positive characteristic. Applications include an extension of the Jouanolou–Hrushovski theorem to generalised algebraic 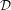${\mathcal{D}}$-varieties and of Cantat’s theorem to self-correspondences.

Keywords

D-varietydynamical systemfoliationgeneralised operatorhypersurfacerational mapself-correspondence

MSC classification

Primary: 14E99: None of the above, but in this section
Secondary: 12H05: Differential algebra 12H10: Difference algebra

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 713 - 739
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bell, J., Launois, S., Leon Sanchez, O. and Moosa, R., Poisson algebras via model theory and differential algebraic geometry, J. Eur. Math. Soc. 19(7) (2017), 2019–2049.CrossRefGoogle Scholar
Bell, J., Rogalski, D. and Sierra, S. J., The Dixmier–Moeglin equivalence for twisted homogeneous coordinate rings, Israel J. Math. 180 (2010), 461–507.CrossRefGoogle Scholar
Cantat, S., Invariant hypersurfaces in holomorphic dynamics, Math. Res. Lett. 17(5) (2010), 833–841.CrossRefGoogle Scholar
Freitag, J. and Moosa, R., Finiteness theorems on hypersurfaces in partial differential-algebraic geometry, Adv. Math. 314 (2017), 726–755.CrossRefGoogle Scholar
Hrushovski, E., Unpublished and untitled notes on ‘how to deduce the omega-categoricity of degree one strongly minimal sets in DCF from Jouanolou’s work’ dating from the mid-nineties.Google Scholar
Jouanolou, J. P., Hypersurfaces solutions d’une équation de Pfaff analytique, Math. Ann. 232(3) (1978), 239–245.10.1007/BF01351428CrossRefGoogle Scholar
Kolchin, E. R., Algebraic groups and algebraic dependence, Amer. J. Math. 90 (1968), 1151–1164.CrossRefGoogle Scholar
Krasnov, V. A., Compact complex manifolds without meromorphic functions, Mat. Zametki 17 (1975), 119–122.Google Scholar
Lang, S., Fundamentals of Diophantine Geometry (Springer, New York, 1983).CrossRefGoogle Scholar
Moosa, R. and Scanlon, T., Jet and prolongation spaces, J. Inst. Math. Jussieu 9(2) (2010), 391–430.CrossRefGoogle Scholar
Moosa, R. and Scanlon, T., Model theory of fields with free operators in characteristic zero, J. Math. Log. 14(2) (2014), 1450009, 43.Google Scholar