Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T06:49:08.879Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA

Part of: Algebraic geometry: Foundations Homotopy theory Categories with structure Homological algebra Applied homological algebra and category theory (Co)homology theory

Published online by Cambridge University Press:  25 May 2018

Dmitri Pavlov  and
Jakob Scholbach Open the ORCID record for Jakob Scholbach [Opens in a new window]
Dmitri Pavlov
Affiliation:
Faculty of Mathematics, University of Regensburg Department of Mathematics and Statistics, Texas Tech Universityhttps://dmitripavlov.org/
Jakob Scholbach
Affiliation:
Mathematical Institute, University of Münster, Germany https://wwwmath.uni-muenster.de/u/jakob.scholbach/
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper sets up the foundations for derived algebraic geometry, Goerss–Hopkins obstruction theory, and the construction of commutative ring spectra in the abstract setting of operadic algebras in symmetric spectra in an (essentially) arbitrary model category. We show that one can do derived algebraic geometry a la Toën–Vezzosi in an abstract category of spectra. We also answer in the affirmative a question of Goerss and Hopkins by showing that the obstruction theory for operadic algebras in spectra can be done in the generality of spectra in an (essentially) arbitrary model category. We construct strictly commutative simplicial ring spectra representing a given cohomology theory and illustrate this with a strictly commutative motivic ring spectrum representing higher order products on Deligne cohomology. These results are obtained by first establishing Smith’s stable positive model structure for abstract spectra and then showing that this category of spectra possesses excellent model-theoretic properties: we show that all colored symmetric operads in symmetric spectra valued in a symmetric monoidal model category are admissible, i.e., algebras over such operads carry a model structure. This generalizes the known model structures on commutative ring spectra and 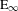$\text{E}_{\infty }$-ring spectra in simplicial sets or motivic spaces. We also show that any weak equivalence of operads in spectra gives rise to a Quillen equivalence of their categories of algebras. For example, this extends the familiar strictification of 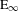$\text{E}_{\infty }$-rings to commutative rings in a broad class of spectra, including motivic spectra. We finally show that operadic algebras in Quillen equivalent categories of spectra are again Quillen equivalent. This paper is also available at arXiv:1410.5699v2.

Keywords

algebraic topologycategory theoryhomological algebrahomotopy theoryoperads

MSC classification

Primary: 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.) 55P48: Loop space machines, operads 18D50: Operads
Secondary: 55U40: Topological categories, foundations of homotopy theory 55P42: Stable homotopy theory, spectra 55U35: Abstract and axiomatic homotopy theory 18G55: Homotopical algebra 18D20: Enriched categories (over closed or monoidal categories) 14F42: Motivic cohomology; motivic homotopy theory 14F35: Homotopy theory; fundamental groups 14A20: Generalizations (algebraic spaces, stacks) 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 707 - 758
Creative Commons
This is a work of the U.S. Government and is not subject to copyright protection in the United States.
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The original version of this article was published with some references containing links to pirated websites. A notice detailing with this has been published and the error rectified in the online PDF and HTML copies.

References

Aguiar, M. and Mahajan, S., Monoidal Functors, Species and Hopf Algebras, CRM Monograph Series, Volume 29 (American Mathematical Society, Providence, RI, 2010), http://math.tamu.edu/∼maguiar/a.pdf.Google Scholar
Barwick, C., On left and right model categories and left and right Bousfield localizations, Homology Homotopy Appl. 12(2) (2010), 245–320, arXiv:0708.2067.Google Scholar
Batanin, M. and Berger, C., Homotopy theory for algebras over polynomial monads, Preprint, 2013, arXiv:1305.0086v6.Google Scholar
Behrend, K., Differential graded schemes I: perfect resolving algebras, Preprint, 2002, arXiv:math/0212225v1.Google Scholar
Beĭlinson, A. A., Higher Regulators and Values of L-Functions, Current Problems in Mathematics, Volume 24, pp. 181–238 (Itogi Nauki i Tekhniki, vol. 30, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform, Moscow, 1984), http://math.stanford.edu/∼conrad/BSDseminar/refs/BeilinsonConj.pdf.Google Scholar
Bayeh, M., Hess, K., Karpova, V., Kȩdziorek, M., Riehl, E. and Shipley, B., Left-induced model structures and diagram categories, in Women in Topology: Collaborations in Homotopy Theory, Contemporary Mathematics, Volume 641, pp. 49–81 (American Mathematical Society, Providence, RI, 2015), arXiv:1401.3651v2.Google Scholar
Berger, C. and Moerdijk, I., Axiomatic homotopy theory for operads, Comment. Math. Helv. 78(4) (2003), 805–831, arXiv:math/0206094.Google Scholar
Berger, C. and Moerdijk, I., On the derived category of an algebra over an operad, Georgian Math. J. 16(1) (2009), 13–28, arXiv:0801.2664v2.Google Scholar
Borceux, F., Handbook of Categorical Algebra. 1, Encyclopedia of Mathematics and its Applications, Volume 50 (Cambridge University Press, Cambridge, 1994).Google Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, Preprint, 2009, arXiv:0912.2110v3.Google Scholar
Deninger, C., Higher order operations in Deligne cohomology, Invent. Math. 120(2) (1995), 289–315. https://wwwmath.uni-muenster.de/u/weckerm/deninger/about/publikat/cd25.ps.Google Scholar
Elmendorf, A. D. and Mandell, M. A., Rings, modules, and algebras in infinite loop space theory, Adv. Math. 205(1) (2006), 163–228, arXiv:math/0403403.Google Scholar
Esnault, H. and Viehweg, E., Deligne–Beĭlinson Cohomology, Beĭlinson’s Conjectures on Special Values of L-Functions, Perspect. Math., Volume 4, pp. 43–91 (Academic Press, Boston, MA, 1988), http://mi.fu-berlin.de/users/esnault/preprints/ec/deligne_beilinson.pdf.Google Scholar
Fresse, B., Modules Over Operads and Functors, Lecture Notes in Mathematics, vol. 1967 (Springer, Berlin, 2009), arXiv:0704.3090v4.Google Scholar
Gorchinskiy, S. and Guletskii, V., Positive model structures for abstract symmetric spectra, Preprint, 2011. arXiv:1108.3509v3, http://dx.doi.org/10.1007/s10485-016-9480-9.Google Scholar
Gorchinskiy, S. and Guletskiĭ, V., Symmetric powers in abstract homotopy categories, Adv. Math. 292 (2016), 707–754, arXiv:0907.0730v4.Google Scholar
Goerss, P. G. and Hopkins, M. J., Moduli problems for structured ring spectra (June 8, 2005), http://math.northwestern.edu/∼pgoerss/spectra/obstruct.pdf.Google Scholar
Goerss, P. G. and Hopkins, M. J., Moduli Spaces of Commutative Ring Spectra, Structured Ring Spectra, London Mathematical Society Lecture Note Series, Volume 315, pp. 151–200 (Cambridge University Press, Cambridge, 2004), http://math.northwestern.edu/∼pgoerss/papers/sum.pdf.Google Scholar
Harper, J. E., Homotopy theory of modules over operads in symmetric spectra, Algebr. Geom. Topol. 9(3) (2009), 1637–1680, arXiv:0801.0193v3.Google Scholar
Harper, J. E., Homotopy theory of modules over operads and non-𝛴 operads in monoidal model categories, J. Pure Appl. Algebra 214(8) (2010), 1407–1434, arXiv:0801.0191.Google Scholar
Hinich, V., Homological algebra of homotopy algebras, Comm. Algebra 25(10) (1997), 3291–3323, arXiv:q-alg/9702015.Google Scholar
Hirschhorn, P. S., Model Categories and Their Localizations, Mathematical Surveys and Monographs, Volume 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Hornbostel, J., Preorientations of the derived motivic multiplicative group, Algebr. Geom. Topol. 13(5) (2013), 2667–2712, arXiv:1005.4546.Google Scholar
Hovey, M., Model Categories, Mathematical Surveys and Monographs, Volume 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M., Spectra and symmetric spectra in general model categories, J. Pure Appl. Algebra 165(1) (2001), 63–127, arXiv:math/0004051.Google Scholar
Hopkins, M. J. and Quick, G., Hodge filtered complex bordism, J. Topol. 8(1) (2015), 147–183, arXiv:1212.2173v3.Google Scholar
Hess, K. and Shipley, B., Waldhausen K-theory of spaces via comodules, Preprint, 2014. arXiv:1402.4719v2, http://dx.doi.org/10.1016/j.aim.2015.12.019.Google Scholar
Holmstrom, A. and Scholbach, J., Arakelov motivic cohomology I, J. Algebraic Geom. 24(4) (2015), 719–754, arXiv:1012.2523.Google Scholar
Hovey, M., Shipley, B. and Smith, J., Symmetric spectra, J. Amer. Math. Soc. 13(1) (2000), 149–208, arXiv:math/9801077.Google Scholar
Jardine, J. F., Motivic symmetric spectra, Doc. Math. 5 (2000), 445–553.Google Scholar
Lurie, J., Higher algebra (September 18, 2017), http://math.harvard.edu/∼lurie/papers/HA.pdf.Google Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, Volume 170 (Princeton University Press, Princeton, NJ, 2009), http://math.harvard.edu/∼lurie/papers/HTT.pdf.Google Scholar
Mandell, M. A., May, J. P., Schwede, S. and Shipley, B., Model categories of diagram spectra, Proc. Lond. Math. Soc. (3) 82(2) (2001), 441–512, http://www.math.uiuc.edu/K-theory/0320/.Google Scholar
Pereira, L. A., Cofibrancy of operadic constructions in positive symmetric spectra, Preprint, 2014, arXiv:1410.4816v2, http://dx.doi.org/10.4310/hha.2016.v18.n2.a7.Google Scholar
Pavlov, D. and Scholbach, J., Admissibility and rectification of colored symmetric operads, J. Topol. (to appear), Preprint, 2014, arXiv:1410.5675v3, https://doi.org/10.1112/topo.12008.Google Scholar
Pavlov, D. and Scholbach, J., Homotopy theory of symmetric powers, Homology, Homotopy Appl. 20(1) (2018), 359–397, arXiv:1510.04969v3, http://dx.doi.org/10.4310/HHA.2018.v20.n1.a20.Google Scholar
Richter, B., Symmetry properties of the Dold–Kan correspondence, Math. Proc. Cambridge Philos. Soc. 134(1) (2003), 95–102, http://www.math.uni-hamburg.de/home/richter/doldkan.pdf.Google Scholar
Saito, M., Mixed Hodge modules and applications, in Proceedings of the International Congress of Mathematicians, Volumes I, II (Kyoto 1990), pp. 725–734 (Mathematical Society, Japan, Tokyo, 1991), http://mathunion.org/ICM/ICM1990.1/Main/icm1990.1.0725.0734.ocr.pdf.Google Scholar
Scholbach, J., Special L-values of geometric motives, Asian Journal of Mathematics 21(2) (2017), 225–264, arXiv:1003.1215, http://dx.doi.org/10.4310/AJM.2017.v21.n2.a2.Google Scholar
Schwede, S., Spectra in model categories and applications to the algebraic cotangent complex, J. Pure Appl. Algebra 120(1) (1997), 77–104, http://people.math.uni-bonn.de/schwede/modelspec.pdf.Google Scholar
Schreiber, U., Differential cohomology in a cohesive infinity-topos, Preprint, 2013, arXiv:1310.7930v1.Google Scholar
Shipley, B., A convenient model category for commutative ring spectra, in Homotopy Theory: Relations With Algebraic Geometry, Group Cohomology, and Algebraic K-Theory, Contemporary Mathematics, Volume 346, pp. 473–483 (American Mathematical Society, Providence, RI, 2004), http://www.math.uic.edu/∼bshipley/com4.pdf.Google Scholar
Shipley, B., Hℤ-algebra spectra are differential graded algebras, Amer. J. Math. 129(2) (2007), 351–379, arXiv:math/0209215.Google Scholar
Spitzweck, M., Operads, algebras and modules in model categories and motives, Bonn: Univ. Bonn. Mathematisch-Naturwissenschaftliche Fakultät (Dissertation), 2001, http://d-nb.info/970107374/34.Google Scholar
Schwede, S. and Shipley, B. E., Algebras and modules in monoidal model categories, Proc. Lond. Math. Soc. (3) 80(2) (2000), 491–511, arXiv:math/9801082.Google Scholar
Schwede, S. and Shipley, B., Equivalences of monoidal model categories, Algebr. Geom. Topol. 3 (2003), 287–334, arXiv:math/0209342.Google Scholar
Schwede, S. and Shipley, B., Stable model categories are categories of modules, Topology 42(1) (2003), 103–153, arXiv:math/0108143.Google Scholar
Sagave, S. and Schlichtkrull, C., Diagram spaces and symmetric spectra, Adv. Math. 231(3–4) (2012), 2116–2193, arXiv:1103.2764.Google Scholar
Toën, B. and Vezzosi, G., Homotopical algebraic geometry. II. Geometric stacks and applications, Mem. Amer. Math. Soc. 193(902) (2008), x+224, arXiv:math/0404373.Google Scholar
White, D., Model structures on commutative monoids in general model categories, Preprint, 2014, arXiv:1403.6759v2, http://dx.doi.org/10.1016/j.jpaa.2017.03.001.Google Scholar
White, D., Monoidal Bousfield localizations and algebras over operads, Preprint, 2014, arXiv:1404.5197v1.Google Scholar