Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-28T04:14:51.768Z Has data issue: false hasContentIssue false
  • English
  • Français

BERRY–ESSEEN BOUND AND LOCAL LIMIT THEOREM FOR THE COEFFICIENTS OF PRODUCTS OF RANDOM MATRICES

Part of: Probability theory on algebraic and topological structures Limit theorems Ergodic theory

Published online by Cambridge University Press:  07 December 2022

Tien-Cuong Dinh ,
Lucas Kaufmann Open the ORCID record for Lucas Kaufmann [Opens in a new window]  and
Hao Wu
Tien-Cuong Dinh
Affiliation:
Department of Mathematics, National University of Singapore, 10, Lower Kent Ridge Road, Singapore 119076 (matdtc@nus.edu.sg)
Lucas Kaufmann*
Affiliation:
Center for Complex Geometry, Institute for Basic Science (IBS), 55 Expo-ro Yuseong-gu, Daejeon 34126 South Korea; Institut Denis Poisson, CNRS, Université d’Orléans, Rue de Chartres B.P. 6759, 45067 Orléans Cedex 2 France
Hao Wu
Affiliation:
Department of Mathematics, National University of Singapore, 10, Lower Kent Ridge Road, Singapore 119076 (matwu@nus.edu.sg)
*
lucas.kaufmann@univ-orleans.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 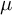$\mu $ be a probability measure on 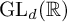$\mathrm {GL}_d(\mathbb {R})$, and denote by 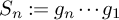$S_n:= g_n \cdots g_1$ the associated random matrix product, where 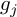$g_j$ are i.i.d. with law 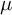$\mu $. Under the assumptions that 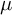$\mu $ has a finite exponential moment and generates a proximal and strongly irreducible semigroup, we prove a Berry–Esseen bound with the optimal rate 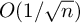$O(1/\sqrt n)$ for the coefficients of 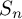$S_n$, settling a long-standing question considered since the fundamental work of Guivarc’h and Raugi. The local limit theorem for the coefficients is also obtained, complementing a recent partial result of Grama, Quint and Xiao.

MSC classification

Primary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization
Secondary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see ) 60F99: None of the above, but in this section 37A30: Ergodic theorems, spectral theory, Markov operators
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 2 , March 2024 , pp. 705 - 735
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, Y. and Quint, J.-F., ‘Central limit theorem for linear groups’, Ann. Probab. 44(2) (2016), 1308–1340.CrossRefGoogle Scholar
Benoist, Y. and Quint, J.-F., ‘Random Walks on Reductive Groups’, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 62 (Springer, Cham, 2016).Google Scholar
Bougerol, Philippe and Lacroix, Jean, ‘Products of Random Matrices with Applications to Schrödinger Operators’, Progress in Probability and Statistics, vol. 8 (Birkhäuser Boston, Inc., Boston, MA, 1985).CrossRefGoogle Scholar
Cuny, C., Dedecker, J. and Jan, C., ‘Limit theorems for the left random walk on ${\mathrm{GL}}_d\left(\mathbb{R}\right)$ ’, Ann. Inst. Henri Poincaré Probab. Stat., 53(4) (2017), 1839–1865.CrossRefGoogle Scholar
Cuny, C., Dedecker, J., Merlevède, F. and Peligrad, M., ‘Berry–Esseen type bounds for the left random walk on ${\mathrm{GL}}_d\left(\mathbb{R}\right)$ under polynomial moment conditions’, (2021), hal-03329189.Google Scholar
Cuny, C., Dedecker, J., Merlevède, F. and Peligrad, M.. ‘Berry–Esseen type bounds for the matrix coefficients and the spectral radius of the left random walk on $G{L}_d\left(\mathbb{R}\right)$ ’, C. R. Math. Acad. Sci. Paris 360 (2022), 475–482.CrossRefGoogle Scholar
Dinh, T.-C., Kaufmann, L. and Wu, H., ‘Products of random matrices: A dynamical point of view’, Pure Appl. Math. Q. 17(3) (2021), 933–969.CrossRefGoogle Scholar
Dinh, T.-C., Kaufmann, L. and Wu, H., ‘Random walks on ${\mathrm{SL}}_2\left(\mathbb{C}\right)$ : Spectral gap and limit theorems’, Preprint, 2021, arXiv:2106.04019.Google Scholar
Dinh, T.-C., Kaufmann, L. and Wu, H., ‘Berry–Esseen bounds with targets and local limit theorems for products of random matrices’, Preprint, 2022, arXiv:2111.14109. To appear in J. Geom. Anal..Google Scholar
Feller, W., ‘An Introduction to Probability Theory and Its Applications’, Vol. II, 2nd edn. (John Wiley & Sons, Inc., New York-London-Sydney, 1971).Google Scholar
Fernando, K. and Pène, F., ‘Expansions in the local and the central limit theorems for dynamical systems’, Preprint, 2020, arXiv:2008.08726.Google Scholar
Furstenberg, H., ‘Noncommuting random products’, Trans. Amer. Math. Soc. 108 (1963), 377–428.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H., ‘Products of random matrices’, Ann. Math. Statist. 31 (1960), 457–469.CrossRefGoogle Scholar
Grama, I., Quint, J.-F. and Xiao, H., ‘A zero-one law for invariant measures and a local limit theorem for coefficients of random walks on the general linear group’, Preprint, 2020, arXiv:2009.11593.Google Scholar
Guivarc’h., Y. ‘Produits de matrices aléatoires et applications aux propriétés géométriques des sous-groupes du groupe linéaire’, Ergodic Theory Dynam. Systems 10(3) (1990), 483–512.CrossRefGoogle Scholar
Guivarc’h., Y. and Raugi., A., ‘Frontière de Furstenberg, propriétés de contraction et théorèmes de convergence’, Z. Wahrsch. Verw. Gebiete 69(2) (1985), 187–242.CrossRefGoogle Scholar
Jirak, M., ‘Berry–Esseen theorems under weak dependence’, Ann. Probab. 44(3) (2016), 2024–2063.CrossRefGoogle Scholar
Le Page, É., ‘Théorèmes limites pour les produits de matrices aléatoires’, in Probability Measures on Groups (Oberwolfach, 1981), Lecture Notes in Math., vol. 928 (Springer, Berlin-New York, 1982), 258–303.CrossRefGoogle Scholar
Triebel, H., ‘Interpolation Theory, Function Spaces, Differential Operators’, North-Holland Mathematical Library, vol. 18 (North-Holland Publishing Co., Amsterdam-New York, 1978).Google Scholar
Xiao, H., Grama, I. and Liu, Q., ‘Berry–Esseen bounds and moderate deviations for the random walks on ${\mathrm{GL}}_d\left(\mathbb{R}\right)$ ’, Stochastic Process. Appl. 142 (2021), 293–318.CrossRefGoogle Scholar
Xiao, H., Grama, I. and Liu, Q., ‘Berry–Esseen bounds and moderate deviations for the norm, entries and spectral radius of products of positive random matrices’, Preprint, 2020, arXiv:2010.00557.Google Scholar
Xiao, H., Grama, I. and Liu, Q., ‘Large deviation expansions for the coefficients of random walks on the general linear group’, Preprint, 2020, arXiv:2010.00553.Google Scholar