Article contents
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES
Published online by Cambridge University Press: 02 August 2017
Abstract
Let 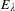 $E_{\unicode[STIX]{x1D706}}$ be the Legendre family of elliptic curves. Given
$E_{\unicode[STIX]{x1D706}}$ be the Legendre family of elliptic curves. Given  $n$ points
$n$ points 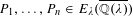 $P_{1},\ldots ,P_{n}\in E_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}(\unicode[STIX]{x1D706})})$, linearly independent over
$P_{1},\ldots ,P_{n}\in E_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}(\unicode[STIX]{x1D706})})$, linearly independent over  $\mathbb{Z}$, we prove that there are at most finitely many complex numbers
$\mathbb{Z}$, we prove that there are at most finitely many complex numbers 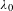 $\unicode[STIX]{x1D706}_{0}$ such that
$\unicode[STIX]{x1D706}_{0}$ such that 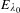 $E_{\unicode[STIX]{x1D706}_{0}}$ has complex multiplication and
$E_{\unicode[STIX]{x1D706}_{0}}$ has complex multiplication and 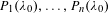 $P_{1}(\unicode[STIX]{x1D706}_{0}),\ldots ,P_{n}(\unicode[STIX]{x1D706}_{0})$ are linearly dependent over End
$P_{1}(\unicode[STIX]{x1D706}_{0}),\ldots ,P_{n}(\unicode[STIX]{x1D706}_{0})$ are linearly dependent over End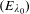 $(E_{\unicode[STIX]{x1D706}_{0}})$. This implies a positive answer to a question of Bertrand and, combined with a previous work in collaboration with Capuano, proves the Zilber–Pink conjecture for a curve in a fibered power of an elliptic scheme when everything is defined over
$(E_{\unicode[STIX]{x1D706}_{0}})$. This implies a positive answer to a question of Bertrand and, combined with a previous work in collaboration with Capuano, proves the Zilber–Pink conjecture for a curve in a fibered power of an elliptic scheme when everything is defined over  $\overline{\mathbb{Q}}$.
$\overline{\mathbb{Q}}$.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 5 , September 2019 , pp. 941 - 956
- Copyright
- © Cambridge University Press 2017
Footnotes
F. B. was supported by the EPSRC grant EP/N007956/1’ and the SNF grant 165525.
References
A correction has been issued for this article:
- 4
- Cited by
Linked content
Please note a has been issued for this article.

