Article contents
THE CRAMÉR–WOLD THEOREM ON QUADRATIC SURFACES AND HEISENBERG UNIQUENESS PAIRS
Published online by Cambridge University Press: 07 November 2017
Abstract
Two measurable sets 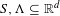 $S,\unicode[STIX]{x1D6EC}\subseteq \mathbb{R}^{d}$ form a Heisenberg uniqueness pair, if every bounded measure
$S,\unicode[STIX]{x1D6EC}\subseteq \mathbb{R}^{d}$ form a Heisenberg uniqueness pair, if every bounded measure  $\unicode[STIX]{x1D707}$ with support in
$\unicode[STIX]{x1D707}$ with support in  $S$ whose Fourier transform vanishes on
$S$ whose Fourier transform vanishes on 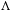 $\unicode[STIX]{x1D6EC}$ must be zero. We show that a quadratic hypersurface and the union of two hyperplanes in general position form a Heisenberg uniqueness pair in
$\unicode[STIX]{x1D6EC}$ must be zero. We show that a quadratic hypersurface and the union of two hyperplanes in general position form a Heisenberg uniqueness pair in 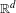 $\mathbb{R}^{d}$. As a corollary we obtain a new, surprising version of the classical Cramér–Wold theorem: a bounded measure supported on a quadratic hypersurface is uniquely determined by its projections onto two generic hyperplanes (whereas an arbitrary measure requires the knowledge of a dense set of projections). We also give an application to the unique continuation of eigenfunctions of second-order PDEs with constant coefficients.
$\mathbb{R}^{d}$. As a corollary we obtain a new, surprising version of the classical Cramér–Wold theorem: a bounded measure supported on a quadratic hypersurface is uniquely determined by its projections onto two generic hyperplanes (whereas an arbitrary measure requires the knowledge of a dense set of projections). We also give an application to the unique continuation of eigenfunctions of second-order PDEs with constant coefficients.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 117 - 135
- Copyright
- © Cambridge University Press 2017
References
- 13
- Cited by

