No CrossRef data available.
Article contents
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
Published online by Cambridge University Press: 15 December 2014
Abstract
We consider the distribution of 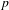 $p$ -power group schemes among the torsion of abelian varieties over finite fields of characteristic
$p$ -power group schemes among the torsion of abelian varieties over finite fields of characteristic 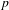 $p$ , as follows. Fix natural numbers
$p$ , as follows. Fix natural numbers  $g$ and
$g$ and  $n$ , and let
$n$ , and let  ${\it\xi}$ be a non-supersingular principally quasipolarized Barsotti–Tate group of level
${\it\xi}$ be a non-supersingular principally quasipolarized Barsotti–Tate group of level  $n$ . We classify the
$n$ . We classify the 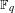 $\mathbb{F}_{q}$ -rational forms
$\mathbb{F}_{q}$ -rational forms 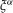 ${\it\xi}^{{\it\alpha}}$ of
${\it\xi}^{{\it\alpha}}$ of  ${\it\xi}$ . Among all principally polarized abelian varieties
${\it\xi}$ . Among all principally polarized abelian varieties 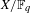 $X/\mathbb{F}_{q}$ of dimension
$X/\mathbb{F}_{q}$ of dimension  $g$ with
$g$ with 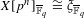 $X[p^{n}]_{\bar{\mathbb{F}}_{q}}\cong {\it\xi}_{\bar{\mathbb{F}}_{q}}$ , we compute the frequency with which
$X[p^{n}]_{\bar{\mathbb{F}}_{q}}\cong {\it\xi}_{\bar{\mathbb{F}}_{q}}$ , we compute the frequency with which 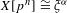 $X[p^{n}]\cong {\it\xi}^{{\it\alpha}}$ . The error in our estimate is bounded by
$X[p^{n}]\cong {\it\xi}^{{\it\alpha}}$ . The error in our estimate is bounded by 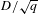 $D/\sqrt{q}$ , where
$D/\sqrt{q}$ , where 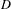 $D$ depends on
$D$ depends on  $g$ ,
$g$ ,  $n$ , and
$n$ , and 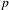 $p$ , but not on
$p$ , but not on  ${\it\xi}$ .
${\it\xi}$ .
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 693 - 710
- Copyright
- © Cambridge University Press 2014

