No CrossRef data available.
Article contents
THE EISENSTEIN IDEAL OF WEIGHT k AND RANKS OF HECKE ALGEBRAS
Published online by Cambridge University Press: 31 March 2023
Abstract
Let p and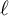 
$\ell $ be primes such that 
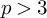$p> 3$ and 
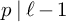$p \mid \ell -1$ and k be an even integer. We use deformation theory of pseudo-representations to study the completion of the Hecke algebra acting on the space of cuspidal modular forms of weight k and level 
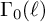$\Gamma _0(\ell )$ at the maximal Eisenstein ideal containing p. We give a necessary and sufficient condition for the 
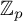$\mathbb {Z}_p$-rank of this Hecke algebra to be greater than 
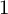$1$ in terms of vanishing of the cup products of certain global Galois cohomology classes. We also recover some of the results proven by Wake and Wang-Erickson for 
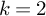$k=2$ using our methods. In addition, we prove some 
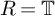$R=\mathbb {T}$ theorems under certain hypotheses.
MSC classification
Primary:
11F80: Galois representations
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 2 , March 2024 , pp. 983 - 1017
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
Dedicated to the memory of my father Vilas G. Deo.
References
Bellaïche, J., ‘Image of pseudo-representations and coefficients of modular forms modulo
$p$
’, Adv. Math. 353 (2019), 647–721.CrossRefGoogle Scholar
$p$
’, Adv. Math. 353 (2019), 647–721.CrossRefGoogle ScholarBellaïche, J. and Chenevier, G., ‘Lissite de la courbe de Hecke de
$\mathrm{GL}(2)$
aux points Eisenstein critiques’, J. Inst. Math. Jussieu 5(2) (2006), 333–349.CrossRefGoogle Scholar
$\mathrm{GL}(2)$
aux points Eisenstein critiques’, J. Inst. Math. Jussieu 5(2) (2006), 333–349.CrossRefGoogle ScholarBellaïche, J. and Chenevier, G., ‘Families of Galois representations and Selmer groups’, Astérisque 324 (2009), pp. xii+314.Google Scholar
Bellaïche, J. and Khare, C., ‘Level
$1$
Hecke algebras of modular forms modulo
$p$
,’ Compos. Math. 151(3) (2015), 397–415.CrossRefGoogle Scholar
$1$
Hecke algebras of modular forms modulo
$p$
,’ Compos. Math. 151(3) (2015), 397–415.CrossRefGoogle ScholarCalegari, F. and Emerton, M., ‘On the ramification of Hecke algebras at Eisenstein primes’, Invent. Math. 160(1) (2005), 97—144.CrossRefGoogle Scholar
Calegari, F. and Specter, J., ‘Pseudorepresentations of weight one are unramified’, Algebra Number Theory 13(7) (2019), 1583–1596.CrossRefGoogle Scholar
Chenevier, G., The
$p$
-adic analytic space of pseudocharacters of a profinite group and pseudorepresentations over arbitrary rings, in Automorphic Forms and Galois Representations. vol. 1, London Math. Soc. Lecture Note Ser. 414, (Cambridge Univ. Press, Cambridge, 2014), 221–285.CrossRefGoogle Scholar
$p$
-adic analytic space of pseudocharacters of a profinite group and pseudorepresentations over arbitrary rings, in Automorphic Forms and Galois Representations. vol. 1, London Math. Soc. Lecture Note Ser. 414, (Cambridge Univ. Press, Cambridge, 2014), 221–285.CrossRefGoogle ScholarDeo, S. V., ‘Effect of increasing the ramification on pseudo-deformation rings’, J. Théor. Nombres Bordeaux 34(1) (2022), 189–236.CrossRefGoogle Scholar
Deo, S. V., ‘On density of modular points in pseudo-deformation rings’, To appear in Int. Math. Res. Not. IMRN.
Google Scholar
de Smit, B., Rubin, K. and Schoof, R., Criteria for complete intersections, in Modular Forms and Fermat’s Last Theorem (Springer, New York, 1997), 343–356.CrossRefGoogle Scholar
Sikirić, M. Dutour, Elbaz-Vincent, P., Kupers, A. and Martinet, J., Voronoi complexes in higher dimensions, cohomology of
${\mathrm{GL}}_N(\mathbb{Z})$
for
$N\ge 8$
and the triviality of
${K}_8(\mathbb{Z})$
, Preprint, https://arxiv.org/pdf/1910.11598.pdf.Google Scholar
${\mathrm{GL}}_N(\mathbb{Z})$
for
$N\ge 8$
and the triviality of
${K}_8(\mathbb{Z})$
, Preprint, https://arxiv.org/pdf/1910.11598.pdf.Google ScholarEisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, Grad. Texts in Math. 150 (Springer-Verlag, New York, 1995).Google Scholar
Gross, B., ‘A tameness criterion for Galois representations associated to modular forms
$(mod\ p)$
’, Duke Math. J. 61(2) (1990), 445–517.CrossRefGoogle Scholar
$(mod\ p)$
’, Duke Math. J. 61(2) (1990), 445–517.CrossRefGoogle ScholarJochnowitz, N., ‘Congruences between systems of eigenvalues of modular forms’, Trans. Amer. Math. Soc. 270(1) (1982), 269–285.CrossRefGoogle Scholar
Kurihara, M., Some remarks on conjectures about cyclotomic fields and
$K$
-groups of
$\mathbb{Z}$
, Compos. Math. 81 (1992), 223–236.Google Scholar
$K$
-groups of
$\mathbb{Z}$
, Compos. Math. 81 (1992), 223–236.Google ScholarLecouturier, E., ‘On the Galois structure of the class group of certain Kummer extensions’, J. Lond. Math. Soc. 98(1) (2018), 35–58.CrossRefGoogle Scholar
Lecouturier, E., ‘Higher Eisenstein elements, higher Eichler formulas and rank of Hecke algebras’, Invent. Math. 223(2) (2021), 485–595.CrossRefGoogle Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Publ. Math. Inst. Hautes Études Sci. 47 (1977), 33–186.CrossRefGoogle Scholar
Mazur, B., Deforming Galois representations, in Galois Groups Over
$\mathbb{Q}$
, Math. Sci. Res. Inst. Publ. 16 (Springer, New York, 1989), 385–437.Google Scholar
$\mathbb{Q}$
, Math. Sci. Res. Inst. Publ. 16 (Springer, New York, 1989), 385–437.Google ScholarMerel, L., L’accouplement de Weil entre le sous-groupe de Shimura et le sous-groupe cuspidal de
${J}_0(p)$
, J. Reine Angew. Math. 477 (1996), 71–115.Google Scholar
${J}_0(p)$
, J. Reine Angew. Math. 477 (1996), 71–115.Google ScholarOhta, M., ‘Eisenstein ideals and the rational torsion subgroups of modular Jacobian varieties II’, Tokyo J. Math. 37 (2014), 273–318.CrossRefGoogle Scholar
Osburn, R., ‘Vanishing of eigenspaces and cyclotomic fields’, Int. Math. Res. Not. IMRN 20 (2005), 1195–1202.CrossRefGoogle Scholar
Ramakrishna, R., ‘On a variation of Mazur’s deformation functor’, Compos. Math. 87 (1993), 269–286.Google Scholar
Schaefer, K. and Stubley, E., ‘Class groups of Kummer extensions via cup product in Galois cohomology’, Trans. Amer. Math. Soc. 372(10) (2019), 6927–6980.CrossRefGoogle Scholar
Wake, P., The Eisenstein ideal for weight
$k$
and a Bloch-Kato conjecture for tame families, To appear in J. Eur. Math. Soc. (JEMS).Google Scholar
$k$
and a Bloch-Kato conjecture for tame families, To appear in J. Eur. Math. Soc. (JEMS).Google ScholarWake, P. and Wang-Erickson, C., Deformation conditions for pseudorepresentations, Forum Math. Sigma 7 (2019), Paper No. e20, 44 pp.CrossRefGoogle Scholar
Wake, P. and Wang-Erickson, C., ‘The rank of Mazur’s Eisenstein ideal’, Duke Math. J. 169(1) (2020), 31–115.CrossRefGoogle Scholar
Wake, P. and Wang-Erickson, C., ‘The Eisenstein ideal with squarefree level’, Adv. Math. 380 (2021), Paper No. 107543, 62 pp.CrossRefGoogle Scholar
Washington, L., Introduction to Cyclotomic Fields, Grad. Texts in Math. 83 (Springer-Verlag, New York, 1982).CrossRefGoogle Scholar
Washington, L., Galois cohomology, in Modular Forms and Fermat’s Last Theorem (Springer, New York, 1997), 101–120.CrossRefGoogle Scholar