Hostname: page-component-7f64f4797f-d7bbv Total loading time: 0 Render date: 2025-11-03T10:18:20.415Z Has data issue: false hasContentIssue false
  • English
  • Français

FRAMED CORRESPONDENCES AND THE MILNOR–WITT 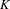$K$-THEORY

Part of: (Co)homology theory

Published online by Cambridge University Press:  30 June 2016

Alexander Neshitov
Alexander Neshitov*
Affiliation:
Alexander Neshitov, Steklov Mathematical Institute, St. Petersburg, Russia (alexander.neshitov@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a field 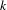$k$ of characteristic zero and 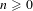$n\geqslant 0$, we prove that 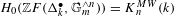$H_{0}(\mathbb{Z}F(\unicode[STIX]{x1D6E5}_{k}^{\bullet },\mathbb{G}_{m}^{\wedge n}))=K_{n}^{MW}(k)$, where 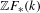$\mathbb{Z}F_{\ast }(k)$ is the category of linear framed correspondences of algebraic 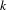$k$-varieties, introduced by Garkusha and Panin [The triangulated category of linear framed motives 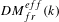$DM_{fr}^{eff}(k)$, in preparation] (see [Garkusha and Panin, Framed motives of algebraic varieties (after V. Voevodsky), Preprint, 2014, arXiv:1409.4372], § 7 as well), and 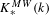$K_{\ast }^{MW}(k)$ is the Milnor–Witt 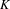$K$-theory of the base field 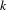$k$.

Keywords

framed correspondencesMilnor–Witt K-theory

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 14F99: None of the above, but in this section

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 4 , September 2018 , pp. 823 - 852
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The work was supported by the Russian Science Foundation grant 14-11-00456.

References

Balmer, P. and Walter, C., A Gersten–Witt spectral sequence for regular schemes, Ann. Sci. Éc. Norm. Supér. (4) 35(1) (2002), 127–152.Google Scholar
Fasel, J., The Chow–Witt ring, Doc. Math. 12 (2007), 275–312.Google Scholar
Fasel, J., Groupes de Chow–Witt, Mém. Soc. Math. Fr. (N.S.) 113 (2008), viii+197 pp.Google Scholar
Fasel, J., A degree map on unimodular rows, J. Ramanujan Math. Soc. 27(1) (2012), 23–42.Google Scholar
Garkusha, G. and Panin, I., Framed Motives of algebraic varieties (after V. Voevodsky), Preprint, 2014, arXiv:1409.4372.Google Scholar
Garkusha, G. and Panin, I., The triangulated category of linear framed motives $DM_{fr}^{eff}(k)$ , in preparation.Google Scholar
Gille, S., A transfer morphism for Witt groups, J. Reine Angew. Math. 564 (2003), 215–233.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Volume 52 (Springer-Verlag, New York–Heidelberg, 1977).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture Notes on Motivic Cohomology, Clay Mathematics Monographs, Volume 2 (American Mathematical Society, Providence, RI, 2006). Clay Mathematics Institute, Cambridge, MA.Google Scholar
Morel, F., A1 -Algebraic Topology Over a Field, Lecture Notes in Mathematics, Volume 2052 (Springer, Heidelberg, 2012).Google Scholar
Scharlau, W., Quadratic and Hermitian Forms, Grundlehren der Mathematischen Wissenschaften, Volume 270 (Springer, Berlin, Heidelberg, 1985).Google Scholar
Voevodsky, V., Notes on framed correspondences, unpublished (2001–2003).Google Scholar