Article contents
FROM THE FUNCTION-SHEAF DICTIONARY TO QUASICHARACTERS OF 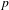 $p$ -ADIC TORI
$p$ -ADIC TORI
Published online by Cambridge University Press: 13 October 2015
Abstract
We consider the rigid monoidal category of character sheaves on a smooth commutative group scheme 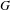 $G$ over a finite field
$G$ over a finite field 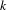 $k$ , and expand the scope of the function-sheaf dictionary from connected commutative algebraic groups to this setting. We find the group of isomorphism classes of character sheaves on
$k$ , and expand the scope of the function-sheaf dictionary from connected commutative algebraic groups to this setting. We find the group of isomorphism classes of character sheaves on 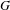 $G$ , and show that it is an extension of the group of characters of
$G$ , and show that it is an extension of the group of characters of 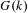 $G(k)$ by a cohomology group determined by the component group scheme of
$G(k)$ by a cohomology group determined by the component group scheme of 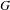 $G$ . We also classify all morphisms in the category character sheaves on
$G$ . We also classify all morphisms in the category character sheaves on 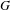 $G$ . As an application, we study character sheaves on Greenberg transforms of locally finite type Néron models of algebraic tori over local fields. This provides a geometrization of quasicharacters of
$G$ . As an application, we study character sheaves on Greenberg transforms of locally finite type Néron models of algebraic tori over local fields. This provides a geometrization of quasicharacters of 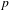 $p$ -adic tori.
$p$ -adic tori.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 1 , February 2018 , pp. 1 - 37
- Copyright
- © Cambridge University Press 2015
References
- 2
- Cited by

