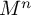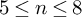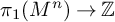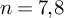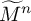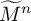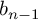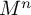Introduction
We prove here the following theorem. Every hyperbolic manifold in this paper is tacitly assumed to be connected, complete and orientable.
Theorem 1. In every dimension
![]() $5 \leq n \leq 8$
, there are a finite volume hyperbolic n-manifold
$5 \leq n \leq 8$
, there are a finite volume hyperbolic n-manifold
![]() $M^n$
and a map
$M^n$
and a map
![]() $f \colon M^n \to S^1$
, such that
$f \colon M^n \to S^1$
, such that
![]() $f_* \colon \pi _1(M^n) \to {\mathbb {Z}}$
is surjective with finitely generated kernel. The cover
$f_* \colon \pi _1(M^n) \to {\mathbb {Z}}$
is surjective with finitely generated kernel. The cover
![]() $\widetilde M^n = {\mathbb {H}}^n/{\ker f_*}$
has infinitely many cusps of maximal rank. When
$\widetilde M^n = {\mathbb {H}}^n/{\ker f_*}$
has infinitely many cusps of maximal rank. When
![]() $n=7,8$
, the kernel is also finitely presented.
$n=7,8$
, the kernel is also finitely presented.
We deduce, in particular, the following.
Corollary 2. In dimension
![]() $n=7,8$
, there is a hyperbolic n-manifold with finitely presented fundamental group and infinitely many cusps of maximal rank. The manifold covers a finite-volume hyperbolic manifold.
$n=7,8$
, there is a hyperbolic n-manifold with finitely presented fundamental group and infinitely many cusps of maximal rank. The manifold covers a finite-volume hyperbolic manifold.
The same assertion holds in the dimensions
![]() $n=5,6$
, with ‘finitely generated’ replacing ‘finitely presented’.
$n=5,6$
, with ‘finitely generated’ replacing ‘finitely presented’.
For every
![]() $5\leq n \leq 8$
, the group
$5\leq n \leq 8$
, the group
![]() $\pi _1(M^n)$
is a finite-index subgroup of the arithmetic lattice
$\pi _1(M^n)$
is a finite-index subgroup of the arithmetic lattice
![]() $\mathrm {O}(n,1, {\mathbb {Z}})$
. Recall that a group
$\mathrm {O}(n,1, {\mathbb {Z}})$
. Recall that a group
![]() $\Gamma $
is of finite type, denoted
$\Gamma $
is of finite type, denoted
![]() $\mathrm {F}$
, if it has a finite classifying space, and of type
$\mathrm {F}$
, if it has a finite classifying space, and of type
![]() $\mathrm {F}_m$
, if it has a classifying space with finite m-skeleton. When
$\mathrm {F}_m$
, if it has a classifying space with finite m-skeleton. When
![]() $m=1$
or 2, being of type
$m=1$
or 2, being of type
![]() $\mathrm {F}_m$
is equivalent to
$\mathrm {F}_m$
is equivalent to
![]() $\Gamma $
being finitely generated or finitely presented, respectively.
$\Gamma $
being finitely generated or finitely presented, respectively.
Corollary 3. In dimension
![]() $n=7,8$
, the lattice
$n=7,8$
, the lattice
![]() $\mathrm {O}(n,1,{\mathbb {Z}})$
contains a finitely presented subgroup
$\mathrm {O}(n,1,{\mathbb {Z}})$
contains a finitely presented subgroup
![]() $\Gamma $
without torsion and with infinite Betti number
$\Gamma $
without torsion and with infinite Betti number
![]() $b_{n-1}(\Gamma )$
. In particular,
$b_{n-1}(\Gamma )$
. In particular,
![]() $\Gamma $
is
$\Gamma $
is
![]() $\mathrm { F}_2$
but not
$\mathrm { F}_2$
but not
![]() $\mathrm {F}_{n-1}$
.
$\mathrm {F}_{n-1}$
.
Proof. Pick
![]() $\Gamma = \pi _1(\widetilde M^n) < \pi _1(M^n) < \mathrm {O}(n,1,{\mathbb {Z}})$
. Since
$\Gamma = \pi _1(\widetilde M^n) < \pi _1(M^n) < \mathrm {O}(n,1,{\mathbb {Z}})$
. Since
![]() $\widetilde M^n$
has infinitely many cusps of maximal rank, it is homeomorphic to the interior of a manifold with infinitely many compact boundary components and, hence, has infinite Betti number
$\widetilde M^n$
has infinitely many cusps of maximal rank, it is homeomorphic to the interior of a manifold with infinitely many compact boundary components and, hence, has infinite Betti number
![]() $b_{n-1}(\widetilde M^n) = b_{n-1}(\Gamma )$
.
$b_{n-1}(\widetilde M^n) = b_{n-1}(\Gamma )$
.
For every
![]() $5\leq n \leq 8$
, all the finitely many cusps of
$5\leq n \leq 8$
, all the finitely many cusps of
![]() $M^n$
are toric, that is diffeomorphic to
$M^n$
are toric, that is diffeomorphic to
![]() $T^{n-1}\times [0,+\infty )$
, where we use
$T^{n-1}\times [0,+\infty )$
, where we use
![]() $T^m$
to denote the m-torus. The cover
$T^m$
to denote the m-torus. The cover
![]() $\widetilde M^n$
has infinitely many toric cusps, and finitely many cusps of rank
$\widetilde M^n$
has infinitely many toric cusps, and finitely many cusps of rank
![]() $n-2$
, each diffeomorphic to
$n-2$
, each diffeomorphic to
![]() $T^{n-2} \times {\mathbb {R}} \times [0, +\infty )$
.
$T^{n-2} \times {\mathbb {R}} \times [0, +\infty )$
.
The manifolds
![]() $M^n$
and the maps f are constructed explicitly and combinatorially, so some topological invariants may be calculated. The Euler characteristic, Betti numbers and number of cusps of
$M^n$
and the maps f are constructed explicitly and combinatorially, so some topological invariants may be calculated. The Euler characteristic, Betti numbers and number of cusps of
![]() $M^n$
are listed in Table 1.
$M^n$
are listed in Table 1.
Table 1 The Euler characteristic, Betti numbers and the number of cusps of each hyperbolic n-manifold
![]() $M^n$
. Each cusp of
$M^n$
. Each cusp of
![]() $M^n$
is toric, that is diffeomorphic to
$M^n$
is toric, that is diffeomorphic to
![]() $T^{n-1} \times [0, +\infty )$
.
$T^{n-1} \times [0, +\infty )$
.

Outline of the construction
We use as building blocks a remarkable sequence of finite-volume right-angled polytopes
![]() $P^n \subset {\mathbb {H}}^n$
, defined for
$P^n \subset {\mathbb {H}}^n$
, defined for
![]() $3\leq n \leq 8$
. The reflection group of
$3\leq n \leq 8$
. The reflection group of
![]() $P^n$
is a finite-index subgroup of the integral lattice
$P^n$
is a finite-index subgroup of the integral lattice
![]() $\mathrm {O}(n, 1, {\mathbb {Z}})$
. The polytope
$\mathrm {O}(n, 1, {\mathbb {Z}})$
. The polytope
![]() $P^n$
has both ideal and real vertices.
$P^n$
has both ideal and real vertices.
These polytopes made their first appearance in a paper of Agol, Long and Reid [Reference Agol, Long and Reid1]. Their combinatorics was then described by Potyagailo and Vinberg [Reference Potyagailo and Vinberg30], and more information was later collected by Everitt, Ratcliffe and Tschantz [Reference Everitt, Ratcliffe and Tschantz14], who noticed, in particular, that
![]() $P^3, \ldots , P^8$
are combinatorially dual to the Euclidean Gosset polytopes [Reference Gosset16] discovered by Gosset in 1900 and usually indicated with the symbols
$P^3, \ldots , P^8$
are combinatorially dual to the Euclidean Gosset polytopes [Reference Gosset16] discovered by Gosset in 1900 and usually indicated with the symbols
![]() $-1_{21}, 0_{21}, \ldots , 4_{21}$
.
$-1_{21}, 0_{21}, \ldots , 4_{21}$
.
The Gosset polytopes form indeed a remarkable family of semiregular polytopes. The 1-skeleton of
![]() $2_{21}$
is the configuration graph of the 27 lines in a generic cubic [Reference Coxeter11], while
$2_{21}$
is the configuration graph of the 27 lines in a generic cubic [Reference Coxeter11], while
![]() $3_{21}, 4_{21}$
are intimately connected with the integral octonions and the
$3_{21}, 4_{21}$
are intimately connected with the integral octonions and the
![]() $E_8$
lattice. It has been a great pleasure to study these beautiful objects for this project.
$E_8$
lattice. It has been a great pleasure to study these beautiful objects for this project.
The hyperbolic manifold
![]() $M^n$
is constructed by assembling some copies of
$M^n$
is constructed by assembling some copies of
![]() $P^n$
by means of a suitable colouring of its facets. This is a standard procedure that works with any right-angled polytope and was used (with a different language) by Löbell in 1930 with the right-angled dodecahedron to build the first compact hyperbolic 3-manifold (see [Reference Vesnin38]). For our purposes here, it is important to find a colouring with few colours and many symmetries. Given the remarkable properties of the dual Gosset polytopes, it is natural to guess that some nice symmetric colourings for
$P^n$
by means of a suitable colouring of its facets. This is a standard procedure that works with any right-angled polytope and was used (with a different language) by Löbell in 1930 with the right-angled dodecahedron to build the first compact hyperbolic 3-manifold (see [Reference Vesnin38]). For our purposes here, it is important to find a colouring with few colours and many symmetries. Given the remarkable properties of the dual Gosset polytopes, it is natural to guess that some nice symmetric colourings for
![]() $P^n$
should exist, and we show here that this is indeed the case. In dimension
$P^n$
should exist, and we show here that this is indeed the case. In dimension
![]() $n=7,8$
, we derive a natural colouring from the algebraic properties of the integral octonions.
$n=7,8$
, we derive a natural colouring from the algebraic properties of the integral octonions.
Having constructed
![]() $M^n$
, we build a map
$M^n$
, we build a map
![]() $f\colon M^n \to S^1$
by choosing an appropriate state for
$f\colon M^n \to S^1$
by choosing an appropriate state for
![]() $P^n$
that is a partition of its facets into two sets, In and Out. A state defines a diagonal map
$P^n$
that is a partition of its facets into two sets, In and Out. A state defines a diagonal map
![]() $f\colon M^n \to S^1$
, as explained by Jankiewicz, Norin and Wise [Reference Jankiewicz, Norin and Wise18]. The homomorphism
$f\colon M^n \to S^1$
, as explained by Jankiewicz, Norin and Wise [Reference Jankiewicz, Norin and Wise18]. The homomorphism
![]() $f_*\colon \pi _1(M^n) \to {\mathbb {Z}}$
is often nontrivial, and its kernel may be studied through the Bestvina-Brady theory of combinatorial Morse functions [Reference Bestvina and Brady7]. This fundamental paper furnishes, in particular, some conditions that, when satisfied, guarantee that
$f_*\colon \pi _1(M^n) \to {\mathbb {Z}}$
is often nontrivial, and its kernel may be studied through the Bestvina-Brady theory of combinatorial Morse functions [Reference Bestvina and Brady7]. This fundamental paper furnishes, in particular, some conditions that, when satisfied, guarantee that
![]() $\ker f_*$
is finitely generated or, even better, finitely presented. The conditions are the following: If some simplicial complexes called ascending and descending links are all connected (respectively, simply connected), then the kernel is finitely generated (respectively, finitely presented).
$\ker f_*$
is finitely generated or, even better, finitely presented. The conditions are the following: If some simplicial complexes called ascending and descending links are all connected (respectively, simply connected), then the kernel is finitely generated (respectively, finitely presented).
The choice of an appropriate state for
![]() $P^n$
is crucial here, and we have used again the exceptional properties of the dual Gosset polytope, and of the integral octonions for
$P^n$
is crucial here, and we have used again the exceptional properties of the dual Gosset polytope, and of the integral octonions for
![]() $n=7,8$
, to select a particularly symmetric state for which the abovementioned conditions are satisfied. We took inspiration from a quaternions-generated state for the 24-cell that worked very well in [Reference Battista and Martelli6] to design a similar octonions-generated state for
$n=7,8$
, to select a particularly symmetric state for which the abovementioned conditions are satisfied. We took inspiration from a quaternions-generated state for the 24-cell that worked very well in [Reference Battista and Martelli6] to design a similar octonions-generated state for
![]() $P^7$
and
$P^7$
and
![]() $P^8$
here.
$P^8$
here.
After choosing the states, the conditions on the ascending and descending links have been verified by hand in the lower dimensions
![]() $n=3,4,5$
and with a computer code written in Sage in the higher dimensions
$n=3,4,5$
and with a computer code written in Sage in the higher dimensions
![]() $n=6,7,8$
. The code may be downloaded from [Reference Martelli39]. The symmetries of the polytopes, of the colourings and of the states have reduced considerably the computations involved, to keep them within few hours of process time. Without all these exceptional symmetries, not only the proof of Theorem 1, but even the more straightforward calculation of the Betti numbers of
$n=6,7,8$
. The code may be downloaded from [Reference Martelli39]. The symmetries of the polytopes, of the colourings and of the states have reduced considerably the computations involved, to keep them within few hours of process time. Without all these exceptional symmetries, not only the proof of Theorem 1, but even the more straightforward calculation of the Betti numbers of
![]() $M^n$
would have been problematic. This is especially in the higher dimensions
$M^n$
would have been problematic. This is especially in the higher dimensions
![]() $n=7,8$
, where the combinatorics is highly not trivial, as one can guess by looking at the size of the numbers in Table 1. To the best of our knowledge, the manifolds
$n=7,8$
, where the combinatorics is highly not trivial, as one can guess by looking at the size of the numbers in Table 1. To the best of our knowledge, the manifolds
![]() $M^7$
and
$M^7$
and
![]() $M^8$
are the first finite-volume hyperbolic manifolds in dimension
$M^8$
are the first finite-volume hyperbolic manifolds in dimension
![]() $n\geq 7$
for which the Betti numbers have been computed. Some notable examples exist in the literature in dimension 5 and 6 (see [Reference Everitt, Ratcliffe and Tschantz14, 33]). The cover
$n\geq 7$
for which the Betti numbers have been computed. Some notable examples exist in the literature in dimension 5 and 6 (see [Reference Everitt, Ratcliffe and Tschantz14, 33]). The cover
![]() $\widetilde M^n = {\mathbb {H}}^n/{\ker f_*}$
has a finitely generated fundamental group, and also a finitely presented one for
$\widetilde M^n = {\mathbb {H}}^n/{\ker f_*}$
has a finitely generated fundamental group, and also a finitely presented one for
![]() $n=7,8$
. It has infinitely many cusps for all
$n=7,8$
. It has infinitely many cusps for all
![]() $5\leq n \leq 8$
because f is homotopically trivial on some cusp of
$5\leq n \leq 8$
because f is homotopically trivial on some cusp of
![]() $M^n$
, which, therefore, lifts to infinitely many copies of itself in
$M^n$
, which, therefore, lifts to infinitely many copies of itself in
![]() $\widetilde M^n$
.
$\widetilde M^n$
.
Related work
We briefly discuss some works related to the present paper.
Coherence
The fundamental group of a hyperbolic
![]() $3$
-manifold M satisfies a number of nice properties (see [Reference Aschenbrenner, Friedl and Wilton4] for a widely comprehensive discussion). In particular, Scott proved in [Reference Scott35] that
$3$
-manifold M satisfies a number of nice properties (see [Reference Aschenbrenner, Friedl and Wilton4] for a widely comprehensive discussion). In particular, Scott proved in [Reference Scott35] that
![]() $\pi _1(M)$
is coherent: every finitely generated subgroup is also finitely presented.
$\pi _1(M)$
is coherent: every finitely generated subgroup is also finitely presented.
This is not the case in higher dimensions, as first experienced by Kapovich and Potyagailo [Reference Kapovich and Potyagailo22], who constructed in 1991, a geometrically finite hyperbolic 4-manifold with noncoherent fundamental group (see also [Reference Kapovich and Potyagailo23, Reference Potyagailo29]). A compact example was then built by Bowditch and Mess [Reference Bowditch and Mess8] in 1994. Later on, Kapovich, Potyagailo and Vinberg [Reference Kapovich, Potyagailo and Vinberg24] proved noncoherence for every nonuniform arithmetic lattice in
![]() $\mathrm {Isom}( {\mathbb {H}}^n)$
with
$\mathrm {Isom}( {\mathbb {H}}^n)$
with
![]() $n\geq 6$
, and then Kapovich [Reference Kapovich21] for every arithmetic hyperbolic lattice in dimension
$n\geq 6$
, and then Kapovich [Reference Kapovich21] for every arithmetic hyperbolic lattice in dimension
![]() $n\geq 5, n\neq 7$
. He also conjectured in [Reference Kapovich21] that every hyperbolic lattice in dimension
$n\geq 5, n\neq 7$
. He also conjectured in [Reference Kapovich21] that every hyperbolic lattice in dimension
![]() $n\geq 4$
should be noncoherent.
$n\geq 4$
should be noncoherent.
Corollaries 2 and 3 describe an even wilder situation: In dimension
![]() $n=7,8$
there are finite-volume hyperbolic n-manifolds whose fundamental group contains subgroups that are
$n=7,8$
there are finite-volume hyperbolic n-manifolds whose fundamental group contains subgroups that are
![]() $\mathrm {F}_2$
but not
$\mathrm {F}_2$
but not
![]() $\mathrm {F}_{n-1}$
. The first example of a group that is
$\mathrm {F}_{n-1}$
. The first example of a group that is
![]() $\mathrm {F}_2$
but not
$\mathrm {F}_2$
but not
![]() $\mathrm {F}_m$
for some
$\mathrm {F}_m$
for some
![]() $m\geq 3$
was provided by Stallings [Reference Stallings37]. It would be interesting to know if such subgroups may also occur in the intermediate dimensions
$m\geq 3$
was provided by Stallings [Reference Stallings37]. It would be interesting to know if such subgroups may also occur in the intermediate dimensions
![]() $n=4,5,6$
.
$n=4,5,6$
.
Algebraic fibrations
Theorem 1 furnishes some explicit examples of algebraically fibring fundamental groups of hyperbolic manifolds. We recall that a group G fibres algebraically if there is a surjective homomorphism
![]() $G \to {\mathbb {Z}}$
with finitely generated kernel.
$G \to {\mathbb {Z}}$
with finitely generated kernel.
When
![]() $G= \pi _1(M)$
is the fundamental group of a 3-manifold, by a well-known theorem of Stallings [Reference Stallings36], this condition is equivalent to the existence of a fibration
$G= \pi _1(M)$
is the fundamental group of a 3-manifold, by a well-known theorem of Stallings [Reference Stallings36], this condition is equivalent to the existence of a fibration
![]() $M\to S^1$
. In higher dimensions this is false in general, and the first examples of algebraic fibrations on hyperbolic n-manifolds have appeared recently in dimension
$M\to S^1$
. In higher dimensions this is false in general, and the first examples of algebraic fibrations on hyperbolic n-manifolds have appeared recently in dimension
![]() $n=4$
in [Reference Agol and Stover2, Reference Jankiewicz, Norin and Wise18]. The paper [Reference Jankiewicz, Norin and Wise18] is the main inspiration for our work. In [Reference Agol and Stover2], the algebraic fibration is obtained by constructing a residually finite rational solvable (RFRS) tower and then applying a recent general theorem of Kielak [Reference Kielak25] that transforms the RFRS property into an algebraic fibration (under some hypothesis).
$n=4$
in [Reference Agol and Stover2, Reference Jankiewicz, Norin and Wise18]. The paper [Reference Jankiewicz, Norin and Wise18] is the main inspiration for our work. In [Reference Agol and Stover2], the algebraic fibration is obtained by constructing a residually finite rational solvable (RFRS) tower and then applying a recent general theorem of Kielak [Reference Kielak25] that transforms the RFRS property into an algebraic fibration (under some hypothesis).
Perfect circle-valued Morse functions
In dimension 4, the algebraic fibration can sometimes be promoted to a perfect circle-valued Morse function [Reference Battista and Martelli6]. The algebraic fibrations constructed here in dimension
![]() $5\leq n \leq 8$
cannot be promoted to perfect circle-valued Morse functions because they are homotopically trivial on some cusps (see Section 2.14). After writing a first draft of this paper, we could modify the construction in dimension
$5\leq n \leq 8$
cannot be promoted to perfect circle-valued Morse functions because they are homotopically trivial on some cusps (see Section 2.14). After writing a first draft of this paper, we could modify the construction in dimension
![]() $n=5$
to build a fibration [Reference Italiano, Martelli and Migliorini17].
$n=5$
to build a fibration [Reference Italiano, Martelli and Migliorini17].
Infinitely many cusps
Theorem 1 produces some hyperbolic manifolds with finitely presented fundamental group and infinitely many cusps.
In dimension 3, every hyperbolic manifold with finitely generated fundamental group has only finitely many cusps. This is yet another nice property of 3-manifolds that fails in higher dimensions: We already know from [Reference Kapovich19, Reference Kapovich and Potyagailo22] that there are some hyperbolic 4-manifolds with finitely generated fundamental group and infinitely many rank-1 cusps. With Theorem 1, we upgrade these examples by substituting ‘rank-1’ with ‘maximal rank’ and ‘finitely generated’ with ‘finitely presented’. The reader may consult [Reference Kapovich20] for a comprehensive survey on 3-dimensional theorems that are not valid in higher dimension (the paper also contains a lot of interesting material).
It is conjectured in [Reference Kapovich19] that there is no hyperbolic n-manifold with finitely generated fundamental group and infinitely many cusps, all of maximal rank. We note that Theorem 1 does not disprove this conjecture, since
![]() $\widetilde M^n$
also contains finitely many cusps of rank
$\widetilde M^n$
also contains finitely many cusps of rank
![]() $n-2$
.
$n-2$
.
Structure of the paper
We introduce the polytopes
![]() $P^n$
and construct the manifolds
$P^n$
and construct the manifolds
![]() $M^n$
in Section 1 by means of some appropriate colourings. Then in Section 2, we introduce the techniques of [Reference Jankiewicz, Norin and Wise18] and build the diagonal maps
$M^n$
in Section 1 by means of some appropriate colourings. Then in Section 2, we introduce the techniques of [Reference Jankiewicz, Norin and Wise18] and build the diagonal maps
![]() $f \colon M^n \to S^1$
via some carefully chosen states. By analysing the behaviour of f, we finally prove Theorem 1.
$f \colon M^n \to S^1$
via some carefully chosen states. By analysing the behaviour of f, we finally prove Theorem 1.
1 The manifolds
 $M^n$
$M^n$
We recall a general procedure to construct a manifold from a right-angled polytope P by colouring its facets. This method was first introduced by Vesnin [Reference Vesnin38] in 1987, inspired by the 1931 construction of Löbell of the first known compact hyperbolic 3-manifold [Reference Löbell28] and by a paper of Al Jubouri [Reference Al Jubouri3]. The method was then applied in dimension 4 by Bowditch and Mess [Reference Bowditch and Mess8], and more recently by various authors, including Kolpakov and Martelli [Reference Kolpakov and Martelli26] and Kolpakov and Slavich [Reference Kolpakov and Slavich27].
After recalling some general facts, we turn to the polytopes
![]() $P^3,\ldots , P^8$
and choose some nice colouring to generate the manifolds
$P^3,\ldots , P^8$
and choose some nice colouring to generate the manifolds
![]() $M^3, \ldots , M^8$
. We will use the algebraic properties of the octonions to build
$M^3, \ldots , M^8$
. We will use the algebraic properties of the octonions to build
![]() $M^7$
and
$M^7$
and
![]() $M^8$
.
$M^8$
.
1.1 Colours
Let
![]() $P\subset {\mathbb {X}}^n$
be a right-angled finite polytope in some space
$P\subset {\mathbb {X}}^n$
be a right-angled finite polytope in some space
![]() $ {\mathbb {X}}^n = {\mathbb {H}}^n, {\mathbb {R}}^n$
or
$ {\mathbb {X}}^n = {\mathbb {H}}^n, {\mathbb {R}}^n$
or
![]() $ {\mathbb {S}}^n$
. We always suppose that P has finite volume. When
$ {\mathbb {S}}^n$
. We always suppose that P has finite volume. When
![]() $ {\mathbb {X}}^n = {\mathbb {H}}^n$
, the polytope P may have both finite and ideal vertices. We can interpret P as an orbifold
$ {\mathbb {X}}^n = {\mathbb {H}}^n$
, the polytope P may have both finite and ideal vertices. We can interpret P as an orbifold
![]() $P= {\mathbb {X}}^n /\Gamma $
, where
$P= {\mathbb {X}}^n /\Gamma $
, where
![]() $\Gamma $
is the right-angled Coxeter group generated by the reflections
$\Gamma $
is the right-angled Coxeter group generated by the reflections
![]() $r_F$
along the facets F of P. A presentation for
$r_F$
along the facets F of P. A presentation for
![]() $\Gamma $
is
$\Gamma $
is
where F varies among the facets of P and
![]() $F,F'$
among the pairs of adjacent facets.
$F,F'$
among the pairs of adjacent facets.
A c-colouring of P is the assignment of a colour (taken from some fixed set of c elements) to each facet of P, such that incident facets have distinct colours. We generally use
![]() $\{1,\ldots , c\}$
as a palette of colours and suppose that every colour is painted on at least one facet.
$\{1,\ldots , c\}$
as a palette of colours and suppose that every colour is painted on at least one facet.
Let
![]() $e_1,\ldots , e_c$
be the canonical basis of the
$e_1,\ldots , e_c$
be the canonical basis of the
![]() ${\mathbb {Z}}_2$
-vector space
${\mathbb {Z}}_2$
-vector space
![]() ${\mathbb {Z}}_2^c$
. A colouring on P induces a homomorphism
${\mathbb {Z}}_2^c$
. A colouring on P induces a homomorphism
![]() $\Gamma \to {\mathbb {Z}}_2^c$
that sends
$\Gamma \to {\mathbb {Z}}_2^c$
that sends
![]() $r_F$
of to
$r_F$
of to
![]() $e_j$
, where j is the colour of F. One verifies that the kernel
$e_j$
, where j is the colour of F. One verifies that the kernel
![]() $\Gamma ' \triangleleft \Gamma $
acts freely on
$\Gamma ' \triangleleft \Gamma $
acts freely on
![]() $ {\mathbb {X}}^n$
, and, hence, we get a manifold
$ {\mathbb {X}}^n$
, and, hence, we get a manifold
![]() $M= {\mathbb {X}}^n/{\Gamma '}$
that orbifold-covers
$M= {\mathbb {X}}^n/{\Gamma '}$
that orbifold-covers
![]() $P= {\mathbb {X}}^n/\Gamma $
with degree
$P= {\mathbb {X}}^n/\Gamma $
with degree
![]() $2^c$
.
$2^c$
.
Remark 4. A more general notion of colouring consists of assigning a vector
![]() $\lambda _F \in {\mathbb {Z}}_2^c$
to each facet F of P, that is not necessarily a member of the canonical basis. We require that facets with nonempty intersection are sent to independent vectors (see, for instance, [Reference Kolpakov and Slavich27]). We do not need this more general definition here.
$\lambda _F \in {\mathbb {Z}}_2^c$
to each facet F of P, that is not necessarily a member of the canonical basis. We require that facets with nonempty intersection are sent to independent vectors (see, for instance, [Reference Kolpakov and Slavich27]). We do not need this more general definition here.
The manifold
![]() $M= {\mathbb {X}}^n/\Gamma '$
is hyperbolic, flat or elliptic, according to the model
$M= {\mathbb {X}}^n/\Gamma '$
is hyperbolic, flat or elliptic, according to the model
![]() $ {\mathbb {X}}^n$
, and is tessellated into
$ {\mathbb {X}}^n$
, and is tessellated into
![]() $2^c$
copies of P. Geometrically, we may see M as constructed by mirroring P iteratively along facets sharing the same colours
$2^c$
copies of P. Geometrically, we may see M as constructed by mirroring P iteratively along facets sharing the same colours
![]() $1,\ldots , c$
.
$1,\ldots , c$
.
More precisely, we can describe the tessellation of M into
![]() $2^c$
copies of P as follows. For every vector
$2^c$
copies of P as follows. For every vector
![]() $v\in {\mathbb {Z}}_2^c$
, we denote by
$v\in {\mathbb {Z}}_2^c$
, we denote by
![]() $P_v$
an identical copy of P. We identify each facet F of
$P_v$
an identical copy of P. We identify each facet F of
![]() $P_v$
via the identity map with the same facet of
$P_v$
via the identity map with the same facet of
![]() $P_{v+e_j}$
, where j is the colour of F. This gives the tessellation of M.
$P_{v+e_j}$
, where j is the colour of F. This gives the tessellation of M.
We say that two colourings on P are isomorphic if they induce the same partition of facets, possibly after acting by some isometry of P. Isomorphic colourings yield isometric manifolds M.
As an example, we can always colour P by assigning distinct colours to distinct facets. In this case, c equals the number of facets of P and
![]() $\Gamma \to {\mathbb {Z}}_2^c$
is just the abelianisation homomorphism. With this choice, the resulting manifold M can be quite big and often intractable (especially in higher dimension
$\Gamma \to {\mathbb {Z}}_2^c$
is just the abelianisation homomorphism. With this choice, the resulting manifold M can be quite big and often intractable (especially in higher dimension
![]() $n>3$
), so it is often preferable to work with a small number of colours. Another fundamental reason for rejecting this inefficient colouring will be given below in Corollary 13.
$n>3$
), so it is often preferable to work with a small number of colours. Another fundamental reason for rejecting this inefficient colouring will be given below in Corollary 13.
Here are some more interesting examples:
-
• The Euclidean n-cube has a unique n-colouring up to isomorphisms, where opposite facets are coloured with the same colour. This colouring produces a flat torus tessellated into
 $2^n$
cubes. The case
$2^n$
cubes. The case
 $n=2$
is shown in Figure 1 and is easily generalised to any n. More generally, we will prove below that any colouring on the n-cube produces a flat torus.
$n=2$
is shown in Figure 1 and is easily generalised to any n. More generally, we will prove below that any colouring on the n-cube produces a flat torus.
Figure 1 A square P with two colours (left). The flat manifold M is constructed by taking four copies of P and identifying the edges as shown (centre). We get a flat square torus (right).
-
• The right-angled spherical n-simplex has a unique colouring up to isomorphisms: It has
 $n+1$
colours, and it produces the spherical manifold
$n+1$
colours, and it produces the spherical manifold
 $S^n$
with its standard tessellation into
$S^n$
with its standard tessellation into
 $2^{n+1}$
right-angled simplexes.
$2^{n+1}$
right-angled simplexes. -
• Every ideal hyperbolic polygon is right-angled in a vacuous sense (it has no finite vertices) and can be 1-coloured! Indeed, the edges are pairwise disjoint and, hence, can all be given the same colour. The construction produces the double of the polygon, a hyperbolic punctured sphere.
-
• Every right-angled hyperbolic hexagon can be 2-coloured, and the result is the double of a geodesic pair-of-pants, that is a genus-2 hyperbolic surface, tessellated into four hexagons.
-
• The ideal octahedron in
 $ {\mathbb {H}}^3$
has a unique 2-colouring up to isomorphisms. The colouring produces a cusped hyperbolic 3-manifold which is the complement of the minimally twisted chain link with six components shown in Figure 2 (see [Reference Kolpakov and Martelli26] for more details).
$ {\mathbb {H}}^3$
has a unique 2-colouring up to isomorphisms. The colouring produces a cusped hyperbolic 3-manifold which is the complement of the minimally twisted chain link with six components shown in Figure 2 (see [Reference Kolpakov and Martelli26] for more details).
Figure 2 The minimally twisted chain link with six components.
-
• The ideal 24-cell in
 $ {\mathbb {H}}^4$
has a unique 3-colouring, that produces a hyperbolic 4-manifold with 24 cusps with 3-torus sections (see [Reference Kolpakov and Martelli26]).
$ {\mathbb {H}}^4$
has a unique 3-colouring, that produces a hyperbolic 4-manifold with 24 cusps with 3-torus sections (see [Reference Kolpakov and Martelli26]).
Remark 5. When P is compact, it has some finite vertex incident to n pairwise incident facets. These facets must have distinct colours and, hence, we necessarily have
![]() $c\geq n$
. When
$c\geq n$
. When
![]() $c=n$
, the covering
$c=n$
, the covering
![]() $M\to P$
has the minimum possible degree and is called a small cover. These were studied in [Reference Davis and Januszkiewicz13]. Our examples will not be small covers because the polytopes that we consider have some ideal vertices, and, moreover, we will often have
$M\to P$
has the minimum possible degree and is called a small cover. These were studied in [Reference Davis and Januszkiewicz13]. Our examples will not be small covers because the polytopes that we consider have some ideal vertices, and, moreover, we will often have
![]() $c>n$
.
$c>n$
.
Remark 6. The manifold M is always orientable: It suffices to orient
![]() $P_v$
like P if and only if
$P_v$
like P if and only if
![]() $v_1+\cdots +v_c$
is even (see an example in Figure 1). We note that M is not guaranteed to be orientable if one uses the more general notion of colouring of Remark 4. The crucial fact here is that all the vectors
$v_1+\cdots +v_c$
is even (see an example in Figure 1). We note that M is not guaranteed to be orientable if one uses the more general notion of colouring of Remark 4. The crucial fact here is that all the vectors
![]() $e_j \in {\mathbb {Z}}_2^c$
colouring the facets have an odd number of 1’s in their entries.
$e_j \in {\mathbb {Z}}_2^c$
colouring the facets have an odd number of 1’s in their entries.
1.2 Cusp sections
When
![]() $P\subset {\mathbb {H}}^n$
has some ideal vertex, the resulting manifold M has some cusps, and there is a simple and straightforward procedure to derive its shape directly from the combinatorics of P and its colouring, that we now explain.
$P\subset {\mathbb {H}}^n$
has some ideal vertex, the resulting manifold M has some cusps, and there is a simple and straightforward procedure to derive its shape directly from the combinatorics of P and its colouring, that we now explain.
Let v be an ideal vertex of
![]() $P\subset {\mathbb {H}}^n$
. The link of v in P is by definition the intersection of P with a small horosphere centered at v. It is a right-angled Euclidean
$P\subset {\mathbb {H}}^n$
. The link of v in P is by definition the intersection of P with a small horosphere centered at v. It is a right-angled Euclidean
![]() $(n-1)$
-parallelepiped C. We use the letter C because a parallelepiped is combinatorially a cube, and, in fact, it will also be isometric to a cube in all the cases that are of interest here.
$(n-1)$
-parallelepiped C. We use the letter C because a parallelepiped is combinatorially a cube, and, in fact, it will also be isometric to a cube in all the cases that are of interest here.
The parallelepiped C inherits a colouring from that of P: it suffices to assign to every
![]() $(n-2)$
-facet of C the colour of the
$(n-2)$
-facet of C the colour of the
![]() $(n-1)$
-facet of P that contains it. The induced colouring on C generates an abstract compact flat
$(n-1)$
-facet of P that contains it. The induced colouring on C generates an abstract compact flat
![]() $(n-1)$
-manifold N that orbifold-covers C by the procedure explained above. The manifold N is tessellated into
$(n-1)$
-manifold N that orbifold-covers C by the procedure explained above. The manifold N is tessellated into
![]() $2^{c'}$
copies of C, where
$2^{c'}$
copies of C, where
![]() $c'\leq c$
is the number of colours of C.
$c'\leq c$
is the number of colours of C.
By construction, the preimage of C in M consists of some copies of N. The number of copies is equal to
![]() $2^h$
, where
$2^h$
, where
![]() $h=c-c'$
is the number of colours in
$h=c-c'$
is the number of colours in
![]() $\{1,\ldots , c\}$
that are not assigned to any facet incident to v, that is that are not assigned to any facet of C. The preimage of C in M consists of
$\{1,\ldots , c\}$
that are not assigned to any facet incident to v, that is that are not assigned to any facet of C. The preimage of C in M consists of
![]() $2^c = 2^h \cdot 2^{c'}$
copies of C in total.
$2^c = 2^h \cdot 2^{c'}$
copies of C in total.
Summing up: There are
![]() $2^h$
cusps in M lying above v, each with section N derived directly from C and its induced colouring. Here are some examples:
$2^h$
cusps in M lying above v, each with section N derived directly from C and its induced colouring. Here are some examples:
-
• If
 $P\subset {\mathbb {H}}^2$
is a 1-coloured ideal polygon, the link C at each ideal vertex v is a 1-coloured 1-cube (that is, a segment). Here,
$P\subset {\mathbb {H}}^2$
is a 1-coloured ideal polygon, the link C at each ideal vertex v is a 1-coloured 1-cube (that is, a segment). Here,
 $h=0$
, the preimage of C is a circle and there is one cusp above each v. The punctured sphere M has one cusp above each ideal vertex of P.
$h=0$
, the preimage of C is a circle and there is one cusp above each v. The punctured sphere M has one cusp above each ideal vertex of P. -
• If
 $P\subset {\mathbb {H}}^2$
is a 2-coloured ideal triangle, there are two types of ideal vertices. Two ideal vertices have a 2-coloured 1-cube as a link C, while the third ideal vertex has a 1-coloured 1-cube C. We have
$P\subset {\mathbb {H}}^2$
is a 2-coloured ideal triangle, there are two types of ideal vertices. Two ideal vertices have a 2-coloured 1-cube as a link C, while the third ideal vertex has a 1-coloured 1-cube C. We have
 $h=0$
for the first two ideal vertices, and
$h=0$
for the first two ideal vertices, and
 $h=1$
for the third. Therefore, the counterimage of C consists of one circle for each of the first two ideal vertices and two circles for the third. The manifold M has four cusps overall, two above the first two vertices and two above the third. It is a four-punctured sphere tessellated into four copies of P (see Figure 3).
$h=1$
for the third. Therefore, the counterimage of C consists of one circle for each of the first two ideal vertices and two circles for the third. The manifold M has four cusps overall, two above the first two vertices and two above the third. It is a four-punctured sphere tessellated into four copies of P (see Figure 3).
Figure 3 When P is an ideal triangle with one or two colours, the manifold M is a sphere with three or four punctures, respectively.
-
• If P is a 2-coloured ideal octahedron, it has six ideal vertices, and the link of each is a 2-coloured square C. We have
 $h=0$
on each ideal vertex, so the counterimage of C in M is a unique torus. The hyperbolic 3-manifold M has six cusps overall, one above each ideal vertex of P. As already stated, M is the complement of the link in Figure 2.
$h=0$
on each ideal vertex, so the counterimage of C in M is a unique torus. The hyperbolic 3-manifold M has six cusps overall, one above each ideal vertex of P. As already stated, M is the complement of the link in Figure 2. -
• If P is a 3-coloured ideal 24-cell in
 $ {\mathbb {H}}^4$
, it has 24 ideal vertices, and the section of each is a 3-coloured 3-cube C (see [Reference Kolpakov and Martelli26]). We have
$ {\mathbb {H}}^4$
, it has 24 ideal vertices, and the section of each is a 3-coloured 3-cube C (see [Reference Kolpakov and Martelli26]). We have
 $h=0$
on each ideal vertex, so the counterimage of C is a single 3-torus. The hyperbolic 4-manifold M has 24 toric cusps, one above each ideal vertex of P.
$h=0$
on each ideal vertex, so the counterimage of C is a single 3-torus. The hyperbolic 4-manifold M has 24 toric cusps, one above each ideal vertex of P.
1.3 The Euclidean parallelepiped
One basic example is the Euclidean right-angled n-parallelepiped
Fix a c-colouring of C. Only opposite facets are disjoint and, hence, may share the same colour. Therefore, we have
![]() $n \leq c \leq 2n$
, there are
$n \leq c \leq 2n$
, there are
![]() $2n-c$
pairs of opposite facets with the same colour and the remaining
$2n-c$
pairs of opposite facets with the same colour and the remaining
![]() $2(c-n)$
facets with distinct colours. Let M be the flat manifold produced by the c-colouring of C.
$2(c-n)$
facets with distinct colours. Let M be the flat manifold produced by the c-colouring of C.
Proposition 7. The resulting flat manifold M is an n-torus isometric to a product of circles of lengths
![]() $a_1l_1, \ldots , a_nl_n$
. Here,
$a_1l_1, \ldots , a_nl_n$
. Here,
![]() $a_i$
equals 2 or 4 depending on whether the i-th pair of opposite facets share the same colour or not.
$a_i$
equals 2 or 4 depending on whether the i-th pair of opposite facets share the same colour or not.
Proof. Recall that
![]() $M = {\mathbb {R}}^n/\Gamma '$
, where
$M = {\mathbb {R}}^n/\Gamma '$
, where
![]() $\Gamma $
is the reflection group of C and
$\Gamma $
is the reflection group of C and
![]() $\Gamma '\triangleleft \Gamma $
is the kernel of the map
$\Gamma '\triangleleft \Gamma $
is the kernel of the map
![]() $\Gamma \to {\mathbb {Z}}_2^c$
induced by the colouring.
$\Gamma \to {\mathbb {Z}}_2^c$
induced by the colouring.
Let
![]() $r_{i,1}$
and
$r_{i,1}$
and
![]() $r_{i,2}$
be the reflections along the opposite facets of C that are orthogonal to the i-th axis, for
$r_{i,2}$
be the reflections along the opposite facets of C that are orthogonal to the i-th axis, for
![]() $i=1,\ldots , n$
. The composition
$i=1,\ldots , n$
. The composition
![]() $r_{i,1}r_{i,2}$
is a translation along the axis of distance
$r_{i,1}r_{i,2}$
is a translation along the axis of distance
![]() $2l_i$
. If the facets share the same colour, we have
$2l_i$
. If the facets share the same colour, we have
![]() $r_{i,1}r_{i,2} \in \Gamma '$
, while if they do not, we have
$r_{i,1}r_{i,2} \in \Gamma '$
, while if they do not, we have
![]() $r_{i,1}r_{i,2}r_{i,1}r_{i,2} \in \Gamma '$
. This shows that
$r_{i,1}r_{i,2}r_{i,1}r_{i,2} \in \Gamma '$
. This shows that
where
![]() $a_i$
equals 2 or 4 depending on whether the i-th pair of opposite facets share the same colour. These two subgroups have the same index in
$a_i$
equals 2 or 4 depending on whether the i-th pair of opposite facets share the same colour. These two subgroups have the same index in
![]() $\Gamma $
since
$\Gamma $
since
Therefore,
![]() $\Gamma ' = a_1l_1 {\mathbb {Z}} \times \cdots \times a_nl_n {\mathbb {Z}}$
and M is as stated.
$\Gamma ' = a_1l_1 {\mathbb {Z}} \times \cdots \times a_nl_n {\mathbb {Z}}$
and M is as stated.
The proof also shows that M is tessellated into
![]() $2^{2n-c} \cdot 4^{c-n} = 2^c$
copies of C. The two extreme cases are the following: If
$2^{2n-c} \cdot 4^{c-n} = 2^c$
copies of C. The two extreme cases are the following: If
![]() $c=n$
, then M is tessellated into
$c=n$
, then M is tessellated into
![]() $2^c$
copies of C, while if
$2^c$
copies of C, while if
![]() $c=2n$
, then M is tessellated into
$c=2n$
, then M is tessellated into
![]() $4^c$
copies.
$4^c$
copies.
A cusp in a hyperbolic n-manifold is toric if its section is a flat
![]() $(n-1)$
-torus. We summarise our discussion as follows.
$(n-1)$
-torus. We summarise our discussion as follows.
Corollary 8. If
![]() $P\subset {\mathbb {H}}^n$
is right-angled with some ideal vertices, every colouring on P produces some hyperbolic n-manifold M whose cusps are all toric.
$P\subset {\mathbb {H}}^n$
is right-angled with some ideal vertices, every colouring on P produces some hyperbolic n-manifold M whose cusps are all toric.
If P has c colours and v is an ideal vertex, there are
![]() $2^{c-c'}$
toric cusps in M above v, where
$2^{c-c'}$
toric cusps in M above v, where
![]() $c'$
is the number of distinctly coloured facets incident to v.
$c'$
is the number of distinctly coloured facets incident to v.
Remark 9. If we use the more general notion of colouring of Remark 4, nontoric cusps may also appear (see, for instance, [Reference Ferrari, Kolpakov and Slavich15]).
1.4 A program in Sage
We have written a general program in Sage, available from [Reference Martelli39], that may be used to study a coloured right-angled polytope P and the resulting manifold M. The program takes as an input the incidence graph of the facets of P and their colouring, and produces as an output some information on P and, more importantly, on M. It calculates, in particular, the Betti numbers of M via the formula stated in [Reference Choi and Park9, Theorem 1.1], also explained in [Reference Ferrari, Kolpakov and Slavich15, Section 2.2], and the number of cusps of M using Corollary 8.
1.5 The right-angled hyperbolic polytopes
We refer to the excellent papers [Reference Everitt, Ratcliffe and Tschantz14] and [Reference Potyagailo and Vinberg30] for an introduction to the sequence of right-angled hyperbolic polytopes
![]() $P^3,\ldots , P^8$
. These have many beautiful properties that we now briefly summarise.
$P^3,\ldots , P^8$
. These have many beautiful properties that we now briefly summarise.
Each
![]() $P^n \subset {\mathbb {H}}^n$
is a finite volume right-angled polytope with both finite and ideal vertices. The link of a finite or ideal vertex is a right-angled spherical
$P^n \subset {\mathbb {H}}^n$
is a finite volume right-angled polytope with both finite and ideal vertices. The link of a finite or ideal vertex is a right-angled spherical
![]() $(n-1)$
-simplex or a Euclidean
$(n-1)$
-simplex or a Euclidean
![]() $(n-1)$
-cube, respectively. The numbers of facets, ideal vertices and finite vertices of
$(n-1)$
-cube, respectively. The numbers of facets, ideal vertices and finite vertices of
![]() $P^n$
are listed in Table 2, together with the isometry group of
$P^n$
are listed in Table 2, together with the isometry group of
![]() $P^n$
and its order. The isometry group acts transitively on the facets, so, in particular, these are all isometric: In fact, every facet of
$P^n$
and its order. The isometry group acts transitively on the facets, so, in particular, these are all isometric: In fact, every facet of
![]() $P^n$
is isometric to
$P^n$
is isometric to
![]() $P^{n-1}$
when
$P^{n-1}$
when
![]() $n\geq 4$
. The quotient of
$n\geq 4$
. The quotient of
![]() $P^n$
by its isometry group is a simplex.
$P^n$
by its isometry group is a simplex.
Table 2 The number of facets, ideal vertices and finite vertices of
![]() $P^n$
, the isometry group
$P^n$
, the isometry group
![]() $ {\mathrm {Isom}}(P^n)$
expressed as a Weyl group and its order
$ {\mathrm {Isom}}(P^n)$
expressed as a Weyl group and its order
![]() $| {\mathrm {Isom}}(P^n)|$
, and the dual Euclidean polytope.
$| {\mathrm {Isom}}(P^n)|$
, and the dual Euclidean polytope.

1.6 Euler characteristic
Recall that the orbifold Euler characteristic of a hyperbolic right-angled polyhedron P is zero in odd dimension, while in even dimension it can be calculated via the simple formula
 $$ \begin{align*}\chi(P) = \sum_{i=0}^n (-1)^i \frac{f_i}{2^{n-i}},\end{align*} $$
$$ \begin{align*}\chi(P) = \sum_{i=0}^n (-1)^i \frac{f_i}{2^{n-i}},\end{align*} $$
where
![]() $f_i$
is the number of i-dimensional faces of P, including P itself (so
$f_i$
is the number of i-dimensional faces of P, including P itself (so
![]() $f_n=1$
). Only real vertices (not the ideal ones) contribute to
$f_n=1$
). Only real vertices (not the ideal ones) contribute to
![]() $f_0$
. From this formula, we deduce the well-known [Reference Everitt, Ratcliffe and Tschantz14] values
$f_0$
. From this formula, we deduce the well-known [Reference Everitt, Ratcliffe and Tschantz14] values
In even dimension, the Euler characteristic and the volume are roughly the same thing, up to a constant that will be recalled below.
1.7 The dual Gosset polytopes
Combinatorially, the polytopes
![]() $P^n$
are dual to the Gosset polytopes listed in the last column of Table 2 and discovered by Gosset [Reference Gosset16] in 1900 (see [Reference Everitt, Ratcliffe and Tschantz14]). Every Gosset polytope is a Euclidean polytope with regular facets, whose isometry group (which is the same as
$P^n$
are dual to the Gosset polytopes listed in the last column of Table 2 and discovered by Gosset [Reference Gosset16] in 1900 (see [Reference Everitt, Ratcliffe and Tschantz14]). Every Gosset polytope is a Euclidean polytope with regular facets, whose isometry group (which is the same as
![]() $ {\mathrm {Isom}}(P^n)$
) acts transitively on the vertices. The regular facets of the Gosset polytope are of two types: some
$ {\mathrm {Isom}}(P^n)$
) acts transitively on the vertices. The regular facets of the Gosset polytope are of two types: some
![]() $(n-1)$
-simplexes (dual to the real vertices of
$(n-1)$
-simplexes (dual to the real vertices of
![]() $P^n$
) and some
$P^n$
) and some
![]() $(n-1)$
-octahedra (dual to the ideal vertices of
$(n-1)$
-octahedra (dual to the ideal vertices of
![]() $P^n$
). A k-octahedron, here, is the regular polytope dual to the k-cube (sometimes also called k-orthoplex).
$P^n$
). A k-octahedron, here, is the regular polytope dual to the k-cube (sometimes also called k-orthoplex).
We will describe a colouring of
![]() $P^n$
as a colouring of the vertices of the dual Gosset polytope, where we require, of course, that two vertices adjacent connected by an edge must have distinct colours (so only the 1-skeleton of the dual Gosset polytope is important at this stage). We would like to find some colouring with a reasonably small number of colours, and possibly a high degree of symmetry: We are confident that some natural choices should arise from the exceptional properties of
$P^n$
as a colouring of the vertices of the dual Gosset polytope, where we require, of course, that two vertices adjacent connected by an edge must have distinct colours (so only the 1-skeleton of the dual Gosset polytope is important at this stage). We would like to find some colouring with a reasonably small number of colours, and possibly a high degree of symmetry: We are confident that some natural choices should arise from the exceptional properties of
![]() $P^n$
and their dual Gosset polytopes, and this is indeed the case as we will see.
$P^n$
and their dual Gosset polytopes, and this is indeed the case as we will see.
We now analyse the polyhedra
![]() $P^3, \ldots , P^8$
individually. For each
$P^3, \ldots , P^8$
individually. For each
![]() $P^n$
, we define a colouring and study the resulting hyperbolic manifold
$P^n$
, we define a colouring and study the resulting hyperbolic manifold
![]() $M^n$
.
$M^n$
.
1.8 The manifold
 $M^3$
$M^3$
The hyperbolic polyhedron
![]() $P^3\subset {\mathbb {H}}^3$
is the right-angled double pyramid with triangular base shown in Figure 4. The three vertices of the triangular base are ideal, while the two remaining vertices are real. Each of the six faces F of
$P^3\subset {\mathbb {H}}^3$
is the right-angled double pyramid with triangular base shown in Figure 4. The three vertices of the triangular base are ideal, while the two remaining vertices are real. Each of the six faces F of
![]() $P^3$
is a triangle with a right-angled real vertex and two ideal vertices.
$P^3$
is a triangle with a right-angled real vertex and two ideal vertices.

Figure 4 The polyhedron
![]() $P^3$
is a right-angled bipyramid with three ideal vertices along the horizontal plane and two real ones (top and bottom in the figure).
$P^3$
is a right-angled bipyramid with three ideal vertices along the horizontal plane and two real ones (top and bottom in the figure).
The dual Gosset polytope is a triangular prism, whose faces are two base equilateral triangles and three lateral squares. Its 1-skeleton is shown schematically in Figure 5. It can be coloured with three colours in a unique way (shown in the figure) up to isomorphism. Therefore,
![]() $P^3$
has a unique 3-colouring up to isomorphism. The polyhedron cannot be coloured with less than three colours.
$P^3$
has a unique 3-colouring up to isomorphism. The polyhedron cannot be coloured with less than three colours.

Figure 5 The 1-skeleton of the triangular prism has a unique 3-colouring up to isomorphism, shown here.
We equip
![]() $P^3$
with this 3-colouring. This produces a hyperbolic 3-manifold
$P^3$
with this 3-colouring. This produces a hyperbolic 3-manifold
![]() $M^3$
, tessellated into
$M^3$
, tessellated into
![]() $2^3=8$
copies of
$2^3=8$
copies of
![]() $P^3$
.
$P^3$
.
The link of each ideal vertex v of
![]() $P^3$
is a square C, that is dual to a square face of the Gosset prism. We see from Figure 5 that C is 3-coloured: two opposite edges of C have distinct colours, and the other two opposite edges have the same colour. By Corollary 8, the counterimage of C consists of a single (because
$P^3$
is a square C, that is dual to a square face of the Gosset prism. We see from Figure 5 that C is 3-coloured: two opposite edges of C have distinct colours, and the other two opposite edges have the same colour. By Corollary 8, the counterimage of C consists of a single (because
![]() $2^{3-3}=1$
) torus cusp section in
$2^{3-3}=1$
) torus cusp section in
![]() $M^3$
. The hyperbolic manifold
$M^3$
. The hyperbolic manifold
![]() $M^3$
has therefore three cusps, one above each vertex v of P.
$M^3$
has therefore three cusps, one above each vertex v of P.
Using Sage, we have calculated the Betti numbers of
![]() $M^3$
:
$M^3$
:
We get of course,
![]() $\chi (M^3)=0$
.
$\chi (M^3)=0$
.
1.9 The manifold
 $M^4$
$M^4$
The hyperbolic polytope
![]() $P^4\subset {\mathbb {H}}^4$
is fully described in [Reference Potyagailo and Vinberg30, Reference Ratcliffe and Tschantz32], and we refer to these sources for more details. It has 10 facets, each isometric to
$P^4\subset {\mathbb {H}}^4$
is fully described in [Reference Potyagailo and Vinberg30, Reference Ratcliffe and Tschantz32], and we refer to these sources for more details. It has 10 facets, each isometric to
![]() $P^3$
. It has also five real vertices and five ideal vertices.
$P^3$
. It has also five real vertices and five ideal vertices.
The dual Gosset polytope
![]() $0_{21}$
is the 4-dimensional rectified simplex. That is, it is the convex hull of the midpoints of the 10 edges of a regular 4-dimensional simplex. Its 10 vertices may be seen in
$0_{21}$
is the 4-dimensional rectified simplex. That is, it is the convex hull of the midpoints of the 10 edges of a regular 4-dimensional simplex. Its 10 vertices may be seen in
![]() $ {\mathbb {R}}^5$
as the points obtained by permuting the coordinates of
$ {\mathbb {R}}^5$
as the points obtained by permuting the coordinates of
![]() $(0,0,0,1,1)$
. Two such vertices are adjacent if they differ only in two coordinates. The Gosset polytope
$(0,0,0,1,1)$
. Two such vertices are adjacent if they differ only in two coordinates. The Gosset polytope
![]() $0_{21}$
has 10 facets; of these, five are regular tetrahedra (created by the rectification) dual to the finite vertices of
$0_{21}$
has 10 facets; of these, five are regular tetrahedra (created by the rectification) dual to the finite vertices of
![]() $P^4$
, and five are regular octahedra (the rectified facets of the original regular 4-simplex) dual to the ideal vertices of
$P^4$
, and five are regular octahedra (the rectified facets of the original regular 4-simplex) dual to the ideal vertices of
![]() $P^4$
.
$P^4$
.
A convenient orthogonal plane projection of the 1-skeleton of
![]() $0_{21}$
is shown in Figure 6. We assign to
$0_{21}$
is shown in Figure 6. We assign to
![]() $0_{21}$
, and, hence, to
$0_{21}$
, and, hence, to
![]() $P^4$
, the 5-colouring depicted in Figure 7. This produces a hyperbolic 4-manifold
$P^4$
, the 5-colouring depicted in Figure 7. This produces a hyperbolic 4-manifold
![]() $M^4$
, tessellated into
$M^4$
, tessellated into
![]() $2^5 = 32$
copies of
$2^5 = 32$
copies of
![]() $P^4$
. We have
$P^4$
. We have
![]() $\chi (M^4) = 32/16 = 2$
.
$\chi (M^4) = 32/16 = 2$
.

Figure 6 The orthogonal projection of the 1-skeleton of the rectified simplex
![]() $0_{21}$
on the plane in
$0_{21}$
on the plane in
![]() $ {\mathbb {R}}^5$
generated by
$ {\mathbb {R}}^5$
generated by
![]() $(1, \epsilon , -\epsilon , -1, 0)$
and its cyclic permutations, where
$(1, \epsilon , -\epsilon , -1, 0)$
and its cyclic permutations, where
![]() $\epsilon =(\sqrt 5 -1)/2 = 2\cos (2\pi /5)$
is the positive root of
$\epsilon =(\sqrt 5 -1)/2 = 2\cos (2\pi /5)$
is the positive root of
![]() $\epsilon ^2 + \epsilon -1$
. The image of the vertex
$\epsilon ^2 + \epsilon -1$
. The image of the vertex
![]() $(0,0,0,1,1)$
is indicated as
$(0,0,0,1,1)$
is indicated as
![]() $00011$
, and so on. Some edges are superposed along the projection, so two vertices that are connected by an edge on the plane projection may not be so in
$00011$
, and so on. Some edges are superposed along the projection, so two vertices that are connected by an edge on the plane projection may not be so in
![]() $0_{21}$
. To clarify this ambiguity, we have chosen a blue vertex and painted in red the six vertices adjacent to it, in two cases (all the other cases are obtained by rotation).
$0_{21}$
. To clarify this ambiguity, we have chosen a blue vertex and painted in red the six vertices adjacent to it, in two cases (all the other cases are obtained by rotation).

Figure 7 A 5-colouring of the 1-skeleton of
![]() $0_{21}$
and hence of
$0_{21}$
and hence of
![]() $P^4$
.
$P^4$
.
The polytope
![]() $P^4$
has five ideal vertices
$P^4$
has five ideal vertices
![]() $v_1,\ldots , v_5$
. Each
$v_1,\ldots , v_5$
. Each
![]() $v_i$
is dual to the octahedral facet of
$v_i$
is dual to the octahedral facet of
![]() $0_{21}$
contained in the coordinate hyperplane
$0_{21}$
contained in the coordinate hyperplane
![]() $x_i=0$
, whose six vertices in Figure 6 are precisely those with
$x_i=0$
, whose six vertices in Figure 6 are precisely those with
![]() $x_i=0$
. The case
$x_i=0$
. The case
![]() $i=1$
is shown in Figure 8. We can see on the figure that the octahedron is 5-coloured. The other four octahedra are obtained from this one by rotating the plane projection diagram, and they are also 5-coloured.
$i=1$
is shown in Figure 8. We can see on the figure that the octahedron is 5-coloured. The other four octahedra are obtained from this one by rotating the plane projection diagram, and they are also 5-coloured.

Figure 8 An octahedral facet of
![]() $P^4$
. This is a subgraph of the 1-skeleton in Figure 7. Some edges are superposed.
$P^4$
. This is a subgraph of the 1-skeleton in Figure 7. Some edges are superposed.
We have discovered that the link of each ideal vertex of
![]() $P^4$
is a 5-coloured cube C. By Corollary 8, the counterimage of C consists of a single (since
$P^4$
is a 5-coloured cube C. By Corollary 8, the counterimage of C consists of a single (since
![]() $2^{5-5}=1$
) toric cusp section in
$2^{5-5}=1$
) toric cusp section in
![]() $M^4$
. Therefore, the hyperbolic manifold
$M^4$
. Therefore, the hyperbolic manifold
![]() $M^4$
has five cusps overall, one above each ideal vertex of
$M^4$
has five cusps overall, one above each ideal vertex of
![]() $P^4$
.
$P^4$
.
Using Sage, we have calculated the Betti numbers of
![]() $M^4$
:
$M^4$
:
We get
![]() $\chi (M^4)=2$
again.
$\chi (M^4)=2$
again.
1.10 The manifold
 $M^5$
$M^5$
The hyperbolic polytope
![]() $P^5\subset {\mathbb {H}}^5$
is fully described in [Reference Potyagailo and Vinberg30, Reference Ratcliffe and Tschantz33], and we refer to these sources for more details. It has 16 facets, each isometric to
$P^5\subset {\mathbb {H}}^5$
is fully described in [Reference Potyagailo and Vinberg30, Reference Ratcliffe and Tschantz33], and we refer to these sources for more details. It has 16 facets, each isometric to
![]() $P^4$
. It also has 16 real vertices and 10 ideal vertices. Every real vertex is opposed to a facet.
$P^4$
. It also has 16 real vertices and 10 ideal vertices. Every real vertex is opposed to a facet.
The dual Gosset polytope
![]() $1_{21}$
has 16 vertices. We can represent these in
$1_{21}$
has 16 vertices. We can represent these in
![]() $ {\mathbb {R}}^5$
as the vertices
$ {\mathbb {R}}^5$
as the vertices
![]() $(\pm 1, \pm 1, \pm 1, \pm 1, \pm 1)$
with an odd number of minus signs. Two vertices are connected by an edge if they differ only in two coordinates. The Gosset polytope
$(\pm 1, \pm 1, \pm 1, \pm 1, \pm 1)$
with an odd number of minus signs. Two vertices are connected by an edge if they differ only in two coordinates. The Gosset polytope
![]() $1_{21}$
has 26 facets; of these, 16 are regular 4-simplexes dual to the finite vertices of
$1_{21}$
has 26 facets; of these, 16 are regular 4-simplexes dual to the finite vertices of
![]() $P^5$
, and 10 are regular 4-octahedra dual to the ideal vertices of
$P^5$
, and 10 are regular 4-octahedra dual to the ideal vertices of
![]() $P^5$
.
$P^5$
.
A convenient planar projection of its 1-skeleton is shown in Figure 9. We assign to
![]() $1_{21}$
, and, hence, to
$1_{21}$
, and, hence, to
![]() $P^5$
, the 8-colouring depicted in Figure 10. This produces a hyperbolic 5-manifold
$P^5$
, the 8-colouring depicted in Figure 10. This produces a hyperbolic 5-manifold
![]() $M^5$
tessellated into
$M^5$
tessellated into
![]() $2^8 = 256$
copies of
$2^8 = 256$
copies of
![]() $P^5$
.
$P^5$
.
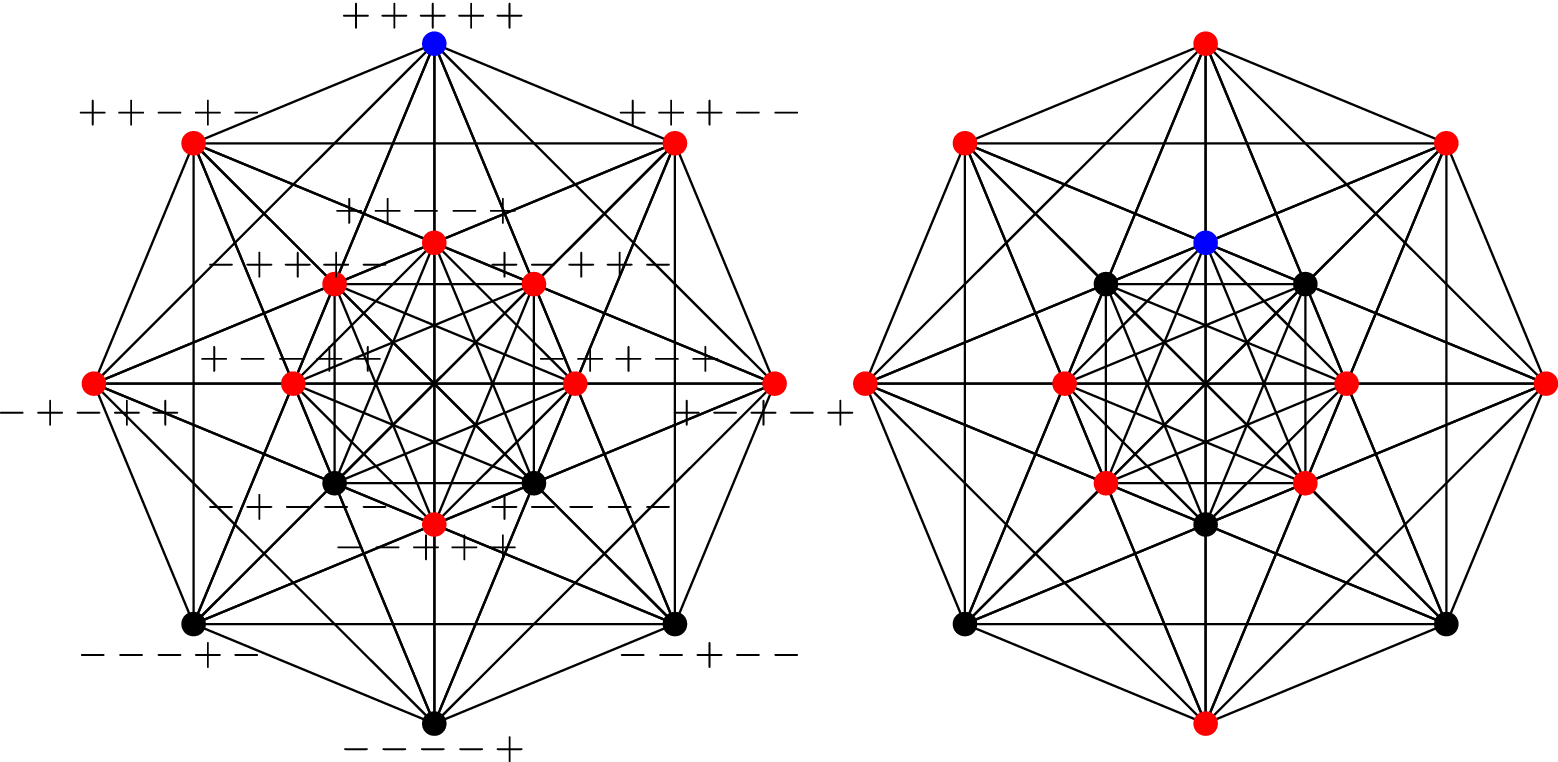
Figure 9 The orthogonal projection of the 1-skeleton of
![]() $1_{21}$
on the plane spanned by the vectors
$1_{21}$
on the plane spanned by the vectors
![]() $(\sqrt 2, \sqrt 2, 2-\sqrt 2, 2-\sqrt 2, 0)$
and
$(\sqrt 2, \sqrt 2, 2-\sqrt 2, 2-\sqrt 2, 0)$
and
![]() $(2-\sqrt 2, \sqrt 2-2, \sqrt 2, -\sqrt 2, 0)$
. The string
$(2-\sqrt 2, \sqrt 2-2, \sqrt 2, -\sqrt 2, 0)$
. The string
![]() $\pm \pm \pm \pm \pm $
indicates the projection of the vertex
$\pm \pm \pm \pm \pm $
indicates the projection of the vertex
![]() $(\pm 1, \pm 1, \pm 1, \pm 1, \pm 1)$
. Some edges are superposed along the projection, so two vertices that are connected by an edge on the plane projection may not be so in
$(\pm 1, \pm 1, \pm 1, \pm 1, \pm 1)$
. Some edges are superposed along the projection, so two vertices that are connected by an edge on the plane projection may not be so in
![]() $1_{21}$
. To clarify visually, for this ambiguity, we have chosen a blue vertex and painted in red the 10 vertices adjacent to it, in two cases (all the other cases are obtained by rotation).
$1_{21}$
. To clarify visually, for this ambiguity, we have chosen a blue vertex and painted in red the 10 vertices adjacent to it, in two cases (all the other cases are obtained by rotation).

Figure 10 The chosen colouring for
![]() $P^5$
.
$P^5$
.
The polytope
![]() $P^5$
has 10 ideal vertices. Each ideal vertex is dual to a 4-octahedral facet of
$P^5$
has 10 ideal vertices. Each ideal vertex is dual to a 4-octahedral facet of
![]() $1_{21}$
contained in a hyperplane
$1_{21}$
contained in a hyperplane
![]() $x_i = \pm 1$
. We deduce then that there are two types of 4-octahedral facets, depicted in Figure 11. Eight facets are of the left type, and two of the right type (all obtained by rotating the graphs shown in the figure). The vertices of the facets of the first type inherit an 8-colouring, while those of the facets of the second type inherit a 4-colouring.
$x_i = \pm 1$
. We deduce then that there are two types of 4-octahedral facets, depicted in Figure 11. Eight facets are of the left type, and two of the right type (all obtained by rotating the graphs shown in the figure). The vertices of the facets of the first type inherit an 8-colouring, while those of the facets of the second type inherit a 4-colouring.

Figure 11 The ten 4-octahedral facets of
![]() $1_{21}$
are of two types. Eight are obtained by rotating the type shown on the left, and two by rotating the type shown on the right. These are subgraphs of the 1-skeleton in Figure 10. Some edges are superposed.
$1_{21}$
are of two types. Eight are obtained by rotating the type shown on the left, and two by rotating the type shown on the right. These are subgraphs of the 1-skeleton in Figure 10. Some edges are superposed.
We have discovered that there are eight ideal vertices of the first type and two ideal vertices of the second type in
![]() $P^5$
. The link of an ideal vertex of the first type of
$P^5$
. The link of an ideal vertex of the first type of
![]() $P^5$
is an 8-coloured 4-cube C, while the link of an ideal vertex of the second type is a 4-coloured 4-cube C. Note that four and eight are precisely the minimum and maximum number of colours on a 4-cube. By Corollary 8, the counterimage of C consists of a single (since
$P^5$
is an 8-coloured 4-cube C, while the link of an ideal vertex of the second type is a 4-coloured 4-cube C. Note that four and eight are precisely the minimum and maximum number of colours on a 4-cube. By Corollary 8, the counterimage of C consists of a single (since
![]() $2^{8-8}=1$
) toric cusp section in the first case, and of
$2^{8-8}=1$
) toric cusp section in the first case, and of
![]() $2^{8-4} = 2^4 = 16$
toric cusp sections in the second case. Therefore, the hyperbolic manifold
$2^{8-4} = 2^4 = 16$
toric cusp sections in the second case. Therefore, the hyperbolic manifold
![]() $M^4$
has
$M^4$
has
![]() $8\cdot 1 + 2\cdot 16 = 40$
cusps overall. The first eight cusps lie above the eight vertices of the first type, and the remaining 32 cusps lie above the two vertices of the second type, distributed as 16 above each.
$8\cdot 1 + 2\cdot 16 = 40$
cusps overall. The first eight cusps lie above the eight vertices of the first type, and the remaining 32 cusps lie above the two vertices of the second type, distributed as 16 above each.
Using Sage, we have calculated the Betti numbers of
![]() $M^5$
:
$M^5$
:
We get of course,
![]() $\chi (M^5)=0$
.
$\chi (M^5)=0$
.
1.11 The manifold
 $M^6$
$M^6$
The hyperbolic polytope
![]() $P^6\subset {\mathbb {H}}^6$
is fully described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30], and we refer to these sources for more details. It has 27 facets, each isometric to
$P^6\subset {\mathbb {H}}^6$
is fully described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30], and we refer to these sources for more details. It has 27 facets, each isometric to
![]() $P^5$
. It also has 72 finite vertices and 27 ideal vertices. Every ideal vertex is opposed to a facet.
$P^5$
. It also has 72 finite vertices and 27 ideal vertices. Every ideal vertex is opposed to a facet.
The dual Gosset polytope
![]() $2_{21}$
has 27 vertices. We can represent them in the affine hyperspace of
$2_{21}$
has 27 vertices. We can represent them in the affine hyperspace of
![]() $ {\mathbb {R}}^7$
of equation
$ {\mathbb {R}}^7$
of equation
![]() $x_1 + \cdots + x_6 - 3x_7 = -1$
, as the vertices
$x_1 + \cdots + x_6 - 3x_7 = -1$
, as the vertices
and all the other vertices obtained from these by permuting the first six coordinates, so we get
![]() $6+15+6=27$
vertices in total (see [Reference Everitt, Ratcliffe and Tschantz14, Table 2]. Two vertices are connected by an edge if their Lorentzian product in
$6+15+6=27$
vertices in total (see [Reference Everitt, Ratcliffe and Tschantz14, Table 2]. Two vertices are connected by an edge if their Lorentzian product in
![]() $ {\mathbb {R}}^7$
with signature
$ {\mathbb {R}}^7$
with signature
![]() $(++++++-)$
is zero. The Gosset polytope
$(++++++-)$
is zero. The Gosset polytope
![]() $2_{21}$
has 99 facets; of these, 72 are regular 5-simplexes dual to the finite vertices of
$2_{21}$
has 99 facets; of these, 72 are regular 5-simplexes dual to the finite vertices of
![]() $P^6$
, and 27 are regular 5-octahedra dual to the ideal vertices of
$P^6$
, and 27 are regular 5-octahedra dual to the ideal vertices of
![]() $P^6$
.
$P^6$
.
Both
![]() $P^6$
and
$P^6$
and
![]() $2_{21}$
have many remarkable properties. To mention one, the 1-skeleton of
$2_{21}$
have many remarkable properties. To mention one, the 1-skeleton of
![]() $2_{21}$
is the configuration graph of the 27 lines in a general cubic surface (see [Reference Coxeter11]). A planar projection of the 1-skeleton of
$2_{21}$
is the configuration graph of the 27 lines in a general cubic surface (see [Reference Coxeter11]). A planar projection of the 1-skeleton of
![]() $2_{21}$
taken from [Reference Coxeter11] is shown in Figure 12. In the figure, we see that there are nine lines that intersect in the centre, containing each three mutually nonadjacent vertices. This suggests that the polytope may have a nice 9-colouring.
$2_{21}$
taken from [Reference Coxeter11] is shown in Figure 12. In the figure, we see that there are nine lines that intersect in the centre, containing each three mutually nonadjacent vertices. This suggests that the polytope may have a nice 9-colouring.

Figure 12 An orthogonal projection of the 1-skeleton of
![]() $2_{21}$
on the plane. Some edges are superposed. There are nine lines intersecting in the centre of the figure, each line containing three vertices that are mutually non incident.
$2_{21}$
on the plane. Some edges are superposed. There are nine lines intersecting in the centre of the figure, each line containing three vertices that are mutually non incident.
Inspired by the figure, we describe a 9-colouring for
![]() $2_{21}$
. The three vertices
$2_{21}$
. The three vertices
are mutually non connected by any edge since their Lorentzian products are not zero. We assign them the colour 1. If we permute cyclically the first six entries of these three vertices, we get five more triplets of mutually non connected vertices, and we assign them the colours
![]() $2,\ldots , 6$
. Finally, we assign the colours
$2,\ldots , 6$
. Finally, we assign the colours
![]() $7,8,9$
to the following remaining triplets of mutually disjoint vertices:
$7,8,9$
to the following remaining triplets of mutually disjoint vertices:
 $$ \begin{gather*} (1,0,1,0,0,0,1), \quad (0,1,0,0,1,0,1), \quad (0,0,0,1,0,1,1); \\ (0,1,0,1,0,0,1), \quad (0,0,1,0,0,1,1), \quad (1,0,0,0,1,0,1); \\ (0,0,1,0,1,0,1), \quad (1,0,0,1,0,0,1), \quad (0,1,0,0,0,1,1). \end{gather*} $$
$$ \begin{gather*} (1,0,1,0,0,0,1), \quad (0,1,0,0,1,0,1), \quad (0,0,0,1,0,1,1); \\ (0,1,0,1,0,0,1), \quad (0,0,1,0,0,1,1), \quad (1,0,0,0,1,0,1); \\ (0,0,1,0,1,0,1), \quad (1,0,0,1,0,0,1), \quad (0,1,0,0,0,1,1). \end{gather*} $$
We equip
![]() $P^6$
with this 9-colouring. Each triple of facets with the same colour is called a triplet. The colouring produces a hyperbolic 6-manifold
$P^6$
with this 9-colouring. Each triple of facets with the same colour is called a triplet. The colouring produces a hyperbolic 6-manifold
![]() $M^6$
, tessellated into
$M^6$
, tessellated into
![]() $2^9 = 512$
copies of
$2^9 = 512$
copies of
![]() $P^6$
. We have
$P^6$
. We have
![]() $\chi (M^6) = -512/8 = -64$
.
$\chi (M^6) = -512/8 = -64$
.
The polytope
![]() $P^6$
has 27 ideal vertices. Using our program in Sage [Reference Martelli39], we discover that the link of each of the 27 ideal vertices of
$P^6$
has 27 ideal vertices. Using our program in Sage [Reference Martelli39], we discover that the link of each of the 27 ideal vertices of
![]() $P^6$
is a 9-coloured 5-cube C. We show one explicit example. Every facet F of
$P^6$
is a 9-coloured 5-cube C. We show one explicit example. Every facet F of
![]() $P^6$
is opposite to an ideal vertex, which is incident precisely to those facets that are not incident to F. Correspondingly, every vertex v in
$P^6$
is opposite to an ideal vertex, which is incident precisely to those facets that are not incident to F. Correspondingly, every vertex v in
![]() $2_{21}$
is opposite to a 5-octahedral facet, whose vertices are precisely those that are not connected to v. The 5-octahedral facet opposite to the vertex
$2_{21}$
is opposite to a 5-octahedral facet, whose vertices are precisely those that are not connected to v. The 5-octahedral facet opposite to the vertex
![]() $v=(-1,0,0,0,0,0,0)$
has the following vertices:
$v=(-1,0,0,0,0,0,0)$
has the following vertices:
 $$ \begin{gather*} (1,1,0,0,0,0,1),\! (1,0,1,0,0,0,1),\! (1,0,0,1,0,0,1),\! (1,0,0,0,1,0,1),\! (1,0,0,0,0,1,1), \\ (1,0,1,1,1,1,2),\! (1,1,0,1,1,1,2),\! (1,1,1,0,1,1,2),\! (1,1,1,1,0,1,2),\! (1,1,1,1,1,0,2). \end{gather*} $$
$$ \begin{gather*} (1,1,0,0,0,0,1),\! (1,0,1,0,0,0,1),\! (1,0,0,1,0,0,1),\! (1,0,0,0,1,0,1),\! (1,0,0,0,0,1,1), \\ (1,0,1,1,1,1,2),\! (1,1,0,1,1,1,2),\! (1,1,1,0,1,1,2),\! (1,1,1,1,0,1,2),\! (1,1,1,1,1,0,2). \end{gather*} $$
The two vertices that lie in the same column are not connected. Their colours are
 $$ \begin{gather*} 1,\ 7,\ 9,\ 8,\ 6, \\ 1,\ 2,\ 3,\ 4,\ 5. \end{gather*} $$
$$ \begin{gather*} 1,\ 7,\ 9,\ 8,\ 6, \\ 1,\ 2,\ 3,\ 4,\ 5. \end{gather*} $$
All the nine colours are present. As we said above, using our Sage program, we discover that a similar configuration holds at every vertex v. Therefore, by Corollary 8, the counterimage of C consists of a single (since
![]() $2^{9-9}=1$
) toric cusp section. We deduce finally that the hyperbolic manifold
$2^{9-9}=1$
) toric cusp section. We deduce finally that the hyperbolic manifold
![]() $M^6$
has 27 cusps, one above each vertex of
$M^6$
has 27 cusps, one above each vertex of
![]() $P^6$
. The Betti numbers of
$P^6$
. The Betti numbers of
![]() $M^6$
, calculated by our program, are:
$M^6$
, calculated by our program, are:
We get
![]() $\chi (M^6)=-64$
again.
$\chi (M^6)=-64$
again.
1.12 The manifold
 $M^7$
$M^7$
The hyperbolic polytope
![]() $P^7 \subset {\mathbb {H}}^7$
is described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30]. It has 56 facets, each isometric to
$P^7 \subset {\mathbb {H}}^7$
is described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30]. It has 56 facets, each isometric to
![]() $P^6$
. It also has 576 finite vertices and 126 ideal vertices.
$P^6$
. It also has 576 finite vertices and 126 ideal vertices.
The dual Gosset polytope
![]() $3_{21}$
has 56 vertices. We will discover below that the 56 vertices can be partitioned into 14 sets of four mutually disjoint vertices, called quartets. This partition will be induced from a colouring of
$3_{21}$
has 56 vertices. We will discover below that the 56 vertices can be partitioned into 14 sets of four mutually disjoint vertices, called quartets. This partition will be induced from a colouring of
![]() $P^8$
, that is in turn easily described using octonions. The precise description of the partition is given below in Section 1.14.
$P^8$
, that is in turn easily described using octonions. The precise description of the partition is given below in Section 1.14.
We equip
![]() $P^7$
with the 14-colouring induced by the partition into 14 quartets. This produces a hyperbolic 7-manifold
$P^7$
with the 14-colouring induced by the partition into 14 quartets. This produces a hyperbolic 7-manifold
![]() $M^7$
, tessellated into
$M^7$
, tessellated into
![]() $2^{14}=16,384$
copies of
$2^{14}=16,384$
copies of
![]() $P^7$
.
$P^7$
.
The polytope
![]() $P^7$
has 126 ideal vertices. Using our Sage program, we discover that, similarly as with
$P^7$
has 126 ideal vertices. Using our Sage program, we discover that, similarly as with
![]() $P^5$
, there are two types of ideal vertices with respect to the chosen 14-colouring of
$P^5$
, there are two types of ideal vertices with respect to the chosen 14-colouring of
![]() $P^7$
. The first type consists of 112 vertices, and the second type only 14. The link of an ideal vertex of the first type is a 12-coloured 6-cube C, while the link of an ideal vertex of the second type is a 6-coloured 6-cube. Note that, as with
$P^7$
. The first type consists of 112 vertices, and the second type only 14. The link of an ideal vertex of the first type is a 12-coloured 6-cube C, while the link of an ideal vertex of the second type is a 6-coloured 6-cube. Note that, as with
![]() $P_5$
, the numbers 6 and 12 are the minimum and maximum number of colours in a 6-cube. From Corollary 8, we deduce that
$P_5$
, the numbers 6 and 12 are the minimum and maximum number of colours in a 6-cube. From Corollary 8, we deduce that
![]() $M^7$
has
$M^7$
has
![]() $14 \cdot 2^{14-6} + 112 \cdot 2^{14-12} = 4,032$
cusps overall.
$14 \cdot 2^{14-6} + 112 \cdot 2^{14-12} = 4,032$
cusps overall.
Using Sage, we have calculated the Betti numbers of
![]() $M^7$
:
$M^7$
:
We get of course,
![]() $\chi (M^7)=0$
.
$\chi (M^7)=0$
.
1.13 The manifold
 $M^8$
$M^8$
The hyperbolic polytope
![]() $P^8\subset {\mathbb {H}}^8$
is described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30]. It has 240 facets, each isometric to
$P^8\subset {\mathbb {H}}^8$
is described in [Reference Everitt, Ratcliffe and Tschantz14, Reference Potyagailo and Vinberg30]. It has 240 facets, each isometric to
![]() $P^7$
. It also has 17,280 finite vertices and 2,160 ideal vertices.
$P^7$
. It also has 17,280 finite vertices and 2,160 ideal vertices.
The dual Gosset polytope
![]() $4_{21}$
has 240 vertices. This beautiful albeit complicated polytope can be described elegantly using octonions, much in the same way as the 4-dimensional 24-cell may be defined using quaternions. This viewpoint is crucial in this paper, so we introduce it carefully.
$4_{21}$
has 240 vertices. This beautiful albeit complicated polytope can be described elegantly using octonions, much in the same way as the 4-dimensional 24-cell may be defined using quaternions. This viewpoint is crucial in this paper, so we introduce it carefully.
A 3-colouring for the 24-cell
To warm up, we start by recalling that the 24 vertices of the 24-cell are the quaternions
Two such vertices are adjacent along an edge if and only if their Euclidean scalar product is
![]() $\frac 12$
(we identify the quaternions space with the Euclidean
$\frac 12$
(we identify the quaternions space with the Euclidean
![]() $ {\mathbb {R}}^4$
, as usual). Every vertex is adjacent to eight other vertices.
$ {\mathbb {R}}^4$
, as usual). Every vertex is adjacent to eight other vertices.
We can assign three colours to the 24 vertices, by subdividing them into three sets of eight vertices each, that we call octets. These are:
-
(1)
 $ \pm 1, \pm i, \pm j, \pm k$
;
$ \pm 1, \pm i, \pm j, \pm k$
; -
(2) the elements
 $\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an even number of minus signs;
$\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an even number of minus signs; -
(3) the elements
 $\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an odd number of minus signs.
$\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an odd number of minus signs.
The scalar product of two vertices lying in the same octet is an integer, so it is never
![]() $\frac 12$
. Therefore, this indeed defines a 3-colouring of the vertices of the 24-cell. Since the dual of a 24-cell is another 24-cell, we also get a 3-colouring of the facets of the dual 24-cell. This colouring was heavily employed in [Reference Kolpakov and Martelli26].
$\frac 12$
. Therefore, this indeed defines a 3-colouring of the vertices of the 24-cell. Since the dual of a 24-cell is another 24-cell, we also get a 3-colouring of the facets of the dual 24-cell. This colouring was heavily employed in [Reference Kolpakov and Martelli26].
Here is an algebraic description of this 3-colouring that will be useful below. The 24 vertices of the 24-cell described above form a group called the binary tetrahedral group. The eight elements
![]() $ \pm 1, \pm i, \pm j, \pm k$
form a normal subgroup of index 3, called the quaternion group and indicated with the symbol
$ \pm 1, \pm i, \pm j, \pm k$
form a normal subgroup of index 3, called the quaternion group and indicated with the symbol
![]() $Q_8$
. The octets are just the three lateral classes of
$Q_8$
. The octets are just the three lateral classes of
![]() $Q_8$
.
$Q_8$
.
Octonions
We now turn to the Gosset polytope
![]() $4_{21}$
and the octonions. For a nice introduction to the subject, we recommend [Reference Baez5]. We describe an octonion as a linear combination of
$4_{21}$
and the octonions. For a nice introduction to the subject, we recommend [Reference Baez5]. We describe an octonion as a linear combination of
![]() $1, e_1, e_2, \ldots , e_7$
. We have
$1, e_1, e_2, \ldots , e_7$
. We have
![]() $e_i^2 = -1$
, and the multiplication of two distinct elements,
$e_i^2 = -1$
, and the multiplication of two distinct elements,
![]() $e_i$
and
$e_i$
and
![]() $e_j$
, is beautifully described by the Fano plane shown in Figure 13. The Fano plane is the projective plane over
$e_j$
, is beautifully described by the Fano plane shown in Figure 13. The Fano plane is the projective plane over
![]() ${\mathbb {Z}}_2$
, and it contains seven points and seven oriented lines: every line is a cyclically ordered triple of points as in the figure. For every
${\mathbb {Z}}_2$
, and it contains seven points and seven oriented lines: every line is a cyclically ordered triple of points as in the figure. For every
![]() $i\neq j$
, we have
$i\neq j$
, we have
![]() $e_ie_j = \pm e_k$
, where
$e_ie_j = \pm e_k$
, where
![]() $e_k$
is the third vertex in the unique line containing
$e_k$
is the third vertex in the unique line containing
![]() $e_i$
and
$e_i$
and
![]() $e_j$
, and the sign is positive if and only if the line is cyclically oriented like
$e_j$
, and the sign is positive if and only if the line is cyclically oriented like
![]() $e_i\to e_j \to e_k$
. So, for instance,
$e_i\to e_j \to e_k$
. So, for instance,
![]() $e_1e_2 = e_4$
and
$e_1e_2 = e_4$
and
![]() $e_1e_6 = -e_5$
. In general, we get
$e_1e_6 = -e_5$
. In general, we get
where the subscripts run modulo 7. The product is neither commutative nor associative: for every
![]() $i,j,k$
, we have
$i,j,k$
, we have
where the sign is
![]() $+1$
if and only if
$+1$
if and only if
![]() $e_i,e_j,e_k$
belong to the same line in the Fano plane (which is always the case, if
$e_i,e_j,e_k$
belong to the same line in the Fano plane (which is always the case, if
![]() $i,j,k$
are not distinct).
$i,j,k$
are not distinct).

Figure 13 The Fano plane. The circle should be interpreted as a line.
A 15-colouring for the Gosset polytope
 $4_{21}$
$4_{21}$
The 240 vertices of the Gosset polytope
![]() $4_{21}$
are the octonions
$4_{21}$
are the octonions
 $$ \begin{gather*} \pm 1,\ \pm e_1,\ \pm e_2, \ \pm e_3, \ \pm e_4, \ \pm e_5, \ \pm e_6, \ \pm e_7, \\ \tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3}), \quad \tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6}), \end{gather*} $$
$$ \begin{gather*} \pm 1,\ \pm e_1,\ \pm e_2, \ \pm e_3, \ \pm e_4, \ \pm e_5, \ \pm e_6, \ \pm e_7, \\ \tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3}), \quad \tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6}), \end{gather*} $$
where n runs modulo 7. Although we will not need this information, we mention that these are (up to rescaling) precisely the 240 nontrivial elements of smallest norm in the
![]() $E_8$
lattice.
$E_8$
lattice.
We have 16 elements of type
![]() $\pm 1$
or
$\pm 1$
or
![]() $\pm e_i$
. Each line l in the Fano plane contains three vertices
$\pm e_i$
. Each line l in the Fano plane contains three vertices
![]() $e_n, e_{n+1}, e_{n+3}$
and determines 16 elements of type
$e_n, e_{n+1}, e_{n+3}$
and determines 16 elements of type
![]() $\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and 16 elements of type
$\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and 16 elements of type
![]() $\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
, so we indeed get
$\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
, so we indeed get
![]() $16 + 7 \cdot 16 + 7 \cdot 16 = 15 \cdot 16 = 240$
vertices overall. Two vertices of
$16 + 7 \cdot 16 + 7 \cdot 16 = 15 \cdot 16 = 240$
vertices overall. Two vertices of
![]() $4_{21}$
are connected by an edge if and only if their Euclidean scalar product is
$4_{21}$
are connected by an edge if and only if their Euclidean scalar product is
![]() $\frac 12$
. One can check that every vertex is adjacent to 56 other vertices (its link is dual to
$\frac 12$
. One can check that every vertex is adjacent to 56 other vertices (its link is dual to
![]() $P^7$
that has 56 facets).
$P^7$
that has 56 facets).
Similarly to what we did with the 24-cell, we can assign a 15-colouring to
![]() $4_{21}$
by subdividing the 240 vertices into 15 sets of 16 elements each; we call each such set a hextet. The hextets are:
$4_{21}$
by subdividing the 240 vertices into 15 sets of 16 elements each; we call each such set a hextet. The hextets are:
-
(1)
 $\pm 1,\pm e_1, \pm e_2, \pm e_3, \pm e_4, \pm e_5, \pm e_6, \pm e_7$
;
$\pm 1,\pm e_1, \pm e_2, \pm e_3, \pm e_4, \pm e_5, \pm e_6, \pm e_7$
; -
(2) the elements
 $\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
$\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
 $\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an even number of minus signs;
$\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an even number of minus signs; -
(3) the elements
 $\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
$\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
 $\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an odd number of minus signs.
$\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an odd number of minus signs.
The hextets of type (2) and (3) depend on the choice of n modulo 7. So we get
![]() $1+2\cdot 7 = 15$
hextets overall. One can check that the scalar product of two vertices lying in the same hextet is always an integer, so it is never
$1+2\cdot 7 = 15$
hextets overall. One can check that the scalar product of two vertices lying in the same hextet is always an integer, so it is never
![]() $\frac 12$
. Therefore, we can assign the same colour to all the 16 members of a given hextet, and, hence, obtain a 15-colouring for
$\frac 12$
. Therefore, we can assign the same colour to all the 16 members of a given hextet, and, hence, obtain a 15-colouring for
![]() $4_{21}$
as promised.
$4_{21}$
as promised.
Algebraic description
There is an algebraic interpretation for the 15-colouring of
![]() $4_{21}$
analogous to that for the 3-colouring of the 24-cell. We warn the reader that some caution is needed when passing from quaternions to octonions: first, the product of octonions is notoriously nonassociative; second, contrary to a common mistake (see [Reference Conway and Smith10, Chapter 9] for a discussion), and as proved by Coxeter [Reference Coxeter12], the 240 vertices of
$4_{21}$
analogous to that for the 3-colouring of the 24-cell. We warn the reader that some caution is needed when passing from quaternions to octonions: first, the product of octonions is notoriously nonassociative; second, contrary to a common mistake (see [Reference Conway and Smith10, Chapter 9] for a discussion), and as proved by Coxeter [Reference Coxeter12], the 240 vertices of
![]() $4_{21}$
are not closed under multiplication! Indeed, the product of the two vertices
$4_{21}$
are not closed under multiplication! Indeed, the product of the two vertices
is not a vertex. We could fix this via a single reflection that transforms the 240 vertices into a multiplicatively closed set (this is explained in [Reference Conway and Smith10, Section 9.2]), thus obtaining another isometric description of
![]() $4_{21}$
, but we do not really need this here, so we just keep them as they are. The only thing that we need here is that the 240 octonions are closed under left multiplication by each of the 16 elements in the hextet
$4_{21}$
, but we do not really need this here, so we just keep them as they are. The only thing that we need here is that the 240 octonions are closed under left multiplication by each of the 16 elements in the hextet
![]() $S=\{\pm 1, \pm e_i\}$
, a fact that can be verified easily. The set S is closed under multiplication, but it is not a group since it is not associative. One can also verify that the left multiplication by each element of S preserves each hextet, and that this ‘action’ of S is free and transitive, in the sense that for very pair of distinct elements in a hextet, there is a unique element of S that sends the first to the second by left-multiplication.
$S=\{\pm 1, \pm e_i\}$
, a fact that can be verified easily. The set S is closed under multiplication, but it is not a group since it is not associative. One can also verify that the left multiplication by each element of S preserves each hextet, and that this ‘action’ of S is free and transitive, in the sense that for very pair of distinct elements in a hextet, there is a unique element of S that sends the first to the second by left-multiplication.
Summing up, the 15 hextets that we have constructed are the orbits of the action of S by left-multiplication on the set of 240 vertices of
![]() $4_{21}$
. This is analogous to the 3-colouring of the 24-cell, where the three octets are the orbits of the action of the quaternion group
$4_{21}$
. This is analogous to the 3-colouring of the 24-cell, where the three octets are the orbits of the action of the quaternion group
![]() $Q_8$
by left multiplication.
$Q_8$
by left multiplication.
The manifold
 $M^8$
$M^8$
We equip
![]() $P^8$
with the 15-colouring just defined. This produces a hyperbolic 8-manifold
$P^8$
with the 15-colouring just defined. This produces a hyperbolic 8-manifold
![]() $M^8$
, tessellated into
$M^8$
, tessellated into
![]() $2^{15} = 32,768$
copies of
$2^{15} = 32,768$
copies of
![]() $P^8$
. We have
$P^8$
. We have
![]() $\chi (M^8) = 2^{15}\cdot 17/2 = 27,8528$
.
$\chi (M^8) = 2^{15}\cdot 17/2 = 27,8528$
.
The polytope
![]() $P^8$
has 2,160 ideal vertices. Using our Sage program, we discover a phenomenon that was already present with
$P^8$
has 2,160 ideal vertices. Using our Sage program, we discover a phenomenon that was already present with
![]() $P^5$
and
$P^5$
and
![]() $P^7$
. The ideal vertices are of two types: the first type contains 1,920 of them, and the second type 240. The link of a vertex of the first type is a 14-coloured 7-cube, while the link of a vertex of the second type is a 7-coloured 7-cube. As with
$P^7$
. The ideal vertices are of two types: the first type contains 1,920 of them, and the second type 240. The link of a vertex of the first type is a 14-coloured 7-cube, while the link of a vertex of the second type is a 7-coloured 7-cube. As with
![]() $P^5$
and
$P^5$
and
![]() $P^7$
, we note that 7 and 14 are the minimum and maximum possible number of colours in a 7-cube. From Corollary 8, we deduce that
$P^7$
, we note that 7 and 14 are the minimum and maximum possible number of colours in a 7-cube. From Corollary 8, we deduce that
![]() $M^8$
has
$M^8$
has
![]() $240\cdot 2^{15-7} + 1,920 \cdot 2^{15-14} = 65,280$
cusps.
$240\cdot 2^{15-7} + 1,920 \cdot 2^{15-14} = 65,280$
cusps.
Using Sage, we have calculated the Betti numbers of
![]() $M^8$
:
$M^8$
:
 $$ \begin{gather*} b_0 = 1,\quad b_1 = 365, \quad b_2 = 33,670, \quad b_3 = 583,290, \\ b_4 = 1,783,226, \quad b_5 = 1,346,030, \quad b_6 = 456,595, \quad b_7 = 65,279. \end{gather*} $$
$$ \begin{gather*} b_0 = 1,\quad b_1 = 365, \quad b_2 = 33,670, \quad b_3 = 583,290, \\ b_4 = 1,783,226, \quad b_5 = 1,346,030, \quad b_6 = 456,595, \quad b_7 = 65,279. \end{gather*} $$
We get
![]() $\chi (M^8)=278,528$
again.
$\chi (M^8)=278,528$
again.
1.14 Back to the polytope
 $P^7$
$P^7$
The polytope
![]() $P^7$
is a facet of
$P^7$
is a facet of
![]() $P^8$
. We think of
$P^8$
. We think of
![]() $P^7$
as the facet dual to the vertex 1 of
$P^7$
as the facet dual to the vertex 1 of
![]() $4_{21}$
. As we already said, we equip
$4_{21}$
. As we already said, we equip
![]() $P^7$
with the colouring induced by the 15-colouring of
$P^7$
with the colouring induced by the 15-colouring of
![]() $P^8$
just introduced.
$P^8$
just introduced.
We study this inherited colouring of
![]() $P^7$
. We think of
$P^7$
. We think of
![]() $3_{21}$
as the link figure of the vertex
$3_{21}$
as the link figure of the vertex
![]() $1$
of
$1$
of
![]() $4_{21}$
. The vertices of
$4_{21}$
. The vertices of
![]() $4_{21}$
adjacent to
$4_{21}$
adjacent to
![]() $1$
are precisely those of the form
$1$
are precisely those of the form
where n runs modulo 7. So we get
![]() $7\cdot 8 = 56$
vertices, as required. These vertices are contained in the hyperplane
$7\cdot 8 = 56$
vertices, as required. These vertices are contained in the hyperplane
![]() $x_0 = \frac 12$
, and their convex hull is
$x_0 = \frac 12$
, and their convex hull is
![]() $3_{21}$
. Two such vertices are connected by an edge in
$3_{21}$
. Two such vertices are connected by an edge in
![]() $3_{21}$
if and only if their scalar product is
$3_{21}$
if and only if their scalar product is
![]() $\frac 12$
.
$\frac 12$
.
The 15-colouring of
![]() $4_{21}$
induces a 14-colouring of
$4_{21}$
induces a 14-colouring of
![]() $3_{21}$
that partitions the 56 vertices into 14 sets of four vertices each, that we call quartets. Each quartet consists of the vertices
$3_{21}$
that partitions the 56 vertices into 14 sets of four vertices each, that we call quartets. Each quartet consists of the vertices
![]() $\frac 12(1 \pm e_n \pm e_{n+1} \pm e_{n+3})$
that share the same n and the same parity of the minus signs.
$\frac 12(1 \pm e_n \pm e_{n+1} \pm e_{n+3})$
that share the same n and the same parity of the minus signs.
1.15 Volumes
We have constructed a colouring on each polytope
![]() $P^3, \ldots , P^8$
, and, hence, obtained a list of manifolds
$P^3, \ldots , P^8$
, and, hence, obtained a list of manifolds
![]() $M^3,\ldots , M^8$
. Table 3 summarises the colouring type of each polytope.
$M^3,\ldots , M^8$
. Table 3 summarises the colouring type of each polytope.
Table 3 The colouring type of each
![]() $P^3,\ldots , P^8$
.
$P^3,\ldots , P^8$
.

The volumes of the hyperbolic manifolds
![]() $M^3, \ldots , M^8$
are listed in Table 4. In even dimension
$M^3, \ldots , M^8$
are listed in Table 4. In even dimension
![]() $n=2m$
, we have used the Gauss-Bonnet formula
$n=2m$
, we have used the Gauss-Bonnet formula
In odd dimension, we have
The symbols
![]() $\zeta $
and L indicate the Riemann and Dirichlet functions (see [Reference Everitt, Ratcliffe and Tschantz14, Reference Ratcliffe and Tschantz31]).
$\zeta $
and L indicate the Riemann and Dirichlet functions (see [Reference Everitt, Ratcliffe and Tschantz14, Reference Ratcliffe and Tschantz31]).
Table 4 The volume, the Euler characteristic and the number of cusps of each hyperbolic n-manifold
![]() $M^n$
.
$M^n$
.

1.16 The chosen colourings are all minimal
Although we will not need it, we mention the following fact.
Proposition 10. The colourings for
![]() $P^3,\ldots , P^8$
defined in the previous sections have the smallest possible number of colours for each polytope.
$P^3,\ldots , P^8$
defined in the previous sections have the smallest possible number of colours for each polytope.
Proof. We can verify by hand when
![]() $n\leq 5$
and, using our Sage program, when
$n\leq 5$
and, using our Sage program, when
![]() $6\leq n \leq 8$
that the maximum number of pairwise disjoint facets in
$6\leq n \leq 8$
that the maximum number of pairwise disjoint facets in
![]() $P^n$
is equal to 2, 2, 2, 3, 4, 16 when
$P^n$
is equal to 2, 2, 2, 3, 4, 16 when
![]() $n=3,4,5,6,7,8$
. These are precisely the cardinalities of the facets sharing the same colour for all n (see Table 3). Therefore, we cannot find a more efficient colouring than the one listed in the table.
$n=3,4,5,6,7,8$
. These are precisely the cardinalities of the facets sharing the same colour for all n (see Table 3). Therefore, we cannot find a more efficient colouring than the one listed in the table.
1.17 The last nonzero Betti number
The Betti numbers
![]() $b_i$
and the number c of cusps of each
$b_i$
and the number c of cusps of each
![]() $M^n$
were listed in Table 1. In all the cases, we have
$M^n$
were listed in Table 1. In all the cases, we have
![]() $b_{n-1} = c-1$
. Since
$b_{n-1} = c-1$
. Since
![]() $M^n$
is the interior of a compact manifold with c boundary components, in general, we must have
$M^n$
is the interior of a compact manifold with c boundary components, in general, we must have
![]() $b_{n-1} \geq c-1$
. Therefore, here, the Betti number
$b_{n-1} \geq c-1$
. Therefore, here, the Betti number
![]() $b_{n-1}$
is as small as possible, given the number c of cusps.
$b_{n-1}$
is as small as possible, given the number c of cusps.
2 The algebraic fibrations
We have constructed some hyperbolic manifolds
![]() $M^3,\ldots , M^8$
, and our aim is now to build some nice maps
$M^3,\ldots , M^8$
, and our aim is now to build some nice maps
![]() $f\colon M^n \to S^1$
for all
$f\colon M^n \to S^1$
for all
![]() $n=3,\ldots , 8$
. We produce these maps by assigning to each
$n=3,\ldots , 8$
. We produce these maps by assigning to each
![]() $P^n$
an appropriate state (as prescribed by [Reference Jankiewicz, Norin and Wise18]). We then study the maps by applying some fundamental results of [Reference Bestvina and Brady7].
$P^n$
an appropriate state (as prescribed by [Reference Jankiewicz, Norin and Wise18]). We then study the maps by applying some fundamental results of [Reference Bestvina and Brady7].
2.1 States
Let
![]() $P \subset {\mathbb {X}}^n$
be a right-angled polytope in some space
$P \subset {\mathbb {X}}^n$
be a right-angled polytope in some space
![]() $ {\mathbb {X}}^n = {\mathbb {H}}^n, {\mathbb {R}}^n$
or
$ {\mathbb {X}}^n = {\mathbb {H}}^n, {\mathbb {R}}^n$
or
![]() $S^n$
. Following [Reference Jankiewicz, Norin and Wise18], a state is a partition of the facets of P into two subsets, that we denote as I (in) and O (out). Every facet thus inherits a status I or O.
$S^n$
. Following [Reference Jankiewicz, Norin and Wise18], a state is a partition of the facets of P into two subsets, that we denote as I (in) and O (out). Every facet thus inherits a status I or O.
Let P be equipped with a colouring with c colours. This induces a free action of
![]() ${\mathbb {Z}}_2^c$
on the set of all the states of P, in the following way. For every
${\mathbb {Z}}_2^c$
on the set of all the states of P, in the following way. For every
![]() $j\in \{1,\ldots , c\}$
, the basis element
$j\in \{1,\ldots , c\}$
, the basis element
![]() $e_j$
acts by reversing the I/O status of every facet of P coloured by j, while leaving the status of the other facets unaffected. The action is free, hence, each orbit consists of
$e_j$
acts by reversing the I/O status of every facet of P coloured by j, while leaving the status of the other facets unaffected. The action is free, hence, each orbit consists of
![]() $2^c$
distinct states.
$2^c$
distinct states.
2.2 Diagonal maps
As discovered in [Reference Jankiewicz, Norin and Wise18], the choice of a colouring and a state for a right-angled polytope P induce both a manifold M and a diagonal map
![]() $M \to S^1$
. (The construction of [Reference Jankiewicz, Norin and Wise18] is actually more general than this, but this interpretation is enough here.) Shortly:
$M \to S^1$
. (The construction of [Reference Jankiewicz, Norin and Wise18] is actually more general than this, but this interpretation is enough here.) Shortly:

We explain how this works. We already know how a colouring on P produces a manifold M, so it remains to explain how a state induces a map
![]() $f\colon M\to S^1$
.
$f\colon M\to S^1$
.
The manifold M is tessellated into the
![]() $2^c$
polytopes
$2^c$
polytopes
![]() $P_v$
with varying
$P_v$
with varying
![]() $v\in {\mathbb {Z}}_2^c$
. Since these are right-angled, the tessellation is dual to a cube complex C with
$v\in {\mathbb {Z}}_2^c$
. Since these are right-angled, the tessellation is dual to a cube complex C with
![]() $2^c$
vertices. We work in the piecewise-linear category (see [Reference Rourke and Sanderson34] for an introduction) and think of C as piecewise-linearly embedded inside M. If P has some ideal vertices (as it will be the case with all the polytopes
$2^c$
vertices. We work in the piecewise-linear category (see [Reference Rourke and Sanderson34] for an introduction) and think of C as piecewise-linearly embedded inside M. If P has some ideal vertices (as it will be the case with all the polytopes
![]() $P^n\subset {\mathbb {H}}^n$
that we consider here), the complement
$P^n\subset {\mathbb {H}}^n$
that we consider here), the complement
![]() $M \setminus C$
consists of open cusps, so there is a deformation retraction
$M \setminus C$
consists of open cusps, so there is a deformation retraction
![]() $r\colon M \to C$
. The cube complex C is a spine of M.
$r\colon M \to C$
. The cube complex C is a spine of M.
We indicate the vertex of C dual to
![]() $P_v$
simply as v, so the vertices of C are identified with
$P_v$
simply as v, so the vertices of C are identified with
![]() ${\mathbb {Z}}_2^c$
. Here, v stands both for a vector of
${\mathbb {Z}}_2^c$
. Here, v stands both for a vector of
![]() ${\mathbb {Z}}_2^c$
and a vertex of C.
${\mathbb {Z}}_2^c$
and a vertex of C.
The edges of C are dual to the facets of the tessellation: an edge of C connects v and
![]() $v+e_j$
if the dual facet F is coloured as j. So, in particular, there are k distinct edges connecting v to
$v+e_j$
if the dual facet F is coloured as j. So, in particular, there are k distinct edges connecting v to
![]() $v+e_j$
, where k is the number of facets in P coloured with j. In all the colourings that we have chosen for the polytopes
$v+e_j$
, where k is the number of facets in P coloured with j. In all the colourings that we have chosen for the polytopes
![]() $P^n$
, the number k does not depend on the colour j. The 1-skeleton of C for
$P^n$
, the number k does not depend on the colour j. The 1-skeleton of C for
![]() $P=P^3$
is shown in Figure 14.
$P=P^3$
is shown in Figure 14.
Figure 14 The 1-skeleton of the dual cubulation C for
![]() $M^3$
, tessellated into eight polyhedra
$M^3$
, tessellated into eight polyhedra
![]() $P_v^3$
. The polyhedron
$P_v^3$
. The polyhedron
![]() $P^3$
is 3-coloured, and each colour is painted on two faces. The vertices of C are identified with
$P^3$
is 3-coloured, and each colour is painted on two faces. The vertices of C are identified with
![]() ${\mathbb {Z}}_2^3$
. There are two edges connecting v and
${\mathbb {Z}}_2^3$
. There are two edges connecting v and
![]() $v+e_j$
corresponding to the two faces in
$v+e_j$
corresponding to the two faces in
![]() $P_v$
with the same colour j, for each
$P_v$
with the same colour j, for each
![]() $j=1,2,3$
.
$j=1,2,3$
.
Example 11. If we consider
![]() $P = P^8$
with its 15-colouring, there are
$P = P^8$
with its 15-colouring, there are
![]() $2^{15}$
vertices in C, and 16 edges connecting v to
$2^{15}$
vertices in C, and 16 edges connecting v to
![]() $v+e_j$
for every v and every j.
$v+e_j$
for every v and every j.
Let now s be a fixed state for P. The state s induces an orientation on all the edges of C, in the simplest possible way: consider an edge connecting v and
![]() $v+e_j$
, where the j-th component of v is zero, that is
$v+e_j$
, where the j-th component of v is zero, that is
![]() $v_j=0$
. The edge is dual to some facet of the tessellation that is a precise identical copy of a facet F of P. If the status of F is O, we orient the edge outward, that is from v to
$v_j=0$
. The edge is dual to some facet of the tessellation that is a precise identical copy of a facet F of P. If the status of F is O, we orient the edge outward, that is from v to
![]() $v+e_j$
, while if it is I, we orient it inward, from
$v+e_j$
, while if it is I, we orient it inward, from
![]() $v+e_j$
to v.
$v+e_j$
to v.
By construction, this orientation is coherent, that is on every square of C (and, hence, on any k-cube), the orientations of two opposite edges match as in Figure 15. This crucial fact allows us to apply the Bestvina-Brady theory [Reference Bestvina and Brady7]. We identify every k-cube of C with the standard k-cube
![]() $[0,1]^k \subset {\mathbb {R}}^k$
, so that the orientations on the edges of C match with the orientations of the axis in
$[0,1]^k \subset {\mathbb {R}}^k$
, so that the orientations on the edges of C match with the orientations of the axis in
![]() $ {\mathbb {R}}^k$
. The diagonal map on the standard k-cube is
$ {\mathbb {R}}^k$
. The diagonal map on the standard k-cube is
The diagonal maps on the k-cubes of C match to give a well-defined continuous piecewise-linear map
![]() $C \to S^1$
. By precomposing it with the deformation retraction
$C \to S^1$
. By precomposing it with the deformation retraction
![]() $r\colon M \to C$
, we finally get a diagonal map
$r\colon M \to C$
, we finally get a diagonal map
This is the main protagonist of our construction. The diagonal map induces a homomorphism
![]() $f_* \colon \pi _1(M) \to \pi _1(S^1) = {\mathbb {Z}}$
. A dichotomy arises here:
$f_* \colon \pi _1(M) \to \pi _1(S^1) = {\mathbb {Z}}$
. A dichotomy arises here:

Figure 15 Every square (and, hence, every k-cube) of the cubulation has its opposite edges oriented coherently as shown here.
Proposition 12. Precisely one of the following holds:
-
(1) The facets of P with the same colour also have the same status. In this case, f is homotopic to a constant.
-
(2) There are at least two facets in P with equal colour and opposite status. In this case, the homomorphism
 $f_*\colon \pi _1(M) \to \pi _1(S^1) = {\mathbb {Z}}$
is nontrivial with image
$f_*\colon \pi _1(M) \to \pi _1(S^1) = {\mathbb {Z}}$
is nontrivial with image
 $2{\mathbb {Z}}$
.
$2{\mathbb {Z}}$
.
Proof. If (1) holds, all the edges joining two given vertices of C are oriented in the same way, and we may lift the map
![]() $f\colon M \to S^1$
to a map
$f\colon M \to S^1$
to a map
![]() $\tilde f \colon M \to {\mathbb {R}}$
as follows: send every vertex
$\tilde f \colon M \to {\mathbb {R}}$
as follows: send every vertex
![]() $v\in {\mathbb {Z}}_2^c$
of C to the maximum number of edges entering in v and pointing inward from distinct vertices, then extend
$v\in {\mathbb {Z}}_2^c$
of C to the maximum number of edges entering in v and pointing inward from distinct vertices, then extend
![]() $\tilde f$
diagonally to cubes. Since f can be lifted, it is homotopic to a constant.
$\tilde f$
diagonally to cubes. Since f can be lifted, it is homotopic to a constant.
If (2) holds, there are two edges joining the same pair of vertices with opposite orientation that form a loop that is sent to
![]() $\pm 2$
along
$\pm 2$
along
![]() $f_*$
. Moreover,
$f_*$
. Moreover,
![]() $1 \not \in \mathrm {Im}(f_*)$
because the 1-skeleton of C is naturally bipartited into even and odd vertices, according to the parity of
$1 \not \in \mathrm {Im}(f_*)$
because the 1-skeleton of C is naturally bipartited into even and odd vertices, according to the parity of
![]() $v_1+\cdots + v_c$
.
$v_1+\cdots + v_c$
.
The case (1) is not so interesting: All the examples that we construct here on the hyperbolic manifolds
![]() $M^n$
will be of type (2). In (2), since
$M^n$
will be of type (2). In (2), since
![]() $\mathrm {Im} f_* = 2 {\mathbb {Z}}$
, one may decide to replace f with a lift along a degree-2 covering of
$\mathrm {Im} f_* = 2 {\mathbb {Z}}$
, one may decide to replace f with a lift along a degree-2 covering of
![]() $S^1$
to get a surjective
$S^1$
to get a surjective
![]() $f_*$
.
$f_*$
.
Corollary 13. If all the facets of P have distinct colours, the diagonal map f is always homotopically trivial, for every choice of a state.
This inefficient colouring is therefore of no use here.
Example 14. For the 3-coloured
![]() $P^3$
, we will choose the following state: For every pair of faces with the same colour, assign I to one face and O to the other (the choice of which face gets I and which face gets O will not affect the result much, as we will see). The resulting 1-skeleton of C is then oriented as in Figure 16. By Proposition 12, the homomorphism
$P^3$
, we will choose the following state: For every pair of faces with the same colour, assign I to one face and O to the other (the choice of which face gets I and which face gets O will not affect the result much, as we will see). The resulting 1-skeleton of C is then oriented as in Figure 16. By Proposition 12, the homomorphism
![]() $f_*$
is not trivial.
$f_*$
is not trivial.

Figure 16 We assign a state to
![]() $P^3$
, where faces with the same colours have opposite status. We get the orientation of the 1-skeleton of C shown here.
$P^3$
, where faces with the same colours have opposite status. We get the orientation of the 1-skeleton of C shown here.
2.3 States and orbits
Let a right-angled
![]() $P\subset {\mathbb {X}}^n$
be equipped with a colouring and a state s. These determine a diagonal map
$P\subset {\mathbb {X}}^n$
be equipped with a colouring and a state s. These determine a diagonal map
![]() $f\colon M \to S^1$
as explained above. We now would like to study f and how it depends on s. A powerful machinery is already available for this task and is described by Bestvina and Brady in [Reference Bestvina and Brady7].
$f\colon M \to S^1$
as explained above. We now would like to study f and how it depends on s. A powerful machinery is already available for this task and is described by Bestvina and Brady in [Reference Bestvina and Brady7].
We call s the initial state. Recall that s induces a coherent orientation of the edges of the dual cubulation C. It also induces a state on every polytope
![]() $P_v$
of the tessellation, as follows: Every facet F of
$P_v$
of the tessellation, as follows: Every facet F of
![]() $P_v$
is dual to an edge e of C, and, hence, inherits a transverse orientation from that of e. We assign the status O or I to F according to whether the transverse orientation points outwards or inward with respect to
$P_v$
is dual to an edge e of C, and, hence, inherits a transverse orientation from that of e. We assign the status O or I to F according to whether the transverse orientation points outwards or inward with respect to
![]() $P_v$
. It is easy to see that the state induced on
$P_v$
. It is easy to see that the state induced on
![]() $P_v$
is precisely
$P_v$
is precisely
![]() $v(s)$
, the result of the action of v on the initial state s (as described in Section 2.1).
$v(s)$
, the result of the action of v on the initial state s (as described in Section 2.1).
Summing up, the polyhedron
![]() $P_0$
has the initial state s, while
$P_0$
has the initial state s, while
![]() $P_v$
inherits the state
$P_v$
inherits the state
![]() $v(s)$
for each
$v(s)$
for each
![]() $v\in {\mathbb {Z}}_2^c$
. The following proposition says that the states that lie in the same orbits produce equivalent diagonal maps.
$v\in {\mathbb {Z}}_2^c$
. The following proposition says that the states that lie in the same orbits produce equivalent diagonal maps.
Proposition 15. Two states
![]() $s,s'$
that lie in the same orbit with respect to the
$s,s'$
that lie in the same orbit with respect to the
![]() ${\mathbb {Z}}_2^c$
action produce two diagonal maps
${\mathbb {Z}}_2^c$
action produce two diagonal maps
![]() $f,f'\colon M \to S^1$
that are equivalent up to some isometry of M, that is there is an isometry
$f,f'\colon M \to S^1$
that are equivalent up to some isometry of M, that is there is an isometry
![]() $\psi \colon M \to M$
with
$\psi \colon M \to M$
with
![]() $f = f'\circ \psi $
.
$f = f'\circ \psi $
.
Proof. If
![]() $s' = w(s)$
for some
$s' = w(s)$
for some
![]() $w\in {\mathbb {Z}}_2^c$
, we pick the isometry
$w\in {\mathbb {Z}}_2^c$
, we pick the isometry
![]() $\psi \colon M \to M$
that sends
$\psi \colon M \to M$
that sends
![]() $P_v$
to
$P_v$
to
![]() $P_{v+w}$
via the identity map. We get
$P_{v+w}$
via the identity map. We get
![]() $f=f'\circ \psi $
.
$f=f'\circ \psi $
.
2.4 Ascending and descending links
Let a right-angled
![]() $P\subset {\mathbb {X}}^n$
be equipped with a state s. Let Q be a Euclidean polytope combinatorially dual to P. When
$P\subset {\mathbb {X}}^n$
be equipped with a state s. Let Q be a Euclidean polytope combinatorially dual to P. When
![]() $P=P^3, \ldots , P^8$
, of course Q is a Gosset polytope. The state s induces a dual state on Q, that is the assignment of a status I or O to each vertex of Q.
$P=P^3, \ldots , P^8$
, of course Q is a Gosset polytope. The state s induces a dual state on Q, that is the assignment of a status I or O to each vertex of Q.
If we remove the interiors of the
![]() $(n-1)$
-octahedral facets from
$(n-1)$
-octahedral facets from
![]() $\partial Q$
(that correspond to the ideal vertices of P), we are left with a flag simplicial complex
$\partial Q$
(that correspond to the ideal vertices of P), we are left with a flag simplicial complex
![]() $\dot Q$
. This holds because P is right-angled, and, hence, simple; as a consequence, every face of Q is a simplex, except the
$\dot Q$
. This holds because P is right-angled, and, hence, simple; as a consequence, every face of Q is a simplex, except the
![]() $(n-1)$
-octahedral facets dual to the ideal vertices of P.
$(n-1)$
-octahedral facets dual to the ideal vertices of P.
Following [Reference Bestvina and Brady7], we define the ascending link (respectively, descending link) as the subcomplex of
![]() $\dot Q$
generated by the vertices with status O (respectively, I). Since
$\dot Q$
generated by the vertices with status O (respectively, I). Since
![]() $\dot Q$
is a flag complex, these subcomplexes are determined by their 1-skeleton.
$\dot Q$
is a flag complex, these subcomplexes are determined by their 1-skeleton.
Let now P be equipped with both a colouring and a state. We get a manifold M and a diagonal map
![]() $f\colon M \to S^1$
. For every vertex
$f\colon M \to S^1$
. For every vertex
![]() $v\in {\mathbb {Z}}_2^c$
of the dual cubulation C, the link of v in C is precisely the simplicial complex
$v\in {\mathbb {Z}}_2^c$
of the dual cubulation C, the link of v in C is precisely the simplicial complex
![]() $ {\mathrm {link}}(v) = \dot Q$
, and it inherits the state
$ {\mathrm {link}}(v) = \dot Q$
, and it inherits the state
![]() $v(s)$
of
$v(s)$
of
![]() $P_v$
. The status of a vertex of
$P_v$
. The status of a vertex of
![]() $ {\mathrm {link}}(v)$
is I or O according to whether the corresponding oriented edge of C points inward or outward with respect to v. The ascending and descending links at v are denoted, respectively, as
$ {\mathrm {link}}(v)$
is I or O according to whether the corresponding oriented edge of C points inward or outward with respect to v. The ascending and descending links at v are denoted, respectively, as
![]() $ {\mathrm {link}}_\uparrow (v)$
and
$ {\mathrm {link}}_\uparrow (v)$
and
![]() $ {\mathrm {link}}_\downarrow (v)$
, and they are disjoint subcomplexes of
$ {\mathrm {link}}_\downarrow (v)$
, and they are disjoint subcomplexes of
![]() $ {\mathrm {link}}(v)$
.
$ {\mathrm {link}}(v)$
.
The diagonal map
![]() $f\colon M \to S^1$
induces a homomorphism
$f\colon M \to S^1$
induces a homomorphism
![]() $f_*\colon \pi _1(M) \to {\mathbb {Z}}$
. We are interested in its kernel H.
$f_*\colon \pi _1(M) \to {\mathbb {Z}}$
. We are interested in its kernel H.
Theorem 16 [Reference Bestvina and Brady7, Theorem 4.1]
The following holds:
-
• If
 $ {\mathrm {link}}_\uparrow (v)$
,
$ {\mathrm {link}}_\uparrow (v)$
,
 $ {\mathrm {link}}_\downarrow (v)$
are connected for every v, then H is finitely generated.
$ {\mathrm {link}}_\downarrow (v)$
are connected for every v, then H is finitely generated. -
• If
 $ {\mathrm {link}}_\uparrow (v)$
,
$ {\mathrm {link}}_\uparrow (v)$
,
 $ {\mathrm {link}}_\downarrow (v)$
are simply connected for every v, H is finitely presented.
$ {\mathrm {link}}_\downarrow (v)$
are simply connected for every v, H is finitely presented.
2.5 Legal states
Following [Reference Jankiewicz, Norin and Wise18], a state s on P is legal if the ascending and descending links that it determines on the dual flag simplicial complex
![]() $\dot Q$
are both connected. The group
$\dot Q$
are both connected. The group
![]() ${\mathbb {Z}}_2^c$
acts on the set of all states of P, and an orbit is legal if it consists only of legal states. As noted in [Reference Jankiewicz, Norin and Wise18], Theorem 16 implies the following.
${\mathbb {Z}}_2^c$
acts on the set of all states of P, and an orbit is legal if it consists only of legal states. As noted in [Reference Jankiewicz, Norin and Wise18], Theorem 16 implies the following.
Corollary 17. A legal orbit defines a diagonal map
![]() $f\colon M \to S^1$
with finitely generated
$f\colon M \to S^1$
with finitely generated
![]() $H= \ker f_*$
.
$H= \ker f_*$
.
The chase of a legal orbit is the combinatorial game introduced in [Reference Jankiewicz, Norin and Wise18]. After introducing the rules of the game, the authors exhibited some legal orbits on two remarkable right-angled polytopes in
![]() $ {\mathbb {H}}^4$
, namely, the ideal 24-cell and the compact right-angled 120-cell [Reference Jankiewicz, Norin and Wise18], so providing the first algebraically fibring hyperbolic 4-manifolds. Here, we play with the right-angled polytopes
$ {\mathbb {H}}^4$
, namely, the ideal 24-cell and the compact right-angled 120-cell [Reference Jankiewicz, Norin and Wise18], so providing the first algebraically fibring hyperbolic 4-manifolds. Here, we play with the right-angled polytopes
![]() $P^n$
and find some legal orbits on all of them. More than that, we find some even better kind of orbits in the cases
$P^n$
and find some legal orbits on all of them. More than that, we find some even better kind of orbits in the cases
![]() $n=3,7,8$
, that we call 1-legal.
$n=3,7,8$
, that we call 1-legal.
2.6 1-legal states
We extend the nomenclature of [Reference Jankiewicz, Norin and Wise18] by saying that a state s is 1-legal if its ascending and descending links are both simply connected. An orbit is 1-legal if it consists only of 1-legal state. Here is a consequence of Theorem 16.
Corollary 18. A 1-legal orbit defines a diagonal map
![]() $f\colon M \to S^1$
with finitely presented
$f\colon M \to S^1$
with finitely presented
![]() $H= \ker f_*$
.
$H= \ker f_*$
.
2.7 The Euler characteristic check
In the following pages, we will double count the Euler characteristic of our manifolds as a safety check. If a colouring and a state on P produce a manifold M and a diagonal function
![]() $f\colon M \to S^1$
, we always have
$f\colon M \to S^1$
, we always have
The same formula holds with the descending link
![]() $ {\mathrm {link}}_{\downarrow }(v)$
. We say that the integer
$ {\mathrm {link}}_{\downarrow }(v)$
. We say that the integer
![]() $1-\chi ( {\mathrm {link}}_\uparrow (v))$
is the contribution of v to the Euler characteristic of M. Note that a contractible ascending link contributes with zero, while a k-sphere contributes with
$1-\chi ( {\mathrm {link}}_\uparrow (v))$
is the contribution of v to the Euler characteristic of M. Note that a contractible ascending link contributes with zero, while a k-sphere contributes with
![]() $(-1)^{k+1}$
.
$(-1)^{k+1}$
.
We now construct a legal orbit on each individual polytope
![]() $P^3, \ldots , P^8$
. We have used a code written with Sage to analyse all these cases; both the code and the resulting data are available from [Reference Martelli39].
$P^3, \ldots , P^8$
. We have used a code written with Sage to analyse all these cases; both the code and the resulting data are available from [Reference Martelli39].
2.8 A 1-legal orbit for
 $P^3$
$P^3$
In the 3-colouring of
![]() $P^3$
, the facets are partitioned into three pairs. For every pair, we assign the status O to one facet and I to the other, arbitrarily. The orbit of this state s is independent of this choice and consists precisely of all the
$P^3$
, the facets are partitioned into three pairs. For every pair, we assign the status O to one facet and I to the other, arbitrarily. The orbit of this state s is independent of this choice and consists precisely of all the
![]() $2^3=8$
states that can be constructed in this way.
$2^3=8$
states that can be constructed in this way.
By direct inspection, we find that the eight states reduce to two up to isomorphism, and they are shown in Figure 17. The ascending and descending links are both either a triangle or two segments connected along an endpoint. In both cases, they are contractible. One can, in fact, verify that the conditions of [Reference Battista and Martelli6, Theorem 15] are satisfied, and, hence, the diagonal map
![]() $f\colon M^3 \to S^1$
can be smoothened to become a fibration (we will not need this here).
$f\colon M^3 \to S^1$
can be smoothened to become a fibration (we will not need this here).

Figure 17 We exhibit a state by colouring the vertices in black and white, with black (white) corresponding to the status I (O). There are only two states in the orbit of
![]() $P^3$
up to isomorphism, and in both cases, the ascending and descending links are contractible: they are a triangle and two segments joined along an endpoint.
$P^3$
up to isomorphism, and in both cases, the ascending and descending links are contractible: they are a triangle and two segments joined along an endpoint.
The ascending and descending links are simply connected, and, hence, the orbit is 1-legal. By Corollary 18, the kernel H of
![]() $f_*\colon \pi _1(M^3) \to {\mathbb {Z}}$
is finitely presented: It is the fundamental group of the surface fibre of the fibration
$f_*\colon \pi _1(M^3) \to {\mathbb {Z}}$
is finitely presented: It is the fundamental group of the surface fibre of the fibration
![]() $f\colon M^3 \to S^1$
.
$f\colon M^3 \to S^1$
.
The formula (1) holds since
![]() $\chi (M^3)=0$
and each contractible link contributes with zero to the sum.
$\chi (M^3)=0$
and each contractible link contributes with zero to the sum.
2.9 A legal orbit for
 $P^4$
$P^4$
In the 5-colouring of
![]() $P^4$
, the facets are partitioned into five pairs. As in the previous case, we assign the statuses O and I arbitrarily to each pair. The orbit consists of all the states that assign distinct statuses to each pair. We get
$P^4$
, the facets are partitioned into five pairs. As in the previous case, we assign the statuses O and I arbitrarily to each pair. The orbit consists of all the states that assign distinct statuses to each pair. We get
![]() $2^5=32$
states.
$2^5=32$
states.
By direct inspection, we find that these states reduce to four up to isomorphism, depicted in Figure 18. As shown in the figure, the ascending and descending links are always connected, so the orbit is legal. However, we note that the orbit is not 1-legal, since in the first case, both the ascending and descending links are circles. The first case occurs only in two of the 32 states.

Figure 18 We exhibit a state by colouring the vertices in black and white, with black (white) corresponding to the status I (O). There are only four states in the orbit of
![]() $P^4$
up to isomorphism. We show here the descending link, generated by the black vertices. In the first case, we get a circle, while in the other cases, we always get a contractible complex made of three triangles, two triangles and one tetrahedron and one triangle, respectively. The ascending links are of the same types.
$P^4$
up to isomorphism. We show here the descending link, generated by the black vertices. In the first case, we get a circle, while in the other cases, we always get a contractible complex made of three triangles, two triangles and one tetrahedron and one triangle, respectively. The ascending links are of the same types.
In fact, one can verify that the ascending and descending links in the first case form a Hopf link in
![]() $S^3$
, if considered in the boundary of the Gosset polytope, and that the conditions of [Reference Battista and Martelli6, Theorem 15] are satisfied, so the diagonal function
$S^3$
, if considered in the boundary of the Gosset polytope, and that the conditions of [Reference Battista and Martelli6, Theorem 15] are satisfied, so the diagonal function
![]() $f\colon M^4 \to S^1$
can be smoothened to a circle-valued Morse function with two index-2 critical points. This is the best that we can get in dimension 4, since no fibrations may occur on an even-dimensional hyperbolic manifold (we will not need these facts here, for more details see [Reference Battista and Martelli6]).
$f\colon M^4 \to S^1$
can be smoothened to a circle-valued Morse function with two index-2 critical points. This is the best that we can get in dimension 4, since no fibrations may occur on an even-dimensional hyperbolic manifold (we will not need these facts here, for more details see [Reference Battista and Martelli6]).
By Corollary 17, the kernel H of
![]() $f_*\colon \pi _1(M^4) \to {\mathbb {Z}}$
is finitely generated. The formula (1) holds since
$f_*\colon \pi _1(M^4) \to {\mathbb {Z}}$
is finitely generated. The formula (1) holds since
![]() $\chi (M^4)=2$
and the two states of the first kind contribute each with 1, while all the others contribute with 0.
$\chi (M^4)=2$
and the two states of the first kind contribute each with 1, while all the others contribute with 0.
2.10 A legal orbit for
 $P^5$
$P^5$
In the 8-colouring for
![]() $P^5$
, the facets are partitioned into eight pairs. As in the previous cases, we assign the statuses O and I arbitrarily to each pair. The orbit consists of all the states that assign different statuses to each pair. We get
$P^5$
, the facets are partitioned into eight pairs. As in the previous cases, we assign the statuses O and I arbitrarily to each pair. The orbit consists of all the states that assign different statuses to each pair. We get
![]() $2^8 = 256$
states.
$2^8 = 256$
states.
Each state produces a pair of ascending and descending links. Since these are flag simplicial complexes, they are determined by their 1-skeleta. Either using our program with Sage or by direct inspection, we find that the resulting 512 graphs reduce to only seven up to isomorphism. These seven graphs are those generated by the black vertices in Figure 19.

Figure 19 Every ascending or descending link for
![]() $P^5$
is isomorphic to one of the seven descending links shown here.
$P^5$
is isomorphic to one of the seven descending links shown here.
We can check by hand (or with our Sage program) that the first four graphs in the figure generate a contractible simplicial complex. The remaining three generate a simplicial complex that collapses, respectively, to
![]() $S^2$
, a wedge of three circles
$S^2$
, a wedge of three circles
![]() $\vee _3 S^1$
and
$\vee _3 S^1$
and
![]() $S^3$
. The complexes that collapse to
$S^3$
. The complexes that collapse to
![]() $S^2$
and
$S^2$
and
![]() $\vee _3 S^1$
are shown in Figure 20. The complex that collapses to
$\vee _3 S^1$
are shown in Figure 20. The complex that collapses to
![]() $S^3$
is actually homeomorphic to
$S^3$
is actually homeomorphic to
![]() $S^3$
, and it is the boundary of a 4-octahedron, decomposed into 16 tetrahedra. It corresponds dually to an ideal vertex of
$S^3$
, and it is the boundary of a 4-octahedron, decomposed into 16 tetrahedra. It corresponds dually to an ideal vertex of
![]() $P^5$
.
$P^5$
.
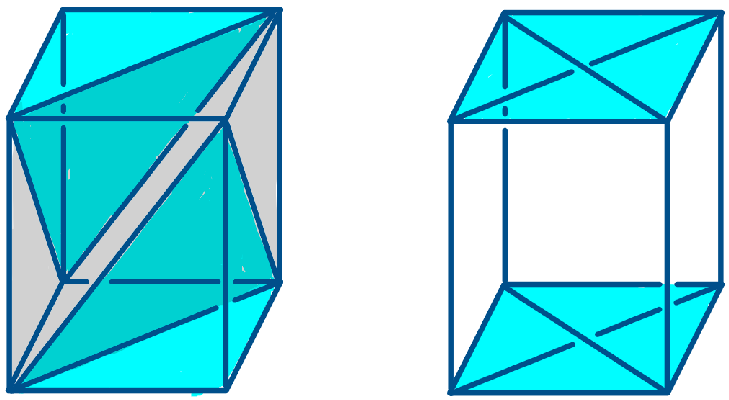
Figure 20 Two simplicial complexes that collapse to
![]() $S^2$
and
$S^2$
and
![]() $\vee _3 S^1$
. The first is the boundary of an octahedron with two tetrahedra attached to a pair of opposite faces. The second consists of two tetrahedra and four edges joining them.
$\vee _3 S^1$
. The first is the boundary of an octahedron with two tetrahedra attached to a pair of opposite faces. The second consists of two tetrahedra and four edges joining them.
In all the cases, the simplcial complex is connected, so the orbit is legal. It is not always simply connected, so the orbit is not 1-legal. By Corollary 17, the kernel H of
![]() $f_*\colon \pi _1(M^5) \to {\mathbb {Z}}$
is finitely generated.
$f_*\colon \pi _1(M^5) \to {\mathbb {Z}}$
is finitely generated.
The formula (1) holds since
![]() $\chi (M^5)=0$
, and using Sage, we find that we get 32 occurrences of
$\chi (M^5)=0$
, and using Sage, we find that we get 32 occurrences of
![]() $S^2$
, eight of
$S^2$
, eight of
![]() $\vee _3 S^1$
and eight of
$\vee _3 S^1$
and eight of
![]() $S^3$
. Their contributions to the Euler characteristic are
$S^3$
. Their contributions to the Euler characteristic are
![]() $32\cdot (-1) + 8\cdot 3 + 8 \cdot 1 = 0$
.
$32\cdot (-1) + 8\cdot 3 + 8 \cdot 1 = 0$
.
2.11 A legal orbit for
 $P^6$
$P^6$
In the 9-colouring for
![]() $P^6$
, the 27 facets are partitioned into nine triplets. As opposite to the previous cases, there does not seem to be a natural choice of a state here. However, a brute computer search shows that there are many legal orbits for
$P^6$
, the 27 facets are partitioned into nine triplets. As opposite to the previous cases, there does not seem to be a natural choice of a state here. However, a brute computer search shows that there are many legal orbits for
![]() $P^6$
. For instance, we may take s as the state where the first vertex in each triple listed in Section 1.11 is O and the remaining two are I. By using our Sage program, we find that the orbit of this state is legal. By Corollary 17, the kernel H of
$P^6$
. For instance, we may take s as the state where the first vertex in each triple listed in Section 1.11 is O and the remaining two are I. By using our Sage program, we find that the orbit of this state is legal. By Corollary 17, the kernel H of
![]() $f_*\colon \pi _1(M^6) \to {\mathbb {Z}}$
is finitely generated.
$f_*\colon \pi _1(M^6) \to {\mathbb {Z}}$
is finitely generated.
As we said, a computer search shows that many initial states s yield legal orbits. We could not find a single 1-legal orbit, but, admittedly, we have not checked all the possible initial states.
2.12 A 1-legal orbit for
 $P^7$
$P^7$
In the 14-colouring for
![]() $P^7$
, the 56 facets are partitioned into 14 quartets. We see
$P^7$
, the 56 facets are partitioned into 14 quartets. We see
![]() $P^7$
as the facet of
$P^7$
as the facet of
![]() $P^8$
dual to the vertex
$P^8$
dual to the vertex
![]() $1$
in
$1$
in
![]() $4_{21}$
. We will define below a state for
$4_{21}$
. We will define below a state for
![]() $P^8$
, and this will induce one s for
$P^8$
, and this will induce one s for
![]() $P^7$
in the obvious way: every facet of
$P^7$
in the obvious way: every facet of
![]() $P^7$
inherits the status of the adjacent facet in
$P^7$
inherits the status of the adjacent facet in
![]() $P^8$
.
$P^8$
.
The state s inherited in this way turns out to be balanced with respect to the colouring, in the following sense: There is an even number
![]() $2m$
of facets sharing the same colour, and precisely half of them m are given the status I, and the other half m the status O. If a state is balanced, then every other state in the orbit is also balanced. The states that we have chosen for
$2m$
of facets sharing the same colour, and precisely half of them m are given the status I, and the other half m the status O. If a state is balanced, then every other state in the orbit is also balanced. The states that we have chosen for
![]() $P^3, P^4$
and
$P^3, P^4$
and
![]() $P^5$
are balanced: For these polyhedra, we have
$P^5$
are balanced: For these polyhedra, we have
![]() $m=1$
, and there was, in fact, a unique orbit of balanced states. Here,
$m=1$
, and there was, in fact, a unique orbit of balanced states. Here,
![]() $m=2$
, so in each quartet, two facets receive the status I and two the status O.
$m=2$
, so in each quartet, two facets receive the status I and two the status O.
The orbit of s consists of
![]() $2^{14}$
states, each contributing with an ascending and descending link. Using Sage, we are pleased to discover that the resulting
$2^{14}$
states, each contributing with an ascending and descending link. Using Sage, we are pleased to discover that the resulting
![]() $2^{15} = 32,768$
graphs reduce to only 106 up to isomorphism (this is probably due to the many symmetries of s that are inherited from
$2^{15} = 32,768$
graphs reduce to only 106 up to isomorphism (this is probably due to the many symmetries of s that are inherited from
![]() $P^8$
).
$P^8$
).
Using Sage, we also see that all the simplicial complexes generated by the 106 graphs are simply connected. Therefore, the orbit is 1-legal. With Sage, we have also checked (1). All the data can be found in [Reference Martelli39]. By Corollary 18, the kernel H of
![]() $f_*\colon \pi _1(M^7) \to {\mathbb {Z}}$
is finitely presented.
$f_*\colon \pi _1(M^7) \to {\mathbb {Z}}$
is finitely presented.
2.13 A 1-legal orbit for
 $P^8$
$P^8$
In the 15-colouring for
![]() $P^8$
, the 240 facets are partitioned into 15 hextets. How can we find a good initial state s for
$P^8$
, the 240 facets are partitioned into 15 hextets. How can we find a good initial state s for
![]() $P^8$
? The numbers are overwhelming: the polytope
$P^8$
? The numbers are overwhelming: the polytope
![]() $P^8$
has 240 facets, so there are
$P^8$
has 240 facets, so there are
![]() $2^{240}$
possible states to choose from. Each orbit consists of
$2^{240}$
possible states to choose from. Each orbit consists of
![]() $2^{15}$
distinct states, and we would like to find one orbit where all these
$2^{15}$
distinct states, and we would like to find one orbit where all these
![]() $2^{15}$
states are legal, or even better, 1-legal. A brute force computer search is out of reach.
$2^{15}$
states are legal, or even better, 1-legal. A brute force computer search is out of reach.
To define a legal state, we take inspiration from the 24-cell sitting inside quaternions space, since this has some strong analogies with the Gosset polytope
![]() $4_{21}$
sitting in octonions space as we already noticed above. We have already exploited this analogy when we fixed a convenient colouring for
$4_{21}$
sitting in octonions space as we already noticed above. We have already exploited this analogy when we fixed a convenient colouring for
![]() $P^8$
, and we do it again now to design a convenient state.
$P^8$
, and we do it again now to design a convenient state.
A state for the 24-cell
A nice legal state for the 24-cell was constructed in [Reference Battista and Martelli6] as follows. Recall that its 24 vertices are divided into three octets: these are
![]() $ \pm 1, \pm i, \pm j, \pm k$
, the elements
$ \pm 1, \pm i, \pm j, \pm k$
, the elements
![]() $\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an even number of minus signs and those with an odd number of minus signs.
$\tfrac 12 (\pm 1 \pm i \pm j \pm k) $
with an even number of minus signs and those with an odd number of minus signs.
Consider the group
![]() $G=\{\pm 1, \pm i\}$
and its action on the 24 vertices by left-multiplication. We can verify easily that each octet is invariant by this action, and is subdivided into two orbits of four elements each. We assign arbitrarily the status I to one orbit, and O to the other. The resulting state s is balanced (see the definition above), and also legal, as it was, in fact, already observed in [Reference Jankiewicz, Norin and Wise18]. The ascending and descending links are each homeomorphic to a G-invariant annulus as in Figure 21, so they are connected but not simply connected (the state is not 1-legal). The two G-invariant annuli form altogether a banded Hopf link in
$G=\{\pm 1, \pm i\}$
and its action on the 24 vertices by left-multiplication. We can verify easily that each octet is invariant by this action, and is subdivided into two orbits of four elements each. We assign arbitrarily the status I to one orbit, and O to the other. The resulting state s is balanced (see the definition above), and also legal, as it was, in fact, already observed in [Reference Jankiewicz, Norin and Wise18]. The ascending and descending links are each homeomorphic to a G-invariant annulus as in Figure 21, so they are connected but not simply connected (the state is not 1-legal). The two G-invariant annuli form altogether a banded Hopf link in
![]() $S^3$
.
$S^3$
.

Figure 21 The ascending and descending links are both an annulus decomposed into 12 triangles, and altogether, they form two annuli that collapse onto a Hopf link in
![]() $S^3$
. The figure (taken from [Reference Battista and Martelli6]) shows the vertices of the 24-cell, with their 3-colouring (Blue / Red / Yellow) and their state (the vertices with a O status have an additional black circle). Only some edges of the 24-cell are shown for the sake of clarity: more edges should be added that connect each yellow vertex and its eight neighbours.
$S^3$
. The figure (taken from [Reference Battista and Martelli6]) shows the vertices of the 24-cell, with their 3-colouring (Blue / Red / Yellow) and their state (the vertices with a O status have an additional black circle). Only some edges of the 24-cell are shown for the sake of clarity: more edges should be added that connect each yellow vertex and its eight neighbours.
The orbit of s along the action of
![]() ${\mathbb {Z}}_2^3$
consists of the
${\mathbb {Z}}_2^3$
consists of the
![]() $2^3$
states obtained from s by reversing the I/O status of some octet. The geometry of the 24-cell is so extraordinary that these
$2^3$
states obtained from s by reversing the I/O status of some octet. The geometry of the 24-cell is so extraordinary that these
![]() $2^3$
states are all isomorphic [Reference Battista and Martelli6]. In particular, the orbit is legal (but it is not 1-legal). The choice of which orbit is I and which is O inside each octet is irrelevant, since different choices lead to the same orbit.
$2^3$
states are all isomorphic [Reference Battista and Martelli6]. In particular, the orbit is legal (but it is not 1-legal). The choice of which orbit is I and which is O inside each octet is irrelevant, since different choices lead to the same orbit.
A state for
 $4_{21}$
$4_{21}$
We now try to mimic the above construction for
![]() $4_{21}$
. The 240 vertices are partitioned into 15 hextets, that is
$4_{21}$
. The 240 vertices are partitioned into 15 hextets, that is
![]() $\pm 1,\pm e_1, \pm e_2, \pm e_3, \pm e_4, \pm e_5, \pm e_6, \pm e_7$
, the elements
$\pm 1,\pm e_1, \pm e_2, \pm e_3, \pm e_4, \pm e_5, \pm e_6, \pm e_7$
, the elements
![]() $\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
$\tfrac 12(\pm 1 \pm e_{n} \pm e_{n+1} \pm e_{n+3})$
and
![]() $\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an even number of minus signs, and those with an odd number of minus signs, with the integer n varying modulo 7.
$\tfrac 12(\pm e_{n+2} \pm e_{n+4} \pm e_{n+5} \pm e_{n+6})$
with an even number of minus signs, and those with an odd number of minus signs, with the integer n varying modulo 7.
It is now natural to consider the quaternion group
![]() $Q = \{ \pm 1, \pm e_1, \pm e_2, \pm e_4\}$
and its ‘action’ on the 240 vertices of
$Q = \{ \pm 1, \pm e_1, \pm e_2, \pm e_4\}$
and its ‘action’ on the 240 vertices of
![]() $4_{21}$
by left-multiplication. This is the analogue of the group
$4_{21}$
by left-multiplication. This is the analogue of the group
![]() $G=\{\pm 1, \pm i\}$
defined above, roughly because taking quaternions inside octonions looks like taking complex numbers inside quaternions. However, this is not really a group action because octonions are not associative, and, hence, we may have that
$G=\{\pm 1, \pm i\}$
defined above, roughly because taking quaternions inside octonions looks like taking complex numbers inside quaternions. However, this is not really a group action because octonions are not associative, and, hence, we may have that
![]() $e_1(e_2(x)) \neq (e_1e_2)(x)$
. Therefore, some caution is needed.
$e_1(e_2(x)) \neq (e_1e_2)(x)$
. Therefore, some caution is needed.
We already know that the set
![]() $S=\{\pm 1, \pm e_1, \ldots , \pm e_7\}$
acts freely and transitively by left-multiplication on every hextet (that is, for every pair of elements in the hextet, there is a unique element in S whose left-multiplication sends the first to the second). We pick the following 15 base elements, one inside each hextet:
$S=\{\pm 1, \pm e_1, \ldots , \pm e_7\}$
acts freely and transitively by left-multiplication on every hextet (that is, for every pair of elements in the hextet, there is a unique element in S whose left-multiplication sends the first to the second). We pick the following 15 base elements, one inside each hextet:
where n runs modulo 7. We consider inside each hextet the eight elements obtained by left-multiplying the base element by the elements of Q. We assign to these eight elements the status O, and the status I to the remaining eight of the hextet. We have defined a balanced state s. The orbit consists of
![]() $2^{15}$
balanced states.
$2^{15}$
balanced states.
Remark 19. By analogy with the 24-cell, it would be tempting to guess that the
![]() $2^{15}$
states in the orbit are all isomorphic, and maybe that the ascending and descending links are homotopic to two copies of
$2^{15}$
states in the orbit are all isomorphic, and maybe that the ascending and descending links are homotopic to two copies of
![]() $S^3$
linked in
$S^3$
linked in
![]() $S^7$
. This is, however, impossible by a Euler characteristic argument, due to the fact that the 24-cell has
$S^7$
. This is, however, impossible by a Euler characteristic argument, due to the fact that the 24-cell has
![]() $\chi = 1$
, while
$\chi = 1$
, while
![]() $\chi (P^8) = 17/2$
is much bigger. In general, one should not push the analogies too far: The situation is intrinsically more complicated here. We will come back to this point below.
$\chi (P^8) = 17/2$
is much bigger. In general, one should not push the analogies too far: The situation is intrinsically more complicated here. We will come back to this point below.
Using our Sage code, we have determined the ascending and descending links of each of the
![]() $2^{15} = 32,768$
states. Note that each graph can have up to 240 vertices, and we have
$2^{15} = 32,768$
states. Note that each graph can have up to 240 vertices, and we have
![]() $2^{16} = 65,536$
graphs to analyse. Luckily, these graphs reduce up to isomorphism to only 185. This is probably due to the extraordinary symmetries of both the colouring and the state that we have chosen for
$2^{16} = 65,536$
graphs to analyse. Luckily, these graphs reduce up to isomorphism to only 185. This is probably due to the extraordinary symmetries of both the colouring and the state that we have chosen for
![]() $P^8$
. Our Sage program says that each of the 185 simplicial complexes generated by these graphs is connected and simply connected. Therefore, the orbit is 1-legal. By Corollary 18, the kernel H of
$P^8$
. Our Sage program says that each of the 185 simplicial complexes generated by these graphs is connected and simply connected. Therefore, the orbit is 1-legal. By Corollary 18, the kernel H of
![]() $f_*\colon \pi _1(M^8) \to {\mathbb {Z}}$
is finitely presented.
$f_*\colon \pi _1(M^8) \to {\mathbb {Z}}$
is finitely presented.
Remark 20. We also checked (1). Both sides give (quite reassuringly) the same number
![]() $278,528$
. The formula (1) also explains a fact we alluded to in Remark 19. Since
$278,528$
. The formula (1) also explains a fact we alluded to in Remark 19. Since
![]() $\chi (P^8) = 17/2$
, the average contribution to the Euler characteristic of an ascending link is
$\chi (P^8) = 17/2$
, the average contribution to the Euler characteristic of an ascending link is
![]() $17/2$
, which is a relatively big number if compared to the Euler characteristic of the other polytopes considered above. Referring to Remark 19, we note that it is certainly impossible that all the ascending links be
$17/2$
, which is a relatively big number if compared to the Euler characteristic of the other polytopes considered above. Referring to Remark 19, we note that it is certainly impossible that all the ascending links be
![]() $S^3$
, since their individual contribution would be 1. The ascending links that we find with Sage are indeed quite complicated (they are typically some wedges of spheres of various dimensions
$S^3$
, since their individual contribution would be 1. The ascending links that we find with Sage are indeed quite complicated (they are typically some wedges of spheres of various dimensions
![]() $k\geq 2$
), much more than those discovered with
$k\geq 2$
), much more than those discovered with
![]() $P^3,\ldots , P^7$
. They can be found in [Reference Martelli39].
$P^3,\ldots , P^7$
. They can be found in [Reference Martelli39].
2.14 The restriction of
 $f$
to the cusps
$f$
to the cusps
In our analysis, we have briefly mentioned the fact that when
![]() $n=3,4$
, the chosen orbits satisfy the conditions of [Reference Battista and Martelli6, Theorem 15] and, hence,
$n=3,4$
, the chosen orbits satisfy the conditions of [Reference Battista and Martelli6, Theorem 15] and, hence,
![]() $f\colon M^n \to S^1$
can be smoothened to become a perfect smooth circle-valued Morse function (for
$f\colon M^n \to S^1$
can be smoothened to become a perfect smooth circle-valued Morse function (for
![]() $n=3$
, this is a fibration).
$n=3$
, this is a fibration).
One may wonder if this is also the case when
![]() $n\geq 5$
, and, indeed, this was our hope at the beginning of our study: It would be extremely interesting to find a fibration on an odd-dimensional hyperbolic manifold of dimension 5 or 7. We show that this is not the case, for any possible choice of initial state, a serious obstruction being the restriction of f to the cusps of
$n\geq 5$
, and, indeed, this was our hope at the beginning of our study: It would be extremely interesting to find a fibration on an odd-dimensional hyperbolic manifold of dimension 5 or 7. We show that this is not the case, for any possible choice of initial state, a serious obstruction being the restriction of f to the cusps of
![]() $M^n$
.
$M^n$
.
Proposition 21. For
![]() $n=5, \ldots , 8$
, there is some cusp
$n=5, \ldots , 8$
, there is some cusp
![]() $X\cong T^{n-1} \times [0, + \infty ) \subset M^n$
, where the restriction
$X\cong T^{n-1} \times [0, + \infty ) \subset M^n$
, where the restriction
![]() $f|_X$
is homotopic to a constant. This holds for any possible choice of a state for
$f|_X$
is homotopic to a constant. This holds for any possible choice of a state for
![]() $P^n$
.
$P^n$
.
Proof. Let s be any initial state for
![]() $P^n$
. In our discussion above, we have said that when
$P^n$
. In our discussion above, we have said that when
![]() $n=5,7,8$
, there is always some ideal vertex v of
$n=5,7,8$
, there is always some ideal vertex v of
![]() $P^n$
whose link C is an
$P^n$
whose link C is an
![]() $(n-1)$
-cube coloured with
$(n-1)$
-cube coloured with
![]() $2(n-1)$
distinct colours. Let
$2(n-1)$
distinct colours. Let
![]() $T\subset M^n$
be a torus section that lies above C. The restriction of f to T is determined by the restriction of the state s of
$T\subset M^n$
be a torus section that lies above C. The restriction of f to T is determined by the restriction of the state s of
![]() $P^n$
to T. No matter what the restriction of s looks like, by Corollary 13, the restriction of f to T is homotopically trivial, and, hence, it is so on the cusp
$P^n$
to T. No matter what the restriction of s looks like, by Corollary 13, the restriction of f to T is homotopically trivial, and, hence, it is so on the cusp
![]() $X = T \times [0, + \infty )$
that it bounds.
$X = T \times [0, + \infty )$
that it bounds.
The case
![]() $n=6$
is a bit more involved. When
$n=6$
is a bit more involved. When
![]() $n=6$
, each of the 27 ideal vertices v has a 9-coloured 5-cube link C. This implies that there exists exactly one pair of opposite facets sharing the same colour. In each of the nine triplets of
$n=6$
, each of the 27 ideal vertices v has a 9-coloured 5-cube link C. This implies that there exists exactly one pair of opposite facets sharing the same colour. In each of the nine triplets of
![]() $P^6$
, every pair is an opposite pair of facets of this kind, for some ideal vertex v (we get
$P^6$
, every pair is an opposite pair of facets of this kind, for some ideal vertex v (we get
![]() $3\times 9 = 27$
pairs for
$3\times 9 = 27$
pairs for
![]() $27$
ideal vertices). For any choice of a state, there will be one such pair with the same status, because the three statuses on a triple cannot be all distinct. By Proposition 12, the restriction of f to this cusp is null-homotopic.
$27$
ideal vertices). For any choice of a state, there will be one such pair with the same status, because the three statuses on a triple cannot be all distinct. By Proposition 12, the restriction of f to this cusp is null-homotopic.
After writing a first draft of this paper, we found a fibration for
![]() $M^5$
with a more elaborated construction that overcomes this problem (see [Reference Italiano, Martelli and Migliorini17]).
$M^5$
with a more elaborated construction that overcomes this problem (see [Reference Italiano, Martelli and Migliorini17]).
2.15 The geometrically infinite coverings
For every
![]() $n=3, \ldots , 8$
, the kernel of
$n=3, \ldots , 8$
, the kernel of
![]() $f_*\colon \pi _1(M^n) \to \pi _1(S^1) = {\mathbb {Z}}$
is a normal subgroup
$f_*\colon \pi _1(M^n) \to \pi _1(S^1) = {\mathbb {Z}}$
is a normal subgroup
![]() $H\triangleleft \pi _1(M^n)$
of infinite index. We summarise our discoveries.
$H\triangleleft \pi _1(M^n)$
of infinite index. We summarise our discoveries.
Theorem 22. The normal subgroup H is finitely generated, and also finitely presented when
![]() $n=3,7,8$
. The limit set of H is the whole sphere
$n=3,7,8$
. The limit set of H is the whole sphere
![]() $\partial {\mathbb {H}}^n = S^{n-1}$
.
$\partial {\mathbb {H}}^n = S^{n-1}$
.
The limit set is the whole sphere because H is normal in
![]() $\pi _1(M^n)$
and
$\pi _1(M^n)$
and
![]() $M^n$
has finite volume. In particular, the hyperbolic n-manifold
$M^n$
has finite volume. In particular, the hyperbolic n-manifold
that covers
![]() $M^n$
is geometrically infinite. The dimension
$M^n$
is geometrically infinite. The dimension
![]() $n=4$
was investigated in [Reference Battista and Martelli6]. Here, we are particularly interested in the dimensions
$n=4$
was investigated in [Reference Battista and Martelli6]. Here, we are particularly interested in the dimensions
![]() $n=5,\ldots , 8$
.
$n=5,\ldots , 8$
.
Theorem 23. When
![]() $5\leq n \leq 8$
, the hyperbolic manifold
$5\leq n \leq 8$
, the hyperbolic manifold
![]() $\widetilde M^n$
has infinitely many toric cusps. In particular, the Betti number
$\widetilde M^n$
has infinitely many toric cusps. In particular, the Betti number
![]() $b_{n-1}(\widetilde M^n) = \infty $
is infinite and
$b_{n-1}(\widetilde M^n) = \infty $
is infinite and
![]() $\pi _1(\widetilde M^n)=H$
is not
$\pi _1(\widetilde M^n)=H$
is not
![]() $\mathrm { F}_{n-1}$
.
$\mathrm { F}_{n-1}$
.
Proof. The restriction of f to some cusp is null-homotopic by Proposition 21. Therefore, the cusp lifts to infinitely many copies of itself in
![]() $\widetilde M^n$
.
$\widetilde M^n$
.
Recall that a group H is of type
![]() $\mathrm {F}_m$
if there exists a
$\mathrm {F}_m$
if there exists a
![]() $K(H,1)$
with finite m-skeleton [Reference Bestvina and Brady7]. If H is
$K(H,1)$
with finite m-skeleton [Reference Bestvina and Brady7]. If H is
![]() $\mathrm {F}_m$
, the Betti number
$\mathrm {F}_m$
, the Betti number
![]() $b_m(H)$
is obviously finite.
$b_m(H)$
is obviously finite.
Corollary 24. When
![]() $n=7,8$
, the fundamental group of the hyperbolic manifold
$n=7,8$
, the fundamental group of the hyperbolic manifold
![]() $\widetilde M^n$
is finitely presented but not
$\widetilde M^n$
is finitely presented but not
![]() $\mathrm {F}_{n-1}$
.
$\mathrm {F}_{n-1}$
.
Competing Interests
None.