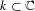Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Landesman, Aaron
Swaminathan, Ashvin
Tao, James
and
Xu, Yujie
2019.
Surjectivity of Galois representations in rational families of abelian varieties.
Algebra & Number Theory,
Vol. 13,
Issue. 5,
p.
995.
Baldi, Gregorio
2019.
Local to global principle for the moduli space of K3 surfaces.
Archiv der Mathematik,
Vol. 112,
Issue. 6,
p.
599.
Sutherland, Andrew V.
2019.
A database of nonhyperelliptic genus-3 curves
over ℚ.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
443.
Hui, Chun Yin
and
Larsen, Michael
2020.
Maximality of Galois actions for abelian and hyper-Kähler varieties.
Duke Mathematical Journal,
Vol. 169,
Issue. 6,
Frei, Sarah
Hassett, Brendan
and
Várilly-Alvarado, Anthony
2022.
Reduction of Brauer classes on K3 surfaces, rationality and derived equivalence.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 792,
p.
289.
Richard, Rodolphe
and
Yafaev, Andrei
2023.
On the generalised André–Pink–Zannier conjecture..
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G11,
p.
1717.
Hui, Chun Yin
2023.
Monodromy of subrepresentations and irreducibility of low degree automorphic Galois representations.
Journal of the London Mathematical Society,
Vol. 108,
Issue. 6,
p.
2436.
Lopuhaä-Zwakenberg, Milan
2024.
Integral models of reductive groups and integral Mumford–Tate groups.
Annales Henri Lebesgue,
Vol. 7,
Issue. ,
p.
749.
Richard, Rodolphe
and
Yafaev, Andrei
2024.
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture.
Compositio Mathematica,
Vol. 160,
Issue. 11,
p.
2531.
Valloni, Domenico
2024.
Rational Points in the Noether-Lefschetz Locus of Moduli Spaces of K3 Surfaces.
International Mathematics Research Notices,
Vol. 2024,
Issue. 14,
p.
10503.
ACHTER, JEFFREY D.
DUAN, LIAN
and
WANG, XIYUAN
2024.
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS.
Nagoya Mathematical Journal,
Vol. 253,
Issue. ,
p.
91.