Article contents
MODULI OF CURVES WITH NONSPECIAL DIVISORS AND RELATIVE MODULI OF 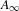 $A_{\infty }$-STRUCTURES
$A_{\infty }$-STRUCTURES
Published online by Cambridge University Press: 30 October 2017
Abstract
Inthis paper, for each 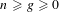 $n\geqslant g\geqslant 0$ we consider the moduli stack
$n\geqslant g\geqslant 0$ we consider the moduli stack 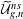 $\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ of curves
$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ of curves 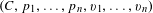 $(C,p_{1},\ldots ,p_{n},v_{1},\ldots ,v_{n})$ of arithmetic genus
$(C,p_{1},\ldots ,p_{n},v_{1},\ldots ,v_{n})$ of arithmetic genus  $g$ with
$g$ with  $n$ smooth marked points
$n$ smooth marked points 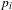 $p_{i}$ and nonzero tangent vectors
$p_{i}$ and nonzero tangent vectors 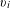 $v_{i}$ at them, such that the divisor
$v_{i}$ at them, such that the divisor 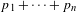 $p_{1}+\cdots +p_{n}$ is nonspecial (has
$p_{1}+\cdots +p_{n}$ is nonspecial (has 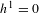 $h^{1}=0$) and ample. With some mild restrictions on the characteristic we show that it is a scheme, affine over the Grassmannian
$h^{1}=0$) and ample. With some mild restrictions on the characteristic we show that it is a scheme, affine over the Grassmannian 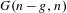 $G(n-g,n)$. We also construct an isomorphism of
$G(n-g,n)$. We also construct an isomorphism of 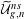 $\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ with a certain relative moduli of
$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ with a certain relative moduli of 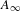 $A_{\infty }$-structures (up to an equivalence) over a family of graded associative algebras parametrized by
$A_{\infty }$-structures (up to an equivalence) over a family of graded associative algebras parametrized by 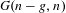 $G(n-g,n)$.
$G(n-g,n)$.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 6 , November 2019 , pp. 1295 - 1329
- Copyright
- © Cambridge University Press 2017
Footnotes
Supported in part by the NSF grant DMS-1400390 and by the Russian Academic Excellence Project ‘5-100’.
References
- 2
- Cited by

