Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-23T16:02:48.426Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MODULI SPACE OF TWISTED CANONICAL DIVISORS

Part of: Projective and enumerative geometry Curves

Published online by Cambridge University Press:  05 April 2016

Gavril Farkas  and
Rahul Pandharipande
Gavril Farkas
Affiliation:
Humboldt-Universität zu Berlin, Institut Für Mathematik, Unter den Linden 6, 10099 Berlin, Germany (farkas@math.hu-berlin.de)
Rahul Pandharipande
Affiliation:
ETH Zürich, Department of Mathematics, Raemistrasse 101, 8092 Zürich, Switzerland (rahul@math.ethz.ch)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

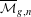The moduli space of canonical divisors (with prescribed zeros and poles) on nonsingular curves is not compact since the curve may degenerate. We define a proper moduli space of twisted canonical divisors in $\overline{{\mathcal{M}}}_{g,n}$ which includes the space of canonical divisors as an open subset. The theory leads to geometric/combinatorial constraints on the closures of the moduli spaces of canonical divisors.

In case the differentials have at least one pole (the strictly meromorphic case), the moduli spaces of twisted canonical divisors on genus $g$ curves are of pure codimension $g$ in 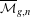$\overline{{\mathcal{M}}}_{g,n}$. In addition to the closure of the canonical divisors on nonsingular curves, the moduli spaces have virtual components. In the Appendix A, a complete proposal relating the sum of the fundamental classes of all components (with intrinsic multiplicities) to a formula of Pixton is proposed. The result is a precise and explicit conjecture in the tautological ring for the weighted fundamental class of the moduli spaces of twisted canonical divisors.

As a consequence of the conjecture, the classes of the closures of the moduli spaces of canonical divisors on nonsingular curves are determined (both in the holomorphic and meromorphic cases).

Keywords

holomorphic differentialsmoduli space of pointed curvestwisted canonical divisors

MSC classification

Primary: 14H10: Families, moduli (algebraic) 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 14N10: Enumerative problems (combinatorial problems)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 3 , June 2018 , pp. 615 - 672
Copyright
© Cambridge University Press 2016 

References

Bainbridge, M., Chen, D., Gendron, Q., Grushevsky, S. and Möller, M., in preparation.Google Scholar
Belorousski, P. and Pandharipande, R., A descendent relation in genus 2, Ann. Sc. Norm. Super. Pisa Cl. Sci. 29 (2000), 171–191.Google Scholar
Caporaso, L. and Sernesi, E., Recovering plane curves from their bitangents, J. Algebraic Geom. 12 (2003), 225–244.Google Scholar
Chen, D., Degenerations of abelian differentials, preprint, 2015, arXiv:1504.01983.Google Scholar
Chen, D. and Tarasca, N., Loci of curves with subcanonical points in low genus, preprint, arXiv:1501.02235.Google Scholar
Clader, E. and Janda, F., Pixton’s double ramification cycle relations, preprint, arXiv:1601.02871.Google Scholar
Cornalba, M., Moduli of curves and theta-characteristics, in Lectures on Riemann surfaces (Trieste, 1987), pp. 560–589 (World Scientific Publications, 1989).CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., The Kodaira dimension of the moduli space of curves of genus ⩾ 23, Invent. Math. 90 (1987), 359–387.Google Scholar
Eskin, A., Masur, H. and Zorich, A., Moduli spaces of abelian differentials: the principal boundary, counting problems and the Siegel-Veech constants, Publ. Math. Inst. Hautes Études Sci. 97 (2003), 61–179.Google Scholar
Eskin, A. and Okounkov, A., Asymptotics of the numbers of branched coverings of a torus and volumes of moduli spaces of holomorphic differential, Invent. Math. 145 (2001), 59–103.CrossRefGoogle Scholar
Faber, C. and Pandharipande, R., Relative maps and tautological classes, J. Eur. Math. Soc (JEMS) 7 (2005), 13–49.Google Scholar
Farkas, G., The birational type of the moduli space of even spin curves, Adv. Math. 223 (2010), 433–443.Google Scholar
Fulton, W., Intersection Theory (Springer, Berlin, 1984).Google Scholar
Gendron, Q., The Deligne–Mumford and the incidence variety compactifications of the strata of $\unicode[STIX]{x1D6FA}{\mathcal{M}}_{g}$ , preprint, arXiv:1503.03338.Google Scholar
Graber, T. and Pandharipande, R., Constructions of nontautological classes on moduli spaces of curves, Michigan Math. J. 51 (2003), 93–109.Google Scholar
Hain, R., Normal Functions and the Geometry of Moduli Spaces of Curves (ed. Farkas, G. and Morrison, I.), Handbook of Moduli, Volume I, pp. 527–578 (International Press, 2013).Google Scholar
Hilton, H., Plane Algebraic Curves (Clarendon, Oxford, 1920).Google Scholar
Janda, F., Pandharipande, R., Pixton, A. and Zvonkine, D., Double ramification cycles on the moduli spaces of curves, preprint, arXiv:1602.04705.Google Scholar
Janda, F., in preparation.Google Scholar
Kiem, Y.-H. and Li, J., Localizing virtual classes by cosections, J. Amer. Math. Soc. 26 (2013), 1025–1050.Google Scholar
Kontsevich, M. and Zorich, A., Connected components of the moduli spaces of abelian differentials with prescribed singularities, Invent. Math. 153 (2003), 631–678.Google Scholar
Masur, H., Interval exchange transformations and measured foliations, Ann. of Math. (2) 115 (1982), 169–200.Google Scholar
Pandharipande, R., Pixton, A. and Zvonkine, D., Relations on M g, n via 3-spin structures, J. Amer. Math. Soc. 28 (2015), 279–309.CrossRefGoogle Scholar
Pixton, A., Double ramification cycles and tautological relations on $\overline{{\mathcal{M}}}_{g,n}$ , preprint, 2014.Google Scholar
Polishchuk, A., Moduli spaces of curves with effective r-spin structures, in Gromov–Witten Theory of Spin Curves and Orbifolds, Contemporary Mathematics, Volume 403, p. 20 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Sauvaget, A. and Zvonkine, D., in preparation.Google Scholar
Veech, W. A., Moduli spaces of quadratic differentials, J. Anal. Math. 55 (1990), 117–171.Google Scholar
Wolpert, S., Infinitesimal deformations of nodal stable curves, Adv. Math. 244 (2013), 413–440.Google Scholar