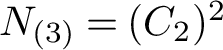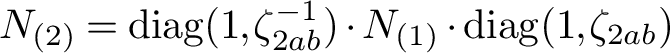1 Introduction
1.1 Lie Groups
Hopf proved that the cohomology of a real connected compact Lie group
![]() $\mathcal {G}$
is a free exterior algebra on
$\mathcal {G}$
is a free exterior algebra on
![]() $r=\mathrm {rank}(\mathcal {G})$
generators of odd degree [Reference Hopf12]. Its Poincaré series is therefore given by
$r=\mathrm {rank}(\mathcal {G})$
generators of odd degree [Reference Hopf12]. Its Poincaré series is therefore given by
 $$ \begin{align}\mathrm{Hilb}(H^*(\mathcal{G});q) = \prod_{i=1}^r (1+q^{2e_i+1}).\end{align} $$
$$ \begin{align}\mathrm{Hilb}(H^*(\mathcal{G});q) = \prod_{i=1}^r (1+q^{2e_i+1}).\end{align} $$
Chevalley presented these
![]() $e_i$
for the exceptional simple Lie algebras in his 1950 address at the International Congress of Mathematicians [Reference Chevalley8], and Coxeter recognised them from previous work with real reflection groups [Reference Coxeter10]. This observation has led to deep relationships between the cohomology of
$e_i$
for the exceptional simple Lie algebras in his 1950 address at the International Congress of Mathematicians [Reference Chevalley8], and Coxeter recognised them from previous work with real reflection groups [Reference Coxeter10]. This observation has led to deep relationships between the cohomology of
![]() $\mathcal {G}$
and the invariant theory of the corresponding Weyl group
$\mathcal {G}$
and the invariant theory of the corresponding Weyl group
![]() $W=N_{\mathcal {G}}(T)/T$
, where T is a maximal torus in
$W=N_{\mathcal {G}}(T)/T$
, where T is a maximal torus in
![]() $\mathcal {G}$
[Reference Reiner and Shepler18, Reference Reeder17] – notably,
$\mathcal {G}$
[Reference Reiner and Shepler18, Reference Reeder17] – notably,
 $$ \begin{align*}H^*(\mathcal{G}) \simeq \left(H^*(\mathcal{G}/T) \times H^*(T)\right)^W \simeq \left(S(V^*)/{I_W^+} \otimes \bigwedge V^*\right)^W\!\!\!\!\!,\end{align*} $$
$$ \begin{align*}H^*(\mathcal{G}) \simeq \left(H^*(\mathcal{G}/T) \times H^*(T)\right)^W \simeq \left(S(V^*)/{I_W^+} \otimes \bigwedge V^*\right)^W\!\!\!\!\!,\end{align*} $$
where
![]() $V=\mathrm {Lie}(T)$
is the reflection representation of W,
$V=\mathrm {Lie}(T)$
is the reflection representation of W,
![]() $S(V^*)$
is the algebra of polynomial functions on V and
$S(V^*)$
is the algebra of polynomial functions on V and
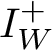 ${I_W^+}$
is the ideal generated by the W-invariant polynomials in
${I_W^+}$
is the ideal generated by the W-invariant polynomials in
![]() $S(V^*)$
with no constant term. For more details, we refer the reader to the wonderful survey [Reference Barcelo and Goupil3].
$S(V^*)$
with no constant term. For more details, we refer the reader to the wonderful survey [Reference Barcelo and Goupil3].
1.2 Complex Reflection Groups
It turns out that the
![]() $e_i$
in Equation (1) can be computed from the generating function for the dimension of the fixed space
$e_i$
in Equation (1) can be computed from the generating function for the dimension of the fixed space
![]() ${\mathrm {fix}}(w):=\dim (\ker (1-w))$
for
${\mathrm {fix}}(w):=\dim (\ker (1-w))$
for
![]() $w\in W$
, via the remarkable formula:
$w\in W$
, via the remarkable formula:
 $$ \begin{align}\sum_{w \in W} q^{{\mathrm{fix}}(w)} = \prod_{i=1}^r (q+e_i).\end{align} $$
$$ \begin{align}\sum_{w \in W} q^{{\mathrm{fix}}(w)} = \prod_{i=1}^r (q+e_i).\end{align} $$
Shephard and Todd verified case by case that the same sum still factors when W is replaced by a finite complex reflection group
![]() $G\subset \mathrm {GL}(V)$
acting by reflections on a complex vector space V of dimension r [Reference Shephard and Todd19, Theorem 5.3]. The
$G\subset \mathrm {GL}(V)$
acting by reflections on a complex vector space V of dimension r [Reference Shephard and Todd19, Theorem 5.3]. The
![]() $e_i$
are now determined by the degrees
$e_i$
are now determined by the degrees
![]() $d_i$
of the fundamental invariants of G on V as
$d_i$
of the fundamental invariants of G on V as
![]() $e_i=d_i-1$
. A case-free proof of this result was given by Solomon in [Reference Solomon20], mirroring Hopf’s result:
$e_i=d_i-1$
. A case-free proof of this result was given by Solomon in [Reference Solomon20], mirroring Hopf’s result:
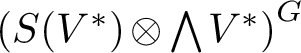 $\left (S(V^*) \otimes \bigwedge V^*\right )^G$
is a free exterior algebra over the ring
$\left (S(V^*) \otimes \bigwedge V^*\right )^G$
is a free exterior algebra over the ring
![]() $S(V^*)^G$
of G-invariant polynomials, which gives a factorisation of the Poincaré series of the G-invariant differential forms
$S(V^*)^G$
of G-invariant polynomials, which gives a factorisation of the Poincaré series of the G-invariant differential forms
 $$ \begin{align} \mathrm{Hilb}\left(\left(S(V^*) \otimes \bigwedge V^* \right)^G;q,u\right) = \prod_{i=1}^r \frac{1+u q^{e_i}}{1-q^{d_i}}. \end{align} $$
$$ \begin{align} \mathrm{Hilb}\left(\left(S(V^*) \otimes \bigwedge V^* \right)^G;q,u\right) = \prod_{i=1}^r \frac{1+u q^{e_i}}{1-q^{d_i}}. \end{align} $$
Computing the trace of the projection
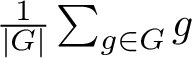 $\frac {1}{|G|}\sum _{g\in G} g$
to the subspace of G-invariants on
$\frac {1}{|G|}\sum _{g\in G} g$
to the subspace of G-invariants on
![]() $S(V^*) \otimes \bigwedge V^*$
, specialising to
$S(V^*) \otimes \bigwedge V^*$
, specialising to
![]() $u=q(1-x)-1$
and taking the limit as
$u=q(1-x)-1$
and taking the limit as
![]() $x \to 1$
gives the Shephard-Todd result in Equation (2).
$x \to 1$
gives the Shephard-Todd result in Equation (2).
1.3 Galois twists and cohomology
More generally, the fake degree of an m-dimensional simple G-module M is the polynomial encoding the degrees in which M occurs in the coinvariant algebra
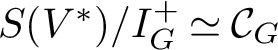 $S(V^*)/{I_G^+}\simeq {\mathcal {C}_G}$
:
$S(V^*)/{I_G^+}\simeq {\mathcal {C}_G}$
:
 $$ \begin{align}f_M(q)=\sum_{i} (({\mathcal{C}_G})_i,M)q^i =\sum_{i=1}^m q^{e_i(M)}.\end{align} $$
$$ \begin{align}f_M(q)=\sum_{i} (({\mathcal{C}_G})_i,M)q^i =\sum_{i=1}^m q^{e_i(M)}.\end{align} $$
The fake degree of a reducible G-module is defined as the sum of the fake degrees of its simple direct summands. The integers
![]() $e_i(M)$
in Equation (4) are called the M-exponents of G.
$e_i(M)$
in Equation (4) are called the M-exponents of G.
Letting
![]() $\zeta _G$
denote a primitive
$\zeta _G$
denote a primitive
![]() $|G|$
th root of unity, for
$|G|$
th root of unity, for
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
the Galois twist
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
the Galois twist
![]() $V^\sigma $
is the representation of G obtained by applying
$V^\sigma $
is the representation of G obtained by applying
![]() $\sigma $
to its matrix entries. In [Reference Orlik and Solomon16], Orlik and Solomon gave a beautiful generalisation of Equations (2) and (3) that takes into account these Galois twists (see Section 2.3).
$\sigma $
to its matrix entries. In [Reference Orlik and Solomon16], Orlik and Solomon gave a beautiful generalisation of Equations (2) and (3) that takes into account these Galois twists (see Section 2.3).
Theorem 1.1 [Reference Orlik and Solomon16, Thm. 3.3]
Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then
 $$ \begin{align*}\sum_{g \in G} \left(\prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_{V} (g)} = \prod_{i=1}^r \left(q+e_i(V^\sigma) \right),\end{align*} $$
$$ \begin{align*}\sum_{g \in G} \left(\prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_{V} (g)} = \prod_{i=1}^r \left(q+e_i(V^\sigma) \right),\end{align*} $$
where the
![]() $\lambda _i(g)$
are the eigenvalues of
$\lambda _i(g)$
are the eigenvalues of
![]() $g \in G$
acting on V.
$g \in G$
acting on V.
When
![]() $\sigma :\zeta _G\mapsto \overline {\zeta _G}$
is complex conjugation, Orlik and Solomon [Reference Orlik and Solomon16, Thm. 4.8] further connected their Theorem 1.1 to the cohomology of the complement of the corresponding hyperplane arrangement – in this case
$\sigma :\zeta _G\mapsto \overline {\zeta _G}$
is complex conjugation, Orlik and Solomon [Reference Orlik and Solomon16, Thm. 4.8] further connected their Theorem 1.1 to the cohomology of the complement of the corresponding hyperplane arrangement – in this case
![]() $V^\sigma \simeq V^*$
as a G-representation, and the co-exponents
$V^\sigma \simeq V^*$
as a G-representation, and the co-exponents
![]() $e_i(V^*)$
are the degrees of the generators of the cohomology ring of the complement of the hyperplane arrangement.
$e_i(V^*)$
are the degrees of the generators of the cohomology ring of the complement of the hyperplane arrangement.
1.4 Normal Reflection Subgroups of Complex Reflection Groups
Let
![]() $G \subset \mathrm {GL}(V)$
be a complex reflection group. We say that
$G \subset \mathrm {GL}(V)$
be a complex reflection group. We say that
![]() $N \trianglelefteq G$
is a normal reflection subgroup of G if it is a normal subgroup of G that is generated by reflections. The main theorem of this article, Theorem 1.4, gives a new refinement of Theorem 1.1 to accommodate a normal reflection subgroup. The following result is a special case of [Reference Bessis, Bonnafé and Rouquier4], where they consider the more general notion of bon sous-groupe distingué in lieu of our normal reflection subgroup N of G.
$N \trianglelefteq G$
is a normal reflection subgroup of G if it is a normal subgroup of G that is generated by reflections. The main theorem of this article, Theorem 1.4, gives a new refinement of Theorem 1.1 to accommodate a normal reflection subgroup. The following result is a special case of [Reference Bessis, Bonnafé and Rouquier4], where they consider the more general notion of bon sous-groupe distingué in lieu of our normal reflection subgroup N of G.
Theorem 1.2. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Then
$N\trianglelefteq G$
be a normal reflection subgroup. Then
![]() $G/N=H$
acts as a reflection group on the vector space
$G/N=H$
acts as a reflection group on the vector space
![]() ${V/N={E}}$
.
${V/N={E}}$
.
The bons sous-groupes distingués of [Reference Bessis, Bonnafé and Rouquier4] are precisely those normal subgroups for which the associated quotient group is a reflection group acting on the tangent space at
![]() $0$
of
$0$
of
![]() $V/N$
, which is a strictly weaker condition than being a normal reflection subgroup. Our proof of Theorem 1.2 in Section 3 follows the ideas of [Reference Bessis, Bonnafé and Rouquier4] but specialised to our more restricted setting where the normal subgroup under consideration is actually a normal reflection subgroup. In this more restricted setting, we are able to prove the new results Theorems 1.3 and 1.4 stated below.
$V/N$
, which is a strictly weaker condition than being a normal reflection subgroup. Our proof of Theorem 1.2 in Section 3 follows the ideas of [Reference Bessis, Bonnafé and Rouquier4] but specialised to our more restricted setting where the normal subgroup under consideration is actually a normal reflection subgroup. In this more restricted setting, we are able to prove the new results Theorems 1.3 and 1.4 stated below.
The technical definition of the G-module
![]() ${U^N_\sigma }$
that mediates the statement of the following result is given in Definition 2.9. Because we are dealing with multiple reflection groups acting on multiple spaces, we will begin labelling exponents and degrees by their corresponding groups.
${U^N_\sigma }$
that mediates the statement of the following result is given in Definition 2.9. Because we are dealing with multiple reflection groups acting on multiple spaces, we will begin labelling exponents and degrees by their corresponding groups.
Theorem 1.3. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Let
$N\trianglelefteq G$
be a normal reflection subgroup. Let
![]() $H=G/N$
and
$H=G/N$
and
![]() ${E}=V/N$
. Then for a suitable choice of indexing we have
${E}=V/N$
. Then for a suitable choice of indexing we have
 $$ \begin{align*} e_i^N({V^\sigma}) {+} e_i^G({U^N_\sigma}) & = e_i^G({V^\sigma})\\ d_i^N \cdot e_i^H({E^\sigma}) & = e_i^G({E^\sigma})\\ d_i^N\cdot d_i^H & =d_i^G. \end{align*} $$
$$ \begin{align*} e_i^N({V^\sigma}) {+} e_i^G({U^N_\sigma}) & = e_i^G({V^\sigma})\\ d_i^N \cdot e_i^H({E^\sigma}) & = e_i^G({E^\sigma})\\ d_i^N\cdot d_i^H & =d_i^G. \end{align*} $$
In the special case
![]() $\sigma =1$
, it is well known that
$\sigma =1$
, it is well known that
![]() ${U^N_\sigma }\simeq {E}$
as G-modules (see Definition 2.9 and Lemma 4.1), so that Theorem 1.3 coincides with [Reference Arreche and Williams1, Theorem 1.3] in this case. As we explain in Remark 4.2, in this special case where
${U^N_\sigma }\simeq {E}$
as G-modules (see Definition 2.9 and Lemma 4.1), so that Theorem 1.3 coincides with [Reference Arreche and Williams1, Theorem 1.3] in this case. As we explain in Remark 4.2, in this special case where
![]() $\sigma =1$
, the equalities in Theorem 1.3 are compatible with the relations
$\sigma =1$
, the equalities in Theorem 1.3 are compatible with the relations
![]() $d_i=e_i+1$
between classical exponents and degrees for the three reflection groups involved.
$d_i=e_i+1$
between classical exponents and degrees for the three reflection groups involved.
An essential tool in our proof of Theorem 1.3 is Proposition 3.3, which gives a graded G-module isomorphism
![]() ${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
relating the spaces of harmonic polynomials for N and H to that for G, which is an interesting and useful result in its own right.
${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
relating the spaces of harmonic polynomials for N and H to that for G, which is an interesting and useful result in its own right.
Our Theorem 1.4 generalises the Orlik-Solomon formula from Theorem 1.1 to take into account the additional combinatorial data arising from a normal reflection subgroup. The technical definition of the G-module
![]() ${U^N_\sigma }$
is again given in Definition 2.9.
${U^N_\sigma }$
is again given in Definition 2.9.
Theorem 1.4. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Let
$N\trianglelefteq G$
be a normal reflection subgroup. Let
![]() ${E}=V/N$
and
${E}=V/N$
and
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then for a suitable choice of indexing we have
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then for a suitable choice of indexing we have
 $$ \begin{align*}\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)} = \prod_{i=1}^r \left(qt+e_i^N(V^\sigma) t + e_i^G({U^N_\sigma})\right),\end{align*} $$
$$ \begin{align*}\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)} = \prod_{i=1}^r \left(qt+e_i^N(V^\sigma) t + e_i^G({U^N_\sigma})\right),\end{align*} $$
where the
![]() $\lambda _i(g)$
are the eigenvalues of
$\lambda _i(g)$
are the eigenvalues of
![]() $g\in G$
acting on V.
$g\in G$
acting on V.
In view of Theorem 1.3, specialising to
![]() $t=1$
recovers Theorem 1.1. Moreover, because
$t=1$
recovers Theorem 1.1. Moreover, because
![]() ${U^N_\sigma }\simeq {E}$
as G-modules when
${U^N_\sigma }\simeq {E}$
as G-modules when
![]() $\sigma =1$
(see again Definition 2.9 and Lemma 4.1), Theorem 1.4 coincides with [Reference Arreche and Williams1, Theorem 1.5] in this case, which when similarly specialised to
$\sigma =1$
(see again Definition 2.9 and Lemma 4.1), Theorem 1.4 coincides with [Reference Arreche and Williams1, Theorem 1.5] in this case, which when similarly specialised to
![]() $t=1$
recovers Equation (2). As explained in Remark 4.12, one can also recover Theorem 1.1 for the reflection group N from Theorem 1.4 by applying
$t=1$
recovers Equation (2). As explained in Remark 4.12, one can also recover Theorem 1.1 for the reflection group N from Theorem 1.4 by applying
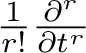 $\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
on both sides. In the special case
$\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
on both sides. In the special case
![]() $\sigma =1$
, one can recover Equation (2) for the reflection group H by specialising Theorem 1.4 to
$\sigma =1$
, one can recover Equation (2) for the reflection group H by specialising Theorem 1.4 to
![]() $q=1$
and dividing by
$q=1$
and dividing by
![]() $|N|$
on both sides, but this same specialisation does not seem to be directly related to Theorem 1.1 for H in general for arbitrary
$|N|$
on both sides, but this same specialisation does not seem to be directly related to Theorem 1.1 for H in general for arbitrary
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
.
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
.
Our proof of Theorem 1.4 follows a strategy similar to the one employed in [Reference Orlik and Solomon16]: we compute the Poincaré series for
![]() $(S(V^*)\otimes \bigwedge {(U^N_\sigma )^*})^G$
in two equivalent and standard ways and then obtain Theorem 1.4 from a well-chosen specialisation. However, a delicate technical issue arises in that our specialisation does not provide the correct contribution term by term in the left-hand side of Theorem 1.4. We overcome this technical difficulty by applying the results of [Reference Bonnafé, Lehrer and Michel7], where the authors develop a ‘twisted invariant theory’ for cosets
$(S(V^*)\otimes \bigwedge {(U^N_\sigma )^*})^G$
in two equivalent and standard ways and then obtain Theorem 1.4 from a well-chosen specialisation. However, a delicate technical issue arises in that our specialisation does not provide the correct contribution term by term in the left-hand side of Theorem 1.4. We overcome this technical difficulty by applying the results of [Reference Bonnafé, Lehrer and Michel7], where the authors develop a ‘twisted invariant theory’ for cosets
![]() $Ng$
of a reflection group
$Ng$
of a reflection group
![]() $N\subset \mathrm {GL}(V)$
for
$N\subset \mathrm {GL}(V)$
for
![]() $g\in \mathrm {GL}(V)$
an element of the normaliser of N in
$g\in \mathrm {GL}(V)$
an element of the normaliser of N in
![]() $\mathrm {GL}(V)$
. Our proof of Theorem 1.4 applies the results of [Reference Bonnafé, Lehrer and Michel7] to the special situation where the cosets
$\mathrm {GL}(V)$
. Our proof of Theorem 1.4 applies the results of [Reference Bonnafé, Lehrer and Michel7] to the special situation where the cosets
![]() $Ng$
all come from
$Ng$
all come from
![]() $g\in G$
, a reflection group containing N as a normal reflection subgroup, to show that our specialisation argument does provide the correct contribution coset by coset.
$g\in G$
, a reflection group containing N as a normal reflection subgroup, to show that our specialisation argument does provide the correct contribution coset by coset.
In summary, we have applied results and insights from [Reference Bonnafé, Lehrer and Michel7, Reference Bessis, Bonnafé and Rouquier4] in the development of new results in the invariant theory for complex reflection groups G taking into account the additional combinatorial data arising from normal reflection subgroups
![]() $N\trianglelefteq G $
and their corresponding reflection group quotients
$N\trianglelefteq G $
and their corresponding reflection group quotients
![]() $H=G/N$
. The setting of [Reference Bessis, Bonnafé and Rouquier4] considers more general N (their bons sous-groups distingués), whereas the setting of [Reference Bonnafé, Lehrer and Michel7] considers more general cosets
$H=G/N$
. The setting of [Reference Bessis, Bonnafé and Rouquier4] considers more general N (their bons sous-groups distingués), whereas the setting of [Reference Bonnafé, Lehrer and Michel7] considers more general cosets
![]() $Ng$
(for arbitrary g in the normaliser of N). The general study of normal reflection subgroups initiated in this article is both natural, because it lies in the intersection [Reference Bessis, Bonnafé and Rouquier4]
$Ng$
(for arbitrary g in the normaliser of N). The general study of normal reflection subgroups initiated in this article is both natural, because it lies in the intersection [Reference Bessis, Bonnafé and Rouquier4]
![]() $\cap $
[Reference Bonnafé, Lehrer and Michel7], as well as productive, as evidenced, for example, by Theorems 1.3 and 1.4, the graded G-module isomorphism
$\cap $
[Reference Bonnafé, Lehrer and Michel7], as well as productive, as evidenced, for example, by Theorems 1.3 and 1.4, the graded G-module isomorphism
![]() ${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
of Proposition 3.3 and the ancillary results in Section 3 relating the amenability of different modules with respect to the groups G, N, and H.
${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
of Proposition 3.3 and the ancillary results in Section 3 relating the amenability of different modules with respect to the groups G, N, and H.
1.5 Organisation
We recall standard results about complex reflection groups in Section 2. In Section 3, we introduce normal reflection subgroups and prove ancillary results, relating spaces of harmonic polynomials and amenability with respect to different reflection groups. We prove the main results stated in the Introduction, Theorems 1.3 and 1.4, in Section 4. In Section 5 we recall the case-by-case results of [Reference Williams22] and discuss how they are obtained in a case-free manner by the methods of the present article. In Section 6 we provide a complete classification of the normal reflection subgroups of the irreducible complex reflection groups. Finally, in Section 7 we give several examples that illustrate our general results.
2 Invariant Theory of Reflection Groups
Let V be a complex vector space of dimension r. A reflection is an element of
![]() $\mathrm {GL}(V)$
of finite order that fixes some hyperplane pointwise. A complex reflection group G is a finite subgroup of
$\mathrm {GL}(V)$
of finite order that fixes some hyperplane pointwise. A complex reflection group G is a finite subgroup of
![]() $\mathrm {GL}(V)$
that is generated by reflections. A complex reflection group G is called irreducible if V is a simple G-module; V is then called the reflection representation of G. A (normal) reflection subgroup of G is a (normal) subgroup that is generated by reflections. In what follows, a G-module will always be a complex representation of G.
$\mathrm {GL}(V)$
that is generated by reflections. A complex reflection group G is called irreducible if V is a simple G-module; V is then called the reflection representation of G. A (normal) reflection subgroup of G is a (normal) subgroup that is generated by reflections. In what follows, a G-module will always be a complex representation of G.
2.1 Chevalley-Shephard-Todd’s Theorem
Let
![]() $S(V^*)$
be the symmetric algebra on the dual vector space
$S(V^*)$
be the symmetric algebra on the dual vector space
![]() $V^*$
, and write
$V^*$
, and write
![]() $S(V^*)^G$
for its G-invariant subring. By a classical theorem of Shephard-Todd [Reference Shephard and Todd19] and Chevalley [Reference Chevalley9], a finite subgroup
$S(V^*)^G$
for its G-invariant subring. By a classical theorem of Shephard-Todd [Reference Shephard and Todd19] and Chevalley [Reference Chevalley9], a finite subgroup
![]() $G \subset \mathrm {GL}(V)$
is a complex reflection group if and only if
$G \subset \mathrm {GL}(V)$
is a complex reflection group if and only if
![]() $S(V^*)^G$
is a polynomial ring, and in this case
$S(V^*)^G$
is a polynomial ring, and in this case
![]() $S(V^*)^G$
is generated by r algebraically independent homogeneous polynomials – the degrees
$S(V^*)^G$
is generated by r algebraically independent homogeneous polynomials – the degrees
![]() $d_1\leq \cdots \leq d_r$
of these polynomials are invariants of G.
$d_1\leq \cdots \leq d_r$
of these polynomials are invariants of G.
Theorem 2.1 [Reference Chevalley9, Reference Shephard and Todd19]
A finite subgroup
![]() $G \subset \mathrm {GL}(V)$
is a complex reflection group if and only if there exist
$G \subset \mathrm {GL}(V)$
is a complex reflection group if and only if there exist
![]() $r=\mathrm {dim}(V)$
homogeneous algebraically independent polynomials
$r=\mathrm {dim}(V)$
homogeneous algebraically independent polynomials
![]() ${G}_1,\ldots ,{G}_r$
such that
${G}_1,\ldots ,{G}_r$
such that
![]() $S(V^*)^G=\mathbb {C}[{G}_1,\ldots ,{G}_r]$
. In this case,
$S(V^*)^G=\mathbb {C}[{G}_1,\ldots ,{G}_r]$
. In this case,
![]() $|G|=\prod _{i=1}^r d_i$
, where
$|G|=\prod _{i=1}^r d_i$
, where
![]() $d_i=\mathrm {deg}({G}_i)$
.
$d_i=\mathrm {deg}({G}_i)$
.
Let
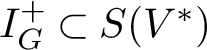 ${I_G^+}\subset S(V^*)$
denote the ideal generated by homogeneous G-invariant polynomials of positive degree. In [Reference Chevalley9], Chevalley proved that, as an ungraded G-module,
${I_G^+}\subset S(V^*)$
denote the ideal generated by homogeneous G-invariant polynomials of positive degree. In [Reference Chevalley9], Chevalley proved that, as an ungraded G-module,
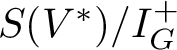 $S(V^*)/{I_G^+}$
affords the regular representation of G. Because
$S(V^*)/{I_G^+}$
affords the regular representation of G. Because
![]() ${I_G^+}$
is G-stable, we may choose a G-stable complement
${I_G^+}$
is G-stable, we may choose a G-stable complement
![]() ${\mathcal {C}_G}\subset S(V^*)$
, so that
${\mathcal {C}_G}\subset S(V^*)$
, so that
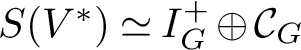 $S(V^*)\simeq {I_G^+}\oplus {\mathcal {C}_G}$
as graded G-modules, and
$S(V^*)\simeq {I_G^+}\oplus {\mathcal {C}_G}$
as graded G-modules, and
![]() ${\mathcal {C}_G}$
is a graded version of the regular representation of G. Chevalley also proved in [Reference Chevalley9] that
${\mathcal {C}_G}$
is a graded version of the regular representation of G. Chevalley also proved in [Reference Chevalley9] that
![]() $S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_G}$
as graded G-modules. A canonical choice for such a G-stable complement
$S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_G}$
as graded G-modules. A canonical choice for such a G-stable complement
![]() ${\mathcal {C}_G}$
is the space of G-harmonic polynomials [Reference Lehrer and Taylor14, Corollary 9.37]; that is, polynomials in
${\mathcal {C}_G}$
is the space of G-harmonic polynomials [Reference Lehrer and Taylor14, Corollary 9.37]; that is, polynomials in
![]() $S(V^*)$
that are annihilated by all G-invariant polynomial differential operators with no constant term [Reference Lehrer and Taylor14, Definition 9.35].
$S(V^*)$
that are annihilated by all G-invariant polynomial differential operators with no constant term [Reference Lehrer and Taylor14, Definition 9.35].
Remark 2.2. The space
![]() ${\mathcal {C}_G}$
of G-harmonic polynomials is stabilised by the normaliser of G in
${\mathcal {C}_G}$
of G-harmonic polynomials is stabilised by the normaliser of G in
![]() $\mathrm {GL}(V)$
[Reference Lehrer and Taylor14, Proposition 12.2]. This fact will be essential in our treatment of normal reflection subgroups.
$\mathrm {GL}(V)$
[Reference Lehrer and Taylor14, Proposition 12.2]. This fact will be essential in our treatment of normal reflection subgroups.
Our choice of notation
![]() $\mathcal {C}$
for the space of harmonic polynomials, instead of the more common and natural
$\mathcal {C}$
for the space of harmonic polynomials, instead of the more common and natural
![]() $\mathcal {H}$
used in the literature, is meant to avoid unfortunate phonetic confusion with the quotient group
$\mathcal {H}$
used in the literature, is meant to avoid unfortunate phonetic confusion with the quotient group
![]() $H=G/N$
that will play a prominent role in the rest of the article.
$H=G/N$
that will play a prominent role in the rest of the article.
2.2 Solomon’s Theorem
We recall the following celebrated theorem of Solomon.
Theorem 2.3 [Reference Solomon20]
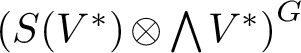 $\left (S(V^*)\otimes \bigwedge V^*\right )^G$
is a free exterior algebra over the ring of G-invariant polynomials
$\left (S(V^*)\otimes \bigwedge V^*\right )^G$
is a free exterior algebra over the ring of G-invariant polynomials
 $$ \begin{align*}\left(S(V^*)\otimes \bigwedge V^*\right)^G \simeq S(V^*)^G \otimes \bigwedge {(U^G)^*},\end{align*} $$
$$ \begin{align*}\left(S(V^*)\otimes \bigwedge V^*\right)^G \simeq S(V^*)^G \otimes \bigwedge {(U^G)^*},\end{align*} $$
where
![]() ${(U^G)^*}={\mathrm {span}}_{\mathbb {C}}\left \{d{G}_1,\ldots ,d{G}_r\right \}$
and
${(U^G)^*}={\mathrm {span}}_{\mathbb {C}}\left \{d{G}_1,\ldots ,d{G}_r\right \}$
and
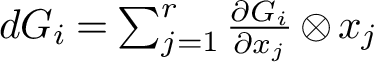 $d{G}_i=\sum _{j=1}^r \frac {\partial {G}_i}{\partial x_j} \otimes x_j$
form a free basis for
$d{G}_i=\sum _{j=1}^r \frac {\partial {G}_i}{\partial x_j} \otimes x_j$
form a free basis for
![]() $(S(V^*)\otimes V^*)^G$
over
$(S(V^*)\otimes V^*)^G$
over
![]() $S(V^*)^G$
.
$S(V^*)^G$
.
Computing the trace on
![]() $S(V^*) \otimes \bigwedge V^*$
of the projection to the G-invariants
$S(V^*) \otimes \bigwedge V^*$
of the projection to the G-invariants
 $\frac {1}{|G|}\sum _{g\in G} g$
gives a formula for the Poincaré series as a sum over the group.
$\frac {1}{|G|}\sum _{g\in G} g$
gives a formula for the Poincaré series as a sum over the group.
Corollary 2.4 [Reference Solomon20]
 $$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge V^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_V)}{\det(1-x g|_V)} = \prod_{i=1}^r\frac{1+x^{e_i^G(V)}u}{1-x_i^{d_i^G}}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge V^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_V)}{\det(1-x g|_V)} = \prod_{i=1}^r\frac{1+x^{e_i^G(V)}u}{1-x_i^{d_i^G}}.\end{align*} $$
Specialising Corollary 2.4 to
![]() $u=q(1-x)-1$
and taking the limit as
$u=q(1-x)-1$
and taking the limit as
![]() $x \to 1$
gives the Shephard-Todd formula from Equation (2).
$x \to 1$
gives the Shephard-Todd formula from Equation (2).
2.3 Orlik-Solomon’s Theorem
The reflection representation V of
![]() $G\subset \mathrm {GL}(V)$
can be realised over
$G\subset \mathrm {GL}(V)$
can be realised over
![]() $\mathbb{Q}(\zeta _{G})$
, where
$\mathbb{Q}(\zeta _{G})$
, where
![]() $\zeta _{G}$
denotes a primitive
$\zeta _{G}$
denotes a primitive
![]() $|G|$
th root of unity, in the sense that there is a choice of basis for V with respect to which
$|G|$
th root of unity, in the sense that there is a choice of basis for V with respect to which
![]() $G\subset \mathrm {GL}_r(\mathbb {Q}(\zeta _G))$
. For
$G\subset \mathrm {GL}_r(\mathbb {Q}(\zeta _G))$
. For
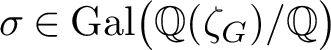 $\sigma \in \mathrm {Gal}\bigl (\mathbb {Q}(\zeta _{G})/\mathbb {Q}\bigr )$
, the Galois twist
$\sigma \in \mathrm {Gal}\bigl (\mathbb {Q}(\zeta _{G})/\mathbb {Q}\bigr )$
, the Galois twist
![]() $V^\sigma $
of V is the representation of G on the same underlying vector space V obtained by applying
$V^\sigma $
of V is the representation of G on the same underlying vector space V obtained by applying
![]() $\sigma $
to the matrix entries of
$\sigma $
to the matrix entries of
![]() $g\in \mathrm {GL}_r(\mathbb {Q}(\zeta _{G}))$
. Alternatively and equivalently, one can define
$g\in \mathrm {GL}_r(\mathbb {Q}(\zeta _{G}))$
. Alternatively and equivalently, one can define
![]() $V^\sigma $
by applying
$V^\sigma $
by applying
![]() $\tilde {\sigma }$
to the matrix entries of g in terms of any basis of V, for
$\tilde {\sigma }$
to the matrix entries of g in terms of any basis of V, for
![]() $\tilde {\sigma }$
any extension of
$\tilde {\sigma }$
any extension of
![]() $\sigma $
to a field automorphism of
$\sigma $
to a field automorphism of
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
In [Reference Orlik and Solomon16], Orlik and Solomon gave the following generalisation of Theorem 2.3.
Theorem 2.5 [Reference Orlik and Solomon16, Corollary 3.2]
 $$ \begin{align*}\left(S(V^*)\otimes \bigwedge (V^\sigma)^*\right)^G\simeq S(V^*)^G\otimes\bigwedge {(U^G_\sigma)^*},\end{align*} $$
$$ \begin{align*}\left(S(V^*)\otimes \bigwedge (V^\sigma)^*\right)^G\simeq S(V^*)^G\otimes\bigwedge {(U^G_\sigma)^*},\end{align*} $$
where the degrees of the homogeneous generators of
![]() ${(U^G_\sigma )^*}:=({\mathcal {C}_G}\otimes {(V^\sigma )^*})^G$
are
${(U^G_\sigma )^*}:=({\mathcal {C}_G}\otimes {(V^\sigma )^*})^G$
are
![]() $e_i^G({V^\sigma })$
, the
$e_i^G({V^\sigma })$
, the
![]() ${V^\sigma }$
-exponents of G.
${V^\sigma }$
-exponents of G.
Computing the Poincaré series in two ways as in Corollary 2.4 gives the following formula.
Corollary 2.6 [Reference Orlik and Solomon16, Theorem 3.3]
 $$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge (V^\sigma)^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_{V^\sigma})}{\det(1-x g|_V)} = \prod_{i=1}^r\frac{1+x^{e_i^G(V^\sigma)}u}{1-x_i^{d_i^G}}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge (V^\sigma)^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_{V^\sigma})}{\det(1-x g|_V)} = \prod_{i=1}^r\frac{1+x^{e_i^G(V^\sigma)}u}{1-x_i^{d_i^G}}.\end{align*} $$
Specialising Corollary 2.6 to
![]() $u=q(1-x)-1$
and taking the limit as
$u=q(1-x)-1$
and taking the limit as
![]() $x \to 1$
gives Theorem 1.1.
$x \to 1$
gives Theorem 1.1.
2.4 Amenable Representations
More generally, an m-dimensional G-module M satisfying
![]() $\sum _{i=1}^m e_i^G(M) = e^G_1(\bigwedge ^m M)$
is called amenable. This amenability condition can be shown to be equivalent to the requirement that
$\sum _{i=1}^m e_i^G(M) = e^G_1(\bigwedge ^m M)$
is called amenable. This amenability condition can be shown to be equivalent to the requirement that
![]() $(S(V^*)\otimes \bigwedge M^*)^G$
be a free exterior algebra over
$(S(V^*)\otimes \bigwedge M^*)^G$
be a free exterior algebra over
![]() $S(V^*)^G$
. Because, in particular, Galois twists
$S(V^*)^G$
. Because, in particular, Galois twists
![]() $V^\sigma $
of the reflection representation V of G are amenable, the following theorem generalises Theorem 2.5.
$V^\sigma $
of the reflection representation V of G are amenable, the following theorem generalises Theorem 2.5.
Theorem 2.7 [Reference Orlik and Solomon16, Theorem 3.1]
Let M be an amenable G-module. Then
 $$ \begin{align*}\left(S(V^*)\otimes \bigwedge M^*\right)^G\simeq S(V^*)^G\otimes\bigwedge {(U_M^G)^*},\end{align*} $$
$$ \begin{align*}\left(S(V^*)\otimes \bigwedge M^*\right)^G\simeq S(V^*)^G\otimes\bigwedge {(U_M^G)^*},\end{align*} $$
where
![]() ${(U_M^G)^*}:=({\mathcal {C}_G}\otimes M^*)^G$
and the degrees of the homogeneous generators of
${(U_M^G)^*}:=({\mathcal {C}_G}\otimes M^*)^G$
and the degrees of the homogeneous generators of
![]() ${(U_M^G)^*}$
are
${(U_M^G)^*}$
are
![]() $e_i^G(M)$
, the M-exponents of G.
$e_i^G(M)$
, the M-exponents of G.
From this, one can pursue the usual strategy of computing the Poincaré series of
![]() $(S(V^*)\otimes \bigwedge M^*)^G$
in two different ways to obtain the following.
$(S(V^*)\otimes \bigwedge M^*)^G$
in two different ways to obtain the following.
Corollary 2.8. If M is an amenable G-module, then
 $$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge M^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_{M})}{\det(1-x g|_V)} = \frac{\prod_{i=1}^m (1+x^{e_i^G(M)}u)}{\prod_{i=1}^r (1-x_i^{d_i^G})}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}\left(\left(S(V^*)\otimes \bigwedge M^* \right)^G;x,u\right) = \frac{1}{|G|} \sum_{g \in G} \frac{\mathrm{det}(1+ug |_{M})}{\det(1-x g|_V)} = \frac{\prod_{i=1}^m (1+x^{e_i^G(M)}u)}{\prod_{i=1}^r (1-x_i^{d_i^G})}.\end{align*} $$
However, it is no longer clear how to specialise Corollary 2.8 in the same way as Corollaries 2.4 and 2.6 to obtain an analogue of Equation (2) and Theorem 1.1 in this generality.
Definition 2.9. Let M be a G-module. We define the Orlik-Solomon space
![]() ${U_M^G}$
to be the dual G-module to
${U_M^G}$
to be the dual G-module to
![]() ${(U_M^G)^*}:=({\mathcal {C}_G}\otimes M^*)^G$
. In the special case where
${(U_M^G)^*}:=({\mathcal {C}_G}\otimes M^*)^G$
. In the special case where
![]() $M=V$
, we write
$M=V$
, we write
![]() ${U^G}:=U_V^G$
. When
${U^G}:=U_V^G$
. When
![]() $M=V^\sigma $
, we write
$M=V^\sigma $
, we write
![]() ${U^G_\sigma }:=U_{V^\sigma }^G$
.
${U^G_\sigma }:=U_{V^\sigma }^G$
.
3 Normal Reflection Subgroups
The following theorem is a special case of results in [Reference Bessis, Bonnafé and Rouquier4] (where they consider the more general notion of bon sous-groupe distingué in lieu of our normal reflection subgroup N of G). We emphasise that our proof follows the ideas in [Reference Bessis, Bonnafé and Rouquier4], specialised to our more restricted setting.
Theorem 1.2. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Then
$N\trianglelefteq G$
be a normal reflection subgroup. Then
![]() $G/N=H$
acts as a reflection group on the vector space
$G/N=H$
acts as a reflection group on the vector space
![]() ${V/N={E}}$
.
${V/N={E}}$
.
Proof. We claim that there exist homogeneous generators
![]() ${N}_1,\dots ,{N}_r$
of
${N}_1,\dots ,{N}_r$
of
![]() $S(V^*)^N$
such that
$S(V^*)^N$
such that
![]() ${E}^*=\mathrm {span}_{\mathbb {C}}\{{N}_1,\ldots ,{N}_r\}$
is H-stable. By Theorem 2.1, the ring of N-invariants
${E}^*=\mathrm {span}_{\mathbb {C}}\{{N}_1,\ldots ,{N}_r\}$
is H-stable. By Theorem 2.1, the ring of N-invariants
![]() $S(V^*)^N=\mathbb {C}[\tilde {{N}}_1,\dots ,\tilde {{N}}_r]$
for some homogeneous algebraically independent
$S(V^*)^N=\mathbb {C}[\tilde {{N}}_1,\dots ,\tilde {{N}}_r]$
for some homogeneous algebraically independent
![]() $\tilde {{N}}_i$
. Let
$\tilde {{N}}_i$
. Let
![]() $I_+\subset S(V^*)^N$
be the ideal generated by homogeneous N-invariants of positive degree. Then both
$I_+\subset S(V^*)^N$
be the ideal generated by homogeneous N-invariants of positive degree. Then both
![]() $I_+$
and
$I_+$
and
![]() $I_+^2$
are H-stable homogeneous ideals, and therefore the algebraic tangent space
$I_+^2$
are H-stable homogeneous ideals, and therefore the algebraic tangent space
![]() $I_+/I_+^2$
to
$I_+/I_+^2$
to
![]() ${E}=V/N$
at
${E}=V/N$
at
![]() $0$
inherits a graded action of H that is compatible with the (graded) quotient map
$0$
inherits a graded action of H that is compatible with the (graded) quotient map
![]() $\pi :I_+\twoheadrightarrow I_+/I_+^2$
. Hence, there exists a graded H-equivariant section
$\pi :I_+\twoheadrightarrow I_+/I_+^2$
. Hence, there exists a graded H-equivariant section
![]() $\varphi :I_+/I_+^2\rightarrow I_+$
. Letting
$\varphi :I_+/I_+^2\rightarrow I_+$
. Letting
![]() ${N}_i=\varphi \circ \pi (\tilde {{N}}_i)$
, we see that
${N}_i=\varphi \circ \pi (\tilde {{N}}_i)$
, we see that
![]() ${N}_1,\dots ,{N}_r$
are still homogeneous algebraically independent generators for
${N}_1,\dots ,{N}_r$
are still homogeneous algebraically independent generators for
![]() $S(V^*)^N$
with
$S(V^*)^N$
with
![]() $\mathrm {deg}({N}_i)=\mathrm {deg}(\tilde {{N}}_i)$
and
$\mathrm {deg}({N}_i)=\mathrm {deg}(\tilde {{N}}_i)$
and
![]() ${E}^*:={\mathrm {span}}_{\mathbb {C}}\{{N}_1,\dots ,{N}_r\}$
is H-stable.
${E}^*:={\mathrm {span}}_{\mathbb {C}}\{{N}_1,\dots ,{N}_r\}$
is H-stable.
Let
![]() $\mathbf {x}=\{x_1,\dots ,x_r\}$
denote a dual basis for V and
$\mathbf {x}=\{x_1,\dots ,x_r\}$
denote a dual basis for V and
![]() $\mathbf {{N}}=\{{N}_1,\dots ,{N}_r\}$
denote an H-stable basis for
$\mathbf {{N}}=\{{N}_1,\dots ,{N}_r\}$
denote an H-stable basis for
![]() ${E^*}$
as above. Because the action of H on the polynomial ring
${E^*}$
as above. Because the action of H on the polynomial ring
![]() $S({E^*})=S(V^*)^N$
is obtained from the action of G on
$S({E^*})=S(V^*)^N$
is obtained from the action of G on
![]() $S(V^*)$
, it preserves
$S(V^*)$
, it preserves
![]() $\mathbf {x}$
-degrees as well as
$\mathbf {x}$
-degrees as well as
![]() $\mathbf {N}$
-degrees. Therefore, we may choose the fundamental G-invariants
$\mathbf {N}$
-degrees. Therefore, we may choose the fundamental G-invariants
![]() ${G}_i(\mathbf {x})\in S(V^*)^G=(S(V^*)^N)^H=S({E^*})^H$
to be simultaneously
${G}_i(\mathbf {x})\in S(V^*)^G=(S(V^*)^N)^H=S({E^*})^H$
to be simultaneously
![]() $\mathbf {x}$
-homogeneous and
$\mathbf {x}$
-homogeneous and
![]() $\mathbf {N}$
-homogeneous, so that
$\mathbf {N}$
-homogeneous, so that
![]() ${H}_i(\mathbf {N}):={G}_i(\mathbf {x})$
form a set of
${H}_i(\mathbf {N}):={G}_i(\mathbf {x})$
form a set of
![]() $\mathbf {N}$
-homogeneous generators for the polynomial ring
$\mathbf {N}$
-homogeneous generators for the polynomial ring
![]() $S({E^*})^H$
. Because any algebraic relation
$S({E^*})^H$
. Because any algebraic relation
![]() $f({H}_1,\ldots ,{H}_r)=0$
would result in an algebraic relation
$f({H}_1,\ldots ,{H}_r)=0$
would result in an algebraic relation
![]() $f({G}_1,\ldots ,{G}_r)=0$
, the
$f({G}_1,\ldots ,{G}_r)=0$
, the
![]() $\mathbf {N}$
-homogeneous
$\mathbf {N}$
-homogeneous
![]() ${H}_i(\mathbf {N})$
must be algebraically independent. By Theorem 2.1, H is a complex reflection group.
${H}_i(\mathbf {N})$
must be algebraically independent. By Theorem 2.1, H is a complex reflection group.
Remark 3.1. As pointed out in [Reference Bessis, Bonnafé and Rouquier4, Proposition 3.16] and explained in [Reference Bonnafé, Lehrer and Michel7, Section 8.3], the action of H on
![]() ${E}$
is often not irreducible. Denote by
${E}$
is often not irreducible. Denote by
![]() ${\mathcal {D}_N}=\{d_1^N,\dots ,d_r^N\}$
the set of degrees
${\mathcal {D}_N}=\{d_1^N,\dots ,d_r^N\}$
the set of degrees
![]() $d_i^N:=\mathrm {deg}_{\mathbf {x}}({N}_i)$
. For
$d_i^N:=\mathrm {deg}_{\mathbf {x}}({N}_i)$
. For
![]() $d\in {\mathcal {D}_N}$
, let us write
$d\in {\mathcal {D}_N}$
, let us write
![]() $\mathbf {N}_d:=\{{N}_i\in \mathbf {N} \ | \ \mathrm {deg}_{\mathbf {x}}({N}_i)=d\}$
and
$\mathbf {N}_d:=\{{N}_i\in \mathbf {N} \ | \ \mathrm {deg}_{\mathbf {x}}({N}_i)=d\}$
and
![]() ${E^*_d}:={\mathrm {span}}_{\mathbb {C}}\mathbf {N}_d$
, so that
${E^*_d}:={\mathrm {span}}_{\mathbb {C}}\mathbf {N}_d$
, so that
![]() ${E^*}\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E^*_d}$
and
${E^*}\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E^*_d}$
and
![]() $S({E^*})\simeq \bigotimes _{d\in {\mathcal {D}_N}}S({E^*_d})$
as graded H-modules. For
$S({E^*})\simeq \bigotimes _{d\in {\mathcal {D}_N}}S({E^*_d})$
as graded H-modules. For
![]() $d\in {\mathcal {D}_N}$
, let
$d\in {\mathcal {D}_N}$
, let
![]() $H_{(d)}\subset \mathrm {GL}({E^*_d})$
denote the image of H in
$H_{(d)}\subset \mathrm {GL}({E^*_d})$
denote the image of H in
![]() $\mathrm {GL}({E^*_d})$
, so that H decomposes as a direct product
$\mathrm {GL}({E^*_d})$
, so that H decomposes as a direct product
![]() $\unicode{x2A09} _{d\in {\mathcal {D}_N}} H_{(d)}$
, where each
$\unicode{x2A09} _{d\in {\mathcal {D}_N}} H_{(d)}$
, where each
![]() $H_{(d)}$
is a reflection group on the graded dual
$H_{(d)}$
is a reflection group on the graded dual
![]() ${E}_{-d}$
of
${E}_{-d}$
of
![]() ${E^*_d}$
. We see that in fact there exist algebraically independent (bi)homogeneous polynomials
${E^*_d}$
. We see that in fact there exist algebraically independent (bi)homogeneous polynomials
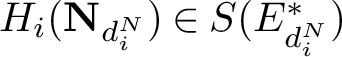 $\smash {{H}_i(\mathbf {N}_{d_i^N})\in S({E}^*_{d_i^N})}$
such that
$\smash {{H}_i(\mathbf {N}_{d_i^N})\in S({E}^*_{d_i^N})}$
such that
![]() $S({E^*})^H=\mathbb {C}[{H}_1,\dots ,{H}_r]$
, so that the fundamental G-invariants
$S({E^*})^H=\mathbb {C}[{H}_1,\dots ,{H}_r]$
, so that the fundamental G-invariants
![]() ${G}_1,\dots ,{G}_r$
generating
${G}_1,\dots ,{G}_r$
generating
![]() $S(V^*)^G=(S(V^*)^N)^H=S(E^*)^H$
can be expressed as
$S(V^*)^G=(S(V^*)^N)^H=S(E^*)^H$
can be expressed as
 $$ \begin{align} {G}_i(\mathbf{x})={H}_i(\mathbf{{N}}_{d_i^N}).\end{align} $$
$$ \begin{align} {G}_i(\mathbf{x})={H}_i(\mathbf{{N}}_{d_i^N}).\end{align} $$
Having chosen the fundamental G-invariants
![]() ${G}_i$
to have degrees
${G}_i$
to have degrees
![]() $d_1^G\leq \dots \leq d_r^G$
, we implicitly index the N-degrees
$d_1^G\leq \dots \leq d_r^G$
, we implicitly index the N-degrees
![]() $d_i^N$
and H-degrees
$d_i^N$
and H-degrees
![]() $d_i^H$
so that Equation (5) is satisfied.
$d_i^H$
so that Equation (5) is satisfied.
Remark 3.2. Unlike in the real case [Reference Bjorner and Brenti5, Reference Gal11], H is not necessarily (isomorphic to) a reflection subgroup of G or even a subgroup of G. A counterexample is given by
![]() $G_8=G \triangleright N=G(4,2,2)$
, so that
$G_8=G \triangleright N=G(4,2,2)$
, so that
![]() $G/N \simeq \mathfrak {S}_3$
– but
$G/N \simeq \mathfrak {S}_3$
– but
![]() $\mathfrak {S}_3$
is not a subgroup of
$\mathfrak {S}_3$
is not a subgroup of
![]() $G_8$
.
$G_8$
.
3.1 Harmonic polynomials
The space of N-harmonic polynomials
![]() ${\mathcal {C}_N}\subset S(V^*)$
is G-stable [Reference Lehrer and Taylor14, Proposition 12.2] and isomorphic to the regular representation of N [Reference Lehrer and Taylor14, Corollary 9.37]. The space of H-harmonic polynomials
${\mathcal {C}_N}\subset S(V^*)$
is G-stable [Reference Lehrer and Taylor14, Proposition 12.2] and isomorphic to the regular representation of N [Reference Lehrer and Taylor14, Corollary 9.37]. The space of H-harmonic polynomials
![]() ${\mathcal {C}_H}\subset S({E^*})$
is bigraded, by
${\mathcal {C}_H}\subset S({E^*})$
is bigraded, by
![]() $\mathbf {x}$
-degree as well as by
$\mathbf {x}$
-degree as well as by
![]() $\mathbf {N}$
-degree, and therefore it admits a
$\mathbf {N}$
-degree, and therefore it admits a
![]() $\mathbb {C}$
-basis of H-harmonic polynomials that are simultaneously
$\mathbb {C}$
-basis of H-harmonic polynomials that are simultaneously
![]() $\mathbf {x}$
-homogeneous and
$\mathbf {x}$
-homogeneous and
![]() $\mathbf {N}$
-homogeneous. The following result elaborates on [Reference Bonnafé, Lehrer and Michel7, Corollary 8.4] in our present setting.
$\mathbf {N}$
-homogeneous. The following result elaborates on [Reference Bonnafé, Lehrer and Michel7, Corollary 8.4] in our present setting.
Proposition 3.3. There is a graded G-module isomorphism
![]() ${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
such that
${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
such that
![]() $({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
as graded H-modules.
$({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
as graded H-modules.
Proof. Putting together the isomorphisms
![]() $S(V^*)\simeq S({E^*})\otimes {\mathcal {C}_N}$
as graded N-modules,
$S(V^*)\simeq S({E^*})\otimes {\mathcal {C}_N}$
as graded N-modules,
![]() $S({E^*})\simeq S({E^*})^H\otimes {\mathcal {C}_H}$
as bigraded H-modules (equivalently, as bigraded G-modules of N-invariants) and
$S({E^*})\simeq S({E^*})^H\otimes {\mathcal {C}_H}$
as bigraded H-modules (equivalently, as bigraded G-modules of N-invariants) and
![]() $S(V^*)^G=S({E^*})^H$
, we obtain the isomorphism
$S(V^*)^G=S({E^*})^H$
, we obtain the isomorphism
![]() $S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
as graded G-modules. Letting
$S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
as graded G-modules. Letting
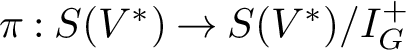 $\pi :S(V^*)\rightarrow S(V^*)/{I_G^+}$
denote the canonical projection, we see that
$\pi :S(V^*)\rightarrow S(V^*)/{I_G^+}$
denote the canonical projection, we see that
![]() $\mathbb {C}\otimes {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
must surject onto the image
$\mathbb {C}\otimes {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
must surject onto the image
 $S(V^*)/{I_G^+}\simeq {\mathcal {C}_G}$
, because
$S(V^*)/{I_G^+}\simeq {\mathcal {C}_G}$
, because
![]() $S(V^*)^G$
is generated as a
$S(V^*)^G$
is generated as a
![]() $\mathbb {C}$
-algebra by the generators of the ideal
$\mathbb {C}$
-algebra by the generators of the ideal
![]() ${I_G^+}$
. But this surjection
${I_G^+}$
. But this surjection
![]() ${\mathcal {C}_H}\otimes {\mathcal {C}_N}\rightarrow {\mathcal {C}_G}$
of graded G-modules must then be an isomorphism, because
${\mathcal {C}_H}\otimes {\mathcal {C}_N}\rightarrow {\mathcal {C}_G}$
of graded G-modules must then be an isomorphism, because
Because
![]() ${\mathcal {C}_H}\subset S({E^*})$
consists of N-invariants, we have
${\mathcal {C}_H}\subset S({E^*})$
consists of N-invariants, we have
![]() $({\mathcal {C}_H}\otimes {\mathcal {C}_N})^N={\mathcal {C}_H}\otimes ({\mathcal {C}_N})^N={\mathcal {C}_H}\otimes \mathbb {C}$
, and therefore
$({\mathcal {C}_H}\otimes {\mathcal {C}_N})^N={\mathcal {C}_H}\otimes ({\mathcal {C}_N})^N={\mathcal {C}_H}\otimes \mathbb {C}$
, and therefore
![]() $({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
as graded H-modules, as claimed.
$({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
as graded H-modules, as claimed.
Remark 3.4. It follows from the graded G-isomorphism
![]() $S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_G}$
that the Poincaré series of
$S(V^*)\simeq S(V^*)^G\otimes {\mathcal {C}_G}$
that the Poincaré series of
![]() ${\mathcal {C}_G}$
can be written as [Reference Chevalley9, Theorem B]
${\mathcal {C}_G}$
can be written as [Reference Chevalley9, Theorem B]
 $$ \begin{align*}\mathrm{Hilb}({\mathcal{C}_G};q) = \frac{\mathrm{Hilb}(S({V^*});q)}{\mathrm{Hilb}(S(V^*)^G;q)} = \prod_{i=1}^r\frac{1-q^{d_i^G}}{1-q}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}({\mathcal{C}_G};q) = \frac{\mathrm{Hilb}(S({V^*});q)}{\mathrm{Hilb}(S(V^*)^G;q)} = \prod_{i=1}^r\frac{1-q^{d_i^G}}{1-q}.\end{align*} $$
Because
![]() $|G|=d_1\cdots d_r$
, it is natural to ask for a combinatorial interpretation of
$|G|=d_1\cdots d_r$
, it is natural to ask for a combinatorial interpretation of
![]() $\mathrm {Hilb}({\mathcal {C}_G};q)$
as a weighted sum over the elements of G. When G is a real reflection group, G acts simply transitively on the connected components of its real hyperplane complement. Assigning some base connected component
$\mathrm {Hilb}({\mathcal {C}_G};q)$
as a weighted sum over the elements of G. When G is a real reflection group, G acts simply transitively on the connected components of its real hyperplane complement. Assigning some base connected component
![]() $R_e$
to the identity element
$R_e$
to the identity element
![]() $e \in G$
gives a bijection between group elements and connected components of the hyperplane complement
$e \in G$
gives a bijection between group elements and connected components of the hyperplane complement
![]() $g \leftrightarrow R_g$
, and we can define the statistic
$g \leftrightarrow R_g$
, and we can define the statistic
![]() $\mathrm {inv}(g)$
to be the number of inversions of
$\mathrm {inv}(g)$
to be the number of inversions of
![]() $g \in G$
; that is, the number of hyperplanes separating the connected component
$g \in G$
; that is, the number of hyperplanes separating the connected component
![]() $R_g$
from
$R_g$
from
![]() $R_e$
. In this case the Poincaré series of
$R_e$
. In this case the Poincaré series of
![]() ${\mathcal {C}_G}$
has the well-known interpretation (see for example [Reference Bjorner and Brenti5, Section 7.1] or [Reference Humphreys13, §3])
${\mathcal {C}_G}$
has the well-known interpretation (see for example [Reference Bjorner and Brenti5, Section 7.1] or [Reference Humphreys13, §3])
 $$ \begin{align*}\mathrm{Hilb}({\mathcal{C}_G};q) = \prod_{i=1}^r\frac{1-q^{d_i^G}}{1-q} = \sum_{g\in G} q^{\mathrm{inv}(g)}.\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}({\mathcal{C}_G};q) = \prod_{i=1}^r\frac{1-q^{d_i^G}}{1-q} = \sum_{g\in G} q^{\mathrm{inv}(g)}.\end{align*} $$
The graded G-module isomorphism
![]() ${\mathcal {C}_G} \simeq {\mathcal {C}_H} \otimes {\mathcal {C}_N}$
of Proposition 3.3 yields a factorisation
${\mathcal {C}_G} \simeq {\mathcal {C}_H} \otimes {\mathcal {C}_N}$
of Proposition 3.3 yields a factorisation
(bearing in mind that the quotient group
![]() $H=G/N$
acts by reflections on the graded vector space
$H=G/N$
acts by reflections on the graded vector space
![]() ${E}=V/N$
as detailed in Remark 3.1, and
${E}=V/N$
as detailed in Remark 3.1, and
![]() ${\mathcal {C}_H}$
is endowed with the resulting grading for Equation (6) to hold). This allows us to produce a combinatorial interpretation for
${\mathcal {C}_H}$
is endowed with the resulting grading for Equation (6) to hold). This allows us to produce a combinatorial interpretation for
![]() $\mathrm {Hilb}({\mathcal {C}_G};q)$
in some additional cases: provided prior combinatorial interpretations
$\mathrm {Hilb}({\mathcal {C}_G};q)$
in some additional cases: provided prior combinatorial interpretations
 $$ \begin{align*} \mathrm{Hilb}({\mathcal{C}_H};q)=\sum_{h\in H}q^{\mathrm{stat}_H(h)} \quad \text{and}\quad \mathrm{Hilb}({\mathcal{C}_N};q)=\sum_{n\in N}q^{\mathrm{stat}_N(n)},\end{align*} $$
$$ \begin{align*} \mathrm{Hilb}({\mathcal{C}_H};q)=\sum_{h\in H}q^{\mathrm{stat}_H(h)} \quad \text{and}\quad \mathrm{Hilb}({\mathcal{C}_N};q)=\sum_{n\in N}q^{\mathrm{stat}_N(n)},\end{align*} $$
we can then obtain an interpretation
 $$ \begin{align} \mathrm{Hilb}({\mathcal{C}_G};q)=\sum_{g\in G}q^{\mathrm{stat}_G(g)}=\sum_{h\in H}q^{\mathrm{stat}_H(h)}\left(\sum_{ n\in N} q^{\mathrm{stat}_N(n)}\right).\end{align} $$
$$ \begin{align} \mathrm{Hilb}({\mathcal{C}_G};q)=\sum_{g\in G}q^{\mathrm{stat}_G(g)}=\sum_{h\in H}q^{\mathrm{stat}_H(h)}\left(\sum_{ n\in N} q^{\mathrm{stat}_N(n)}\right).\end{align} $$
We will now illustrate this strategy with two concrete (and scaffolded) examples.
A combinatorial interpretation for
![]() $\mathrm {Hilb}(\mathcal {C}_{G(4,2,2)};q)$
is obtained from the choice of normal reflection subgroup
$\mathrm {Hilb}(\mathcal {C}_{G(4,2,2)};q)$
is obtained from the choice of normal reflection subgroup
 $$ \begin{align*}N=G(2,2,2)=\left\{\begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}, \begin{pmatrix} -1 & 0 \\ 0 & -1\end{pmatrix}\right\},\end{align*} $$
$$ \begin{align*}N=G(2,2,2)=\left\{\begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}, \begin{pmatrix} -1 & 0 \\ 0 & -1\end{pmatrix}\right\},\end{align*} $$
which is real and therefore admits the combinatorial interpretation described above in terms of the inversion statistic
![]() $\mathrm {Hilb}({\mathcal {C}_N};q)=1+q+q+q^2=(1+q)^2$
. Let us choose the coset representatives
$\mathrm {Hilb}({\mathcal {C}_N};q)=1+q+q+q^2=(1+q)^2$
. Let us choose the coset representatives
![]() $g_h\in G(4,2,2)$
for
$g_h\in G(4,2,2)$
for
![]() $h\in H\simeq C_2\times C_2$
to be
$h\in H\simeq C_2\times C_2$
to be
 $$ \begin{align*}\{g_{(1,1)},g_{(-1,1)},g_{(1,-1)},g_{(-1,-1)}\}=\left\{\begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}, \begin{pmatrix}0 & i \\ i & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix}, \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\right\}.\end{align*} $$
$$ \begin{align*}\{g_{(1,1)},g_{(-1,1)},g_{(1,-1)},g_{(-1,-1)}\}=\left\{\begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}, \begin{pmatrix}0 & i \\ i & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix}, \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\right\}.\end{align*} $$
Then we obtain the interpretation
 $$ \begin{align}\mathrm{Hilb}(\mathcal{C}_{G(4,2,2)};q)= (1+q^2)^2(1+q)^2=\sum_{g\in G(4,2,2)}q^{\mathrm{stat_{G(4,2,2)}(g)}} \end{align} $$
$$ \begin{align}\mathrm{Hilb}(\mathcal{C}_{G(4,2,2)};q)= (1+q^2)^2(1+q)^2=\sum_{g\in G(4,2,2)}q^{\mathrm{stat_{G(4,2,2)}(g)}} \end{align} $$
from Equation (7), because for each
![]() $h\in H$
the partial sum in Equation (8) over the coset
$h\in H$
the partial sum in Equation (8) over the coset
![]() $g_hN$
is given by
$g_hN$
is given by
 $$ \begin{align*} \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(1,1)+\mathrm{inv}_N(n)}=q^{0+0}+q^{0+1}+q^{0+1}+q^{0+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(-1,1)+\mathrm{inv}_N(n)}=q^{2+0}+q^{2+1}+q^{2+1}+q^{2+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(1,-1)+\mathrm{inv}_N(n)}=q^{2+0}+q^{2+1}+q^{2+1}+q^{2+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(-1,-1)+\mathrm{inv}_N(n)}=q^{4+0}+q^{4+1}+q^{4+1}+q^{4+2}. \end{align*} $$
$$ \begin{align*} \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(1,1)+\mathrm{inv}_N(n)}=q^{0+0}+q^{0+1}+q^{0+1}+q^{0+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(-1,1)+\mathrm{inv}_N(n)}=q^{2+0}+q^{2+1}+q^{2+1}+q^{2+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(1,-1)+\mathrm{inv}_N(n)}=q^{2+0}+q^{2+1}+q^{2+1}+q^{2+2};\\ \sum_{n \in N}q^{2\cdot\mathrm{inv}_{C_2\times C_2}(-1,-1)+\mathrm{inv}_N(n)}=q^{4+0}+q^{4+1}+q^{4+1}+q^{4+2}. \end{align*} $$
The factor of
![]() $2$
in
$2$
in
![]() $2\cdot \mathrm {inv}_{C_2\times C_2}$
above arises from the grading on the reflection representation
$2\cdot \mathrm {inv}_{C_2\times C_2}$
above arises from the grading on the reflection representation
![]() ${E}$
of
${E}$
of
![]() $H\simeq C_2\times C_2$
as described in Remark 3.1: in this case we have that
$H\simeq C_2\times C_2$
as described in Remark 3.1: in this case we have that
![]() ${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^2+y^2,xy\}$
is homogeneous of degree
${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^2+y^2,xy\}$
is homogeneous of degree
![]() $2$
.
$2$
.
We can similarly obtain a combinatorial interpretation for
 $$ \begin{align}\mathrm{Hilb}(\mathcal{C}_{G_9};q)=\left(\frac{1-q^8}{1-q}\right)\left(\frac{1-q^{24}}{1-q}\right)=\sum_{g\in G_9}q^{\mathrm{stat}_{G_9}(g)}\end{align} $$
$$ \begin{align}\mathrm{Hilb}(\mathcal{C}_{G_9};q)=\left(\frac{1-q^8}{1-q}\right)\left(\frac{1-q^{24}}{1-q}\right)=\sum_{g\in G_9}q^{\mathrm{stat}_{G_9}(g)}\end{align} $$
from the choice of normal reflection subgroup
![]() $N=G(4,2,2)$
, which has the combinatorial interpretation
$N=G(4,2,2)$
, which has the combinatorial interpretation
 $\mathrm {Hilb}({\mathcal {C}_N};q)=\sum _{n\in N}q^{\mathrm {stat}_N(n)}$
obtained in the previous example, and
$\mathrm {Hilb}({\mathcal {C}_N};q)=\sum _{n\in N}q^{\mathrm {stat}_N(n)}$
obtained in the previous example, and
![]() $H\simeq G(6,6,2)$
, which is isomorphic as a reflection group to the dihedral group of order
$H\simeq G(6,6,2)$
, which is isomorphic as a reflection group to the dihedral group of order
![]() $12$
and is therefore real and admits the combinatorial interpretation
$12$
and is therefore real and admits the combinatorial interpretation
 $$ \begin{align*}\mathrm{Hilb}(\mathcal{C}_{G(6,6,2)};q)=\left(\frac{1-q^2}{1-q}\right)\left(\frac{1-q^6}{1-q}\right)=\sum_{h\in G(6,6,2)}q^{\mathrm{inv}_{G(6,6,2)}(h)} .\end{align*} $$
$$ \begin{align*}\mathrm{Hilb}(\mathcal{C}_{G(6,6,2)};q)=\left(\frac{1-q^2}{1-q}\right)\left(\frac{1-q^6}{1-q}\right)=\sum_{h\in G(6,6,2)}q^{\mathrm{inv}_{G(6,6,2)}(h)} .\end{align*} $$
Now given a choice of coset representatives
![]() $g_h\in G_9$
for each
$g_h\in G_9$
for each
![]() $h\in H\simeq G(6,6,2)$
we can define, for each
$h\in H\simeq G(6,6,2)$
we can define, for each
![]() $g=g_hn\in g_hN$
,
$g=g_hn\in g_hN$
,
which is seen to satisfy Equation (9). The factor of
![]() $4$
in
$4$
in
![]() $4\cdot \mathrm {inv}_{G(6,6,2)}$
above arises from the grading on the reflection representation
$4\cdot \mathrm {inv}_{G(6,6,2)}$
above arises from the grading on the reflection representation
![]() ${E}$
of
${E}$
of
![]() $H\simeq G(6,6,2)$
as described in Remark 3.1: in this case
$H\simeq G(6,6,2)$
as described in Remark 3.1: in this case
![]() ${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^4+y^4,x^2y^2\}$
is homogeneous of degree
${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^4+y^4,x^2y^2\}$
is homogeneous of degree
![]() $4$
.
$4$
.
Remark 3.5. It follows from Proposition 3.3 that for any G-module M the (dual) Orlik-Solomon space
![]() ${(U_M^N)^*}=({\mathcal {C}_N}\otimes M^*)^N$
as in Definition 2.9 can be considered as an H-module or (equivalently) as a G-module of N-invariants.
${(U_M^N)^*}=({\mathcal {C}_N}\otimes M^*)^N$
as in Definition 2.9 can be considered as an H-module or (equivalently) as a G-module of N-invariants.
The following result is useful in determining the Orlik-Solomon space
![]() ${U_M^N}$
in particular examples (cf. Section 7) up to graded G-module isomorphism.
${U_M^N}$
in particular examples (cf. Section 7) up to graded G-module isomorphism.
Lemma 3.6. Let
![]() $\eta _N: S(V^*)\rightarrow {\mathcal {C}_N}$
denote the G-equivariant projection onto the space of N-harmonic polynomials. Let M be a G-module of rank m, and suppose that
$\eta _N: S(V^*)\rightarrow {\mathcal {C}_N}$
denote the G-equivariant projection onto the space of N-harmonic polynomials. Let M be a G-module of rank m, and suppose that
![]() $\tilde {u}_1,\dots ,\tilde {u}_m$
form a homogeneous basis for
$\tilde {u}_1,\dots ,\tilde {u}_m$
form a homogeneous basis for
![]() $(S(V^*)\otimes M^*)^N$
as a free
$(S(V^*)\otimes M^*)^N$
as a free
![]() $S(V^*)^N$
-module such that
$S(V^*)^N$
-module such that
 $(\tilde {U}_M^N)^*:={\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1,\dots ,\tilde {u}_m\}$
is G-stable. Then the restriction of the projection
$(\tilde {U}_M^N)^*:={\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1,\dots ,\tilde {u}_m\}$
is G-stable. Then the restriction of the projection
 $\eta _N\otimes 1:(\tilde {U}_M^N)^*\rightarrow {(U_M^N)^*}$
is a graded G-module isomorphism.
$\eta _N\otimes 1:(\tilde {U}_M^N)^*\rightarrow {(U_M^N)^*}$
is a graded G-module isomorphism.
Proof. Let
![]() $u_1,\dots ,u_m$
be a homogeneous basis for
$u_1,\dots ,u_m$
be a homogeneous basis for
![]() ${(U_M^N)^*}:=({\mathcal {C}_N}\otimes M^*)^N$
. We may assume that
${(U_M^N)^*}:=({\mathcal {C}_N}\otimes M^*)^N$
. We may assume that
![]() $\mathrm {deg}(u_i)=e_i^N(M)=\mathrm {deg}(\tilde {u}_i)$
for each
$\mathrm {deg}(u_i)=e_i^N(M)=\mathrm {deg}(\tilde {u}_i)$
for each
![]() $i=1,\dots ,m$
. Let
$i=1,\dots ,m$
. Let
![]() $y_1,\dots ,y_m$
be a basis for
$y_1,\dots ,y_m$
be a basis for
![]() $M^*$
, and write
$M^*$
, and write
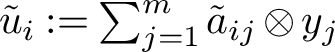 $\tilde {u}_i:=\sum _{j=1}^m\tilde {a}_{ij}\otimes y_j$
and
$\tilde {u}_i:=\sum _{j=1}^m\tilde {a}_{ij}\otimes y_j$
and
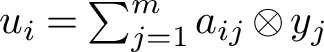 $u_i=\sum _{j=1}^ma_{ij}\otimes y_j$
, where
$u_i=\sum _{j=1}^ma_{ij}\otimes y_j$
, where
![]() $\tilde {a}_{ij}\in S(V^*)$
and
$\tilde {a}_{ij}\in S(V^*)$
and
![]() $a_{ij}\in {\mathcal {C}_N}$
and every nonzero
$a_{ij}\in {\mathcal {C}_N}$
and every nonzero
![]() $\tilde {a}_{ij}$
and
$\tilde {a}_{ij}$
and
![]() $a_{ij}$
is homogeneous of degree
$a_{ij}$
is homogeneous of degree
![]() $e_i^N(M)$
. Because the
$e_i^N(M)$
. Because the
![]() $\tilde {u}_i$
and the
$\tilde {u}_i$
and the
![]() $u_i$
form bases for
$u_i$
form bases for
![]() $(S(V^*)\otimes M^*)^N$
as a free
$(S(V^*)\otimes M^*)^N$
as a free
![]() $S(V^*)^N$
-module, there exists a matrix
$S(V^*)^N$
-module, there exists a matrix
![]() $[p_{ij}]\in \mathrm {GL}_m(S(V^*)^N)$
such that
$[p_{ij}]\in \mathrm {GL}_m(S(V^*)^N)$
such that
![]() $[\tilde {a}_{ij}]=[p_{ij}]\cdot [a_{ij}]$
. Because the kernel of
$[\tilde {a}_{ij}]=[p_{ij}]\cdot [a_{ij}]$
. Because the kernel of
![]() $\eta _N:S(V^*)\rightarrow {\mathcal {C}_N}$
is precisely the ideal generated by homogeneous N-invariants of positive degree, it follows that
$\eta _N:S(V^*)\rightarrow {\mathcal {C}_N}$
is precisely the ideal generated by homogeneous N-invariants of positive degree, it follows that
![]() $[\eta _N(\tilde {a}_{ij})]=[p_{ij}(0)]\cdot [a_{ij}]$
, where
$[\eta _N(\tilde {a}_{ij})]=[p_{ij}(0)]\cdot [a_{ij}]$
, where
![]() $p_{ij}(0)$
denotes the evaluation at
$p_{ij}(0)$
denotes the evaluation at
![]() $0\in V$
. Because
$0\in V$
. Because
![]() $\mathrm {deg}(\mathrm {det}[\tilde {a}_{ij}])=\sum _{i=1}^m e_i^N(M)=\mathrm {deg}(\mathrm {det}[a_{ij}])$
, it follows that
$\mathrm {deg}(\mathrm {det}[\tilde {a}_{ij}])=\sum _{i=1}^m e_i^N(M)=\mathrm {deg}(\mathrm {det}[a_{ij}])$
, it follows that
![]() $\mathrm {det}[p_{ij}]\in \mathbb {C}^\times $
, and therefore
$\mathrm {det}[p_{ij}]\in \mathbb {C}^\times $
, and therefore
![]() $[p_{ij}(0)]\in \mathrm {GL}_m(\mathbb {C})$
. Because
$[p_{ij}(0)]\in \mathrm {GL}_m(\mathbb {C})$
. Because
![]() $\eta _N\otimes 1$
is G-equivariant and
$\eta _N\otimes 1$
is G-equivariant and
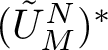 $(\tilde {U}_M^N)^*$
is G-stable,
$(\tilde {U}_M^N)^*$
is G-stable,
 $\eta _N\otimes 1:(\tilde {U}_M^N)^*\rightarrow {(U_M^N)^*}$
is a graded isomorphism of G-modules.
$\eta _N\otimes 1:(\tilde {U}_M^N)^*\rightarrow {(U_M^N)^*}$
is a graded isomorphism of G-modules.
3.2 Numerology
The following consequence of Proposition 3.3 establishes the first equation of Theorem 1.3 in more generality.
Corollary 3.7. Let M be a G-module and define
![]() ${U_M^N}$
as in Definition 2.9. For a suitable choice of indexing we have
${U_M^N}$
as in Definition 2.9. For a suitable choice of indexing we have
Proof. Applying Proposition 3.3, we see that
Let m be the rank of M, and let
![]() $y_1,\dots ,y_m$
be a basis of
$y_1,\dots ,y_m$
be a basis of
![]() $M^*$
. Let
$M^*$
. Let
 $a_{ij}^N\in {\mathcal {C}_N}$
be
$a_{ij}^N\in {\mathcal {C}_N}$
be
![]() $\mathbf {x}$
-homogeneous such that
$\mathbf {x}$
-homogeneous such that
 $u_i^N:=\sum _{j=1}^ma_{ij}^N\otimes y_j$
form a basis for
$u_i^N:=\sum _{j=1}^ma_{ij}^N\otimes y_j$
form a basis for
![]() ${(U_M^N)^*}$
with
${(U_M^N)^*}$
with
![]() $\mathrm {deg}_{\mathbf {x}}(u_i^N)=e_i^N(M)$
. Letting
$\mathrm {deg}_{\mathbf {x}}(u_i^N)=e_i^N(M)$
. Letting
![]() ${\mathcal {E}_M^N}:=\{e_1^N(M),\dots ,e_m^N(M)\}$
denote the set of M-exponents of N, we see that
${\mathcal {E}_M^N}:=\{e_1^N(M),\dots ,e_m^N(M)\}$
denote the set of M-exponents of N, we see that
 $$ \begin{align*}{(U_M^N)^*}\simeq\bigoplus_{e\in{\mathcal{E}_M^N}}{(U_M^N)^*_e}\end{align*} $$
$$ \begin{align*}{(U_M^N)^*}\simeq\bigoplus_{e\in{\mathcal{E}_M^N}}{(U_M^N)^*_e}\end{align*} $$
as an H-module. Therefore, there exist
![]() $\mathbf {x}$
-homogeneous
$\mathbf {x}$
-homogeneous
 $a_{ij}^H\in {\mathcal {C}_H}$
such that
$a_{ij}^H\in {\mathcal {C}_H}$
such that
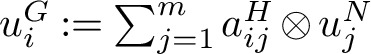 $u_i^G:=\sum _{j=1}^ma_{ij}^H\otimes u_j^N$
form a basis for
$u_i^G:=\sum _{j=1}^ma_{ij}^H\otimes u_j^N$
form a basis for
![]() $({\mathcal {C}_H}\otimes {(U_M^N)^*})^H$
with
$({\mathcal {C}_H}\otimes {(U_M^N)^*})^H$
with
![]() $\mathrm {deg}_{\mathbf {x}}(u_i^G)=e_i^G(U_M^N)$
and such that
$\mathrm {deg}_{\mathbf {x}}(u_i^G)=e_i^G(U_M^N)$
and such that
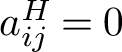 $a_{ij}^H=0$
whenever
$a_{ij}^H=0$
whenever
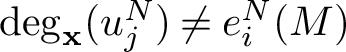 $\mathrm {deg}_{\mathbf {x}}(u_j^N)\neq e_i^N(M)$
(in other words, the
$\mathrm {deg}_{\mathbf {x}}(u_j^N)\neq e_i^N(M)$
(in other words, the
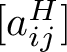 $[a_{ij}^H]$
may be chosen to be square-diagonal corresponding to the graded decomposition of
$[a_{ij}^H]$
may be chosen to be square-diagonal corresponding to the graded decomposition of
![]() ${(U_M^N)^*}$
). But then the
${(U_M^N)^*}$
). But then the
![]() $u_i^G$
form an
$u_i^G$
form an
![]() $\mathbf {x}$
-homogeneous basis for
$\mathbf {x}$
-homogeneous basis for
![]() $({\mathcal {C}_G}\otimes M^*)^G\simeq ({\mathcal {C}_H}\otimes (U_M^N)^*)^H$
, and we see that
$({\mathcal {C}_G}\otimes M^*)^G\simeq ({\mathcal {C}_H}\otimes (U_M^N)^*)^H$
, and we see that
3.3 Amenability
Recall from Section 2.4 that a G-module M of rank m is called amenable if
![]() $\sum _{i=1}^m e_i^G(M)=e_1^G(\bigwedge ^mM)$
.
$\sum _{i=1}^m e_i^G(M)=e_1^G(\bigwedge ^mM)$
.
Remark 3.8. Regardless of whether a G-module M of rank m is amenable, we always have a natural
![]() $S(V^*)^G$
-linear injective homomorphism
$S(V^*)^G$
-linear injective homomorphism
in
![]() $(S(V^*)\otimes \bigwedge M^*)^G$
, which identifies
$(S(V^*)\otimes \bigwedge M^*)^G$
, which identifies
![]() $\bigwedge ^m({\mathcal {C}_G}\otimes M^*)^G$
with
$\bigwedge ^m({\mathcal {C}_G}\otimes M^*)^G$
with
![]() $a\otimes ({\mathcal {C}_G}\otimes \bigwedge ^m M^*)^G$
for some
$a\otimes ({\mathcal {C}_G}\otimes \bigwedge ^m M^*)^G$
for some
![]() $0\neq a\in S(V^*)^G$
. The amenability of M as a G-module is therefore precisely the requirement that
$0\neq a\in S(V^*)^G$
. The amenability of M as a G-module is therefore precisely the requirement that
![]() $a\in \mathbb {C}$
be a constant polynomial. For brevity and convenience, we will summarise this equivalent characterisation of amenability in the following Lemma 3.9 (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 2.10]).
$a\in \mathbb {C}$
be a constant polynomial. For brevity and convenience, we will summarise this equivalent characterisation of amenability in the following Lemma 3.9 (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 2.10]).
Lemma 3.9. A G-module M of rank m is amenable if and only if
The decomposition
![]() ${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
from Proposition 3.3 and its Corollary 3.7 have many useful consequences. Although the following result can be proved more directly by appealing to [Reference Bonnafé, Lehrer and Michel7, Corollary 8.7], we provide a full proof.
${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
from Proposition 3.3 and its Corollary 3.7 have many useful consequences. Although the following result can be proved more directly by appealing to [Reference Bonnafé, Lehrer and Michel7, Corollary 8.7], we provide a full proof.
Lemma 3.10. Let M be an H-module. Then
-
(i)
 $({\mathcal {C}_G}\otimes M^*)^G\simeq ({\mathcal {C}_H}\otimes M^*)^H$
and
$({\mathcal {C}_G}\otimes M^*)^G\simeq ({\mathcal {C}_H}\otimes M^*)^H$
and -
(ii) M is amenable as a G-module if and only if M is amenable as an H-module.
Proof. The M-exponents
![]() $e_i^G(M)$
of G are obtained as the
$e_i^G(M)$
of G are obtained as the
![]() $\mathbf {x}$
-degrees of any
$\mathbf {x}$
-degrees of any
![]() $\mathbf {x}$
-homogeneous basis for
$\mathbf {x}$
-homogeneous basis for
![]() $({\mathcal {C}_G}\otimes M^*)$
, and the M-exponents
$({\mathcal {C}_G}\otimes M^*)$
, and the M-exponents
![]() $e_i^H(M)$
of H are analogously obtained as the
$e_i^H(M)$
of H are analogously obtained as the
![]() $\mathbf {N}$
-degrees of any (bi)homogeneous basis for
$\mathbf {N}$
-degrees of any (bi)homogeneous basis for
![]() $({\mathcal {C}_H}\otimes M^*)^H$
. Letting m denote the rank of M, the exponent
$({\mathcal {C}_H}\otimes M^*)^H$
. Letting m denote the rank of M, the exponent
![]() $e_1^G(\bigwedge ^m M)$
is the
$e_1^G(\bigwedge ^m M)$
is the
![]() $\mathbf {x}$
-degree of a basis element for
$\mathbf {x}$
-degree of a basis element for
![]() $({\mathcal {C}_G}\otimes \bigwedge ^m M^*)^G$
, and the exponent
$({\mathcal {C}_G}\otimes \bigwedge ^m M^*)^G$
, and the exponent
![]() $e_i^H(\bigwedge ^m M)$
is the
$e_i^H(\bigwedge ^m M)$
is the
![]() $\mathbf {N}$
-degree of a basis element for
$\mathbf {N}$
-degree of a basis element for
![]() $({\mathcal {C}_H}\otimes \bigwedge ^m M^*)^H$
. Because both M and
$({\mathcal {C}_H}\otimes \bigwedge ^m M^*)^H$
. Because both M and
![]() ${\mathcal {C}_H}$
are N-invariant, and
${\mathcal {C}_H}$
are N-invariant, and
![]() ${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
as graded G-modules such that
${\mathcal {C}_G}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}$
as graded G-modules such that
![]() $({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
by Proposition 3.3, we obtain
$({\mathcal {C}_G})^N\simeq {\mathcal {C}_H}$
by Proposition 3.3, we obtain
which establishes (i).
Applying (i) to
![]() $\bigwedge ^mM^*$
, we have that
$\bigwedge ^mM^*$
, we have that
![]() $({\mathcal {C}_G}\otimes {\textstyle \bigwedge ^m}M^*)^G\simeq ({\mathcal {C}_H}\otimes {\textstyle \bigwedge ^m}M^*)^H$
. By Lemma 3.9, the amenability of M as a G-module and the amenability of M as an H-module are respectively equivalent to
$({\mathcal {C}_G}\otimes {\textstyle \bigwedge ^m}M^*)^G\simeq ({\mathcal {C}_H}\otimes {\textstyle \bigwedge ^m}M^*)^H$
. By Lemma 3.9, the amenability of M as a G-module and the amenability of M as an H-module are respectively equivalent to
which proves (ii).
Remark 3.11. Because the Orlik-Solomon space
![]() ${U_M^N}$
of Definition 2.9 is trivial as an N-module, it follows from Lemma 3.10 that
${U_M^N}$
of Definition 2.9 is trivial as an N-module, it follows from Lemma 3.10 that
![]() ${U_M^N}$
is amenable as a G-module if and only if it is amenable as an H-module. From now on we will just say that
${U_M^N}$
is amenable as a G-module if and only if it is amenable as an H-module. From now on we will just say that
![]() ${U_M^N}$
is amenable whenever these equivalent conditions hold.
${U_M^N}$
is amenable whenever these equivalent conditions hold.
Proposition 3.12. Let M be a G-module and define
![]() ${U_M^N}$
as in Definition 2.9.
${U_M^N}$
as in Definition 2.9.
-
(i) If M is amenable as a G-module, then
 ${U_M^N}$
is amenable.
${U_M^N}$
is amenable. -
(ii) If M is amenable as an N-module and
 ${U_M^N}$
is amenable, then M is amenable as a G-module.
${U_M^N}$
is amenable, then M is amenable as a G-module.
Proof. Let m denote the rank of M. Define the amenability defects
 $$ \begin{gather*} \gamma:=\sum_{i=1}^m e_i^G(M)-e_1^G({\textstyle\bigwedge^m} M);\qquad \nu:=\sum_{i=1}^me_i^N(M)-e_1^N({\textstyle\bigwedge^m}M);\qquad \text{and}\\ \eta:=\sum_{i=1}^m e_i^G(U_M^N)-e_1^G({\textstyle\bigwedge^m}U_M^N), \end{gather*} $$
$$ \begin{gather*} \gamma:=\sum_{i=1}^m e_i^G(M)-e_1^G({\textstyle\bigwedge^m} M);\qquad \nu:=\sum_{i=1}^me_i^N(M)-e_1^N({\textstyle\bigwedge^m}M);\qquad \text{and}\\ \eta:=\sum_{i=1}^m e_i^G(U_M^N)-e_1^G({\textstyle\bigwedge^m}U_M^N), \end{gather*} $$
so that M is amenable as a G-module if and only if
![]() $\gamma =0$
, M is amenable as an N-module if and only if
$\gamma =0$
, M is amenable as an N-module if and only if
![]() $\nu =0$
and
$\nu =0$
and
![]() ${U_M^N}$
is amenable as a G-module if and only if
${U_M^N}$
is amenable as a G-module if and only if
![]() $\eta =0$
. By Lemma 3.10,
$\eta =0$
. By Lemma 3.10,
![]() ${U_M^N}$
is also amenable as an H-module if and only if
${U_M^N}$
is also amenable as an H-module if and only if
![]() $\eta =0$
. By [Reference Orlik and Solomon16, Lemma 2.8] (see also Remark 3.8), in any case we have that
$\eta =0$
. By [Reference Orlik and Solomon16, Lemma 2.8] (see also Remark 3.8), in any case we have that
![]() $\gamma ,\nu ,\eta \geq 0$
.
$\gamma ,\nu ,\eta \geq 0$
.
Let
![]() $W_M^N$
be the dual of
$W_M^N$
be the dual of
![]() $(W_M^N)^*:=({\mathcal {C}_N}\otimes {\textstyle \bigwedge ^m}M^*)^N$
(instead of the more natural but cumbersome
$(W_M^N)^*:=({\mathcal {C}_N}\otimes {\textstyle \bigwedge ^m}M^*)^N$
(instead of the more natural but cumbersome
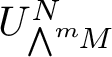 $U_{\bigwedge ^m\!\! M}^N$
in lieu of
$U_{\bigwedge ^m\!\! M}^N$
in lieu of
![]() $W_M^N$
). From Corollary 3.7, we know that
$W_M^N$
). From Corollary 3.7, we know that
Summing the first equation over
![]() $i=1,\dots ,m$
and subtracting the second equation, we obtain
$i=1,\dots ,m$
and subtracting the second equation, we obtain
Consider now the natural inclusion of graded G-modules
in
![]() $(S(V^*)\otimes \bigwedge M^*)^N$
, which identifies
$(S(V^*)\otimes \bigwedge M^*)^N$
, which identifies
![]() $\bigwedge ^m(U_M^N)^*$
with
$\bigwedge ^m(U_M^N)^*$
with
![]() $a\otimes (W_M^N)^*$
as graded G-modules for some
$a\otimes (W_M^N)^*$
as graded G-modules for some
![]() $\mathbf {x}$
-homogeneous
$\mathbf {x}$
-homogeneous
![]() $a\in S({E^*})$
with
$a\in S({E^*})$
with
![]() $\mathrm {deg}_{\mathbf {x}}(a)=\nu $
(cf. Remark 3.8). From this it follows that
$\mathrm {deg}_{\mathbf {x}}(a)=\nu $
(cf. Remark 3.8). From this it follows that
![]() $e_1^G(\bigwedge ^m U_M^N)+\nu \geq e_1^G(W_M^N)$
, which together with Equation (10) implies that
$e_1^G(\bigwedge ^m U_M^N)+\nu \geq e_1^G(W_M^N)$
, which together with Equation (10) implies that
![]() $\eta \leq \gamma $
. Therefore, if M is amenable as a G-module, then
$\eta \leq \gamma $
. Therefore, if M is amenable as a G-module, then
![]() $U_M^N$
is amenable. If M is amenable as an N-module, so that
$U_M^N$
is amenable. If M is amenable as an N-module, so that
![]() $\nu =0$
, then we see that
$\nu =0$
, then we see that
![]() $\bigwedge ^m{(U_M^N)^*}\simeq (W_M^N)^*$
as G-modules. Therefore,
$\bigwedge ^m{(U_M^N)^*}\simeq (W_M^N)^*$
as G-modules. Therefore,
![]() $e_1^G(\bigwedge ^m{U_M^N})= e_1^G(W_M^N)$
, and we obtain from Equation (10) that
$e_1^G(\bigwedge ^m{U_M^N})= e_1^G(W_M^N)$
, and we obtain from Equation (10) that
![]() $\eta =\gamma $
in this case. Hence, if M is amenable as an N-module and
$\eta =\gamma $
in this case. Hence, if M is amenable as an N-module and
![]() ${U_M^N}$
is amenable, then M is amenable as a G-module.
${U_M^N}$
is amenable, then M is amenable as a G-module.
Remark 3.13. It is not true in general that M being amenable as a G-module implies that M is amenable as an N-module. For a counterexample, let
![]() $G=C_a=\langle c\rangle $
and
$G=C_a=\langle c\rangle $
and
![]() $N=C_d=\langle c^e\rangle $
with
$N=C_d=\langle c^e\rangle $
with
![]() $a=de$
, acting on
$a=de$
, acting on
![]() $V=\mathbb {C}$
in the standard reflection representation by
$V=\mathbb {C}$
in the standard reflection representation by
![]() $c\mapsto \zeta _a$
, a primitive ath root of unity. Consider the G-module
$c\mapsto \zeta _a$
, a primitive ath root of unity. Consider the G-module
![]() $M:=V^*\oplus (V^*)^{\otimes (d-1)}$
, so that
$M:=V^*\oplus (V^*)^{\otimes (d-1)}$
, so that
 $\bigwedge ^2M\simeq (V^*)^{\otimes d}$
. Then
$\bigwedge ^2M\simeq (V^*)^{\otimes d}$
. Then
![]() $e_1^G(M)=1=e_1^N(M)$
and
$e_1^G(M)=1=e_1^N(M)$
and
![]() $e_2^G(M)=d-1=e_2^N(M)$
. Because
$e_2^G(M)=d-1=e_2^N(M)$
. Because
 $e_1^G(\bigwedge ^2 M)=d=e_1^G(M)+e_2^G(M)$
, M is amenable as a G-module. However,
$e_1^G(\bigwedge ^2 M)=d=e_1^G(M)+e_2^G(M)$
, M is amenable as a G-module. However,
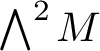 $\bigwedge ^2M$
is trivial as an N-module, and therefore
$\bigwedge ^2M$
is trivial as an N-module, and therefore
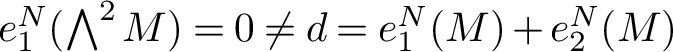 $e_1^N(\bigwedge ^2 M)=0\neq d=e_1^N(M)+e_2^N(M)$
, so M is not amenable as an N-module.
$e_1^N(\bigwedge ^2 M)=0\neq d=e_1^N(M)+e_2^N(M)$
, so M is not amenable as an N-module.
3.4 Poincaré Series
Suppose that M is an amenable G-module of rank m. Then by Proposition 3.12 and Lemma 3.10, the Orlik-Solomon space
![]() ${U_M^N}$
of Definition 2.9 is amenable (considered either as a G-module or as an H-module). Let us again write
${U_M^N}$
of Definition 2.9 is amenable (considered either as a G-module or as an H-module). Let us again write
![]() ${\mathcal {E}_M^N}:=\{e_1^N(M),\dots ,e_m(M)\}$
for the set of M-exponents of N. We have a graded G-module decomposition
${\mathcal {E}_M^N}:=\{e_1^N(M),\dots ,e_m(M)\}$
for the set of M-exponents of N. We have a graded G-module decomposition
 $$ \begin{align*}{(U_M^N)^*}=\bigoplus_{e\in{\mathcal{E}_M^N}}{(U_M^N)^*_e},\end{align*} $$
$$ \begin{align*}{(U_M^N)^*}=\bigoplus_{e\in{\mathcal{E}_M^N}}{(U_M^N)^*_e},\end{align*} $$
from which we obtain more generally a graded G-module decomposition of
![]() $\bigwedge ^p{(U_M^N)^*}$
:
$\bigwedge ^p{(U_M^N)^*}$
:
 $$ \begin{align*}\bigl({\textstyle\bigwedge^p}{(U_M^N)^*}\bigr)_e:={\mathrm{span}}_{\mathbb{C}}\left\{u_{i_1}\wedge\dots\wedge u_{i_p} \ \middle| \ u_{i_j}\in \bigl(U_M^N\bigr)^*_{e_j} \ \text{with} \ {\textstyle\sum_{j=1}^p} e_j=e\right\}.\end{align*} $$
$$ \begin{align*}\bigl({\textstyle\bigwedge^p}{(U_M^N)^*}\bigr)_e:={\mathrm{span}}_{\mathbb{C}}\left\{u_{i_1}\wedge\dots\wedge u_{i_p} \ \middle| \ u_{i_j}\in \bigl(U_M^N\bigr)^*_{e_j} \ \text{with} \ {\textstyle\sum_{j=1}^p} e_j=e\right\}.\end{align*} $$
This results in an obvious bigrading of
![]() $\bigwedge {(U_M^N)^*}$
and a corresponding trigrading of the associative algebra
$\bigwedge {(U_M^N)^*}$
and a corresponding trigrading of the associative algebra
![]() $S({V^*})\otimes \bigwedge {(U_M^N)^*}$
.
$S({V^*})\otimes \bigwedge {(U_M^N)^*}$
.
Definition 3.14. The trigraded Poincaré series for
![]() $(S(V^*)\otimes \bigwedge {(U_M^N)^*})^G$
is
$(S(V^*)\otimes \bigwedge {(U_M^N)^*})^G$
is
 $$ \begin{align*}\mathcal{P}^G_M(x,y,u):=\sum_{\ell,e,p\geq 0}\mathrm{dim}_{\mathbb{C}}\left(S(V^*)_\ell\otimes\left({\textstyle\bigwedge^p}{(U_M^N)^*}\right)_e\right)^G x^\ell y^e u^p.\end{align*} $$
$$ \begin{align*}\mathcal{P}^G_M(x,y,u):=\sum_{\ell,e,p\geq 0}\mathrm{dim}_{\mathbb{C}}\left(S(V^*)_\ell\otimes\left({\textstyle\bigwedge^p}{(U_M^N)^*}\right)_e\right)^G x^\ell y^e u^p.\end{align*} $$
We will follow the usual strategy of computing this Poincaré series in two different ways to deduce combinatorial formulas. Let us denote as before
![]() $d_1^G,\dots ,d_r^G$
the degrees of the fundamental G-invariants generating
$d_1^G,\dots ,d_r^G$
the degrees of the fundamental G-invariants generating
![]() $S(V^*)^G$
as a polynomial algebra. Let us index the M-exponents of N,
$S(V^*)^G$
as a polynomial algebra. Let us index the M-exponents of N,
![]() $e_1^N(M),\dots ,e_m^N(M)$
, and the
$e_1^N(M),\dots ,e_m^N(M)$
, and the
![]() ${U_M^N}$
-exponents of G,
${U_M^N}$
-exponents of G,
![]() $e_1^G({U_M^N}),\dots ,e_m^G({U_M^N})$
, as in Corollary 3.7, so that
$e_1^G({U_M^N}),\dots ,e_m^G({U_M^N})$
, as in Corollary 3.7, so that
![]() $e_i^N(M)+e_i^G({U_M^N})=e_i^G(M)$
.
$e_i^N(M)+e_i^G({U_M^N})=e_i^G(M)$
.
Proposition 3.15.
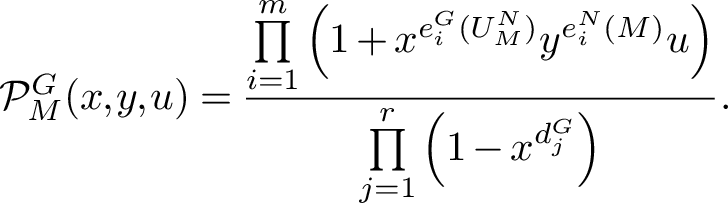 $\mathcal {P}^G_M(x,y,u)=\displaystyle \frac {\prod \limits _{i=1}^m\left (1+x^{e_i^G({U_M^N})}y^{e_i^N(M)}u\right )}{\prod \limits _{j=1}^r\left (1-x^{d_j^G}\right )}.$
$\mathcal {P}^G_M(x,y,u)=\displaystyle \frac {\prod \limits _{i=1}^m\left (1+x^{e_i^G({U_M^N})}y^{e_i^N(M)}u\right )}{\prod \limits _{j=1}^r\left (1-x^{d_j^G}\right )}.$
Proof. We proceed as in the proof of Corollary 3.7: let
![]() $y_1,\dots ,y_m$
be a basis of
$y_1,\dots ,y_m$
be a basis of
![]() $M^*$
. Let
$M^*$
. Let
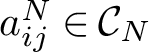 $a_{ij}^N\in {\mathcal {C}_N}$
be
$a_{ij}^N\in {\mathcal {C}_N}$
be
![]() $\mathbf {x}$
-homogeneous such that
$\mathbf {x}$
-homogeneous such that
 $u_i^N:=\sum _{j=1}^ma_{ij}^N\otimes y_j$
form a basis for the
$u_i^N:=\sum _{j=1}^ma_{ij}^N\otimes y_j$
form a basis for the
![]() $e_i^N(M)$
-homogeneous component of
$e_i^N(M)$
-homogeneous component of
![]() ${(U_M^N)^*}$
, and choose
${(U_M^N)^*}$
, and choose
![]() $\mathbf {x}$
-homogeneous
$\mathbf {x}$
-homogeneous
 $a_{ij}^H\in {\mathcal {C}_H}$
such that
$a_{ij}^H\in {\mathcal {C}_H}$
such that
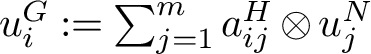 $u_i^G:=\sum _{j=1}^ma_{ij}^H\otimes u_j^N$
form a basis for
$u_i^G:=\sum _{j=1}^ma_{ij}^H\otimes u_j^N$
form a basis for
 $({\mathcal {C}_H}\otimes (U_M^N)^*_{e_i^N(M)})^H$
with
$({\mathcal {C}_H}\otimes (U_M^N)^*_{e_i^N(M)})^H$
with
![]() $\mathrm {deg}_{\mathbf {x}}(u_i^G)=e_i^G(U_M^N)$
(where again
$\mathrm {deg}_{\mathbf {x}}(u_i^G)=e_i^G(U_M^N)$
(where again
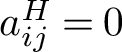 $a_{ij}^H=0$
whenever
$a_{ij}^H=0$
whenever
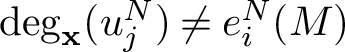 $\mathrm {deg}_{\mathbf {x}}(u_j^N)\neq e_i^N(M)$
). But then the
$\mathrm {deg}_{\mathbf {x}}(u_j^N)\neq e_i^N(M)$
). But then the
![]() $u_i^G$
form an
$u_i^G$
form an
![]() $\mathbf {x}$
-homogeneous basis for
$\mathbf {x}$
-homogeneous basis for
![]() $({\mathcal {C}_H}\otimes (U_M^N)^*)^H$
. Because
$({\mathcal {C}_H}\otimes (U_M^N)^*)^H$
. Because
![]() ${U_M^N}$
consists of N-invariants, by Lemma 3.10 we have that
${U_M^N}$
consists of N-invariants, by Lemma 3.10 we have that
![]() $({\mathcal {C}_G}\otimes {(U_M^N)^*})^G\simeq ({\mathcal {C}_H}\otimes {(U_M^N)^*})^H$
. By Proposition 3.12, because M is amenable as a G-module,
$({\mathcal {C}_G}\otimes {(U_M^N)^*})^G\simeq ({\mathcal {C}_H}\otimes {(U_M^N)^*})^H$
. By Proposition 3.12, because M is amenable as a G-module,
![]() ${U_M^N}$
is amenable. Hence, by Theorem 2.7 we have that
${U_M^N}$
is amenable. Hence, by Theorem 2.7 we have that
Because
![]() $({\mathcal {C}_G}\otimes {(U_M^N)^*})^G\simeq {\mathrm {span}}_{\mathbb {C}}\{u_1^G,\dots ,u_m^G\}$
and
$({\mathcal {C}_G}\otimes {(U_M^N)^*})^G\simeq {\mathrm {span}}_{\mathbb {C}}\{u_1^G,\dots ,u_m^G\}$
and
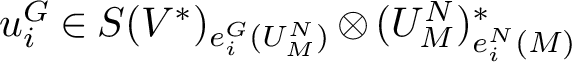 $u_i^G\in S(V^*)_{e_i^G({U_M^N})}\otimes (U_M^N)^*_{e_i^N(M)}$
, our result follows.
$u_i^G\in S(V^*)_{e_i^G({U_M^N})}\otimes (U_M^N)^*_{e_i^N(M)}$
, our result follows.
To simplify notation, for
![]() $e\in {\mathcal {E}_M^N}$
we denote by
$e\in {\mathcal {E}_M^N}$
we denote by
![]() ${(U_M^N)_e}$
the homogeneous component of
${(U_M^N)_e}$
the homogeneous component of
![]() ${U_M^N}$
corresponding to the dual of
${U_M^N}$
corresponding to the dual of
![]() ${(U_M^N)^*_e}$
, rather than the more natural but cumbersome graded dual
${(U_M^N)^*_e}$
, rather than the more natural but cumbersome graded dual
![]() $({U_M^N})_{-e}$
instead of our
$({U_M^N})_{-e}$
instead of our
![]() ${(U_M^N)_e}$
.
${(U_M^N)_e}$
.
Proposition 3.16.
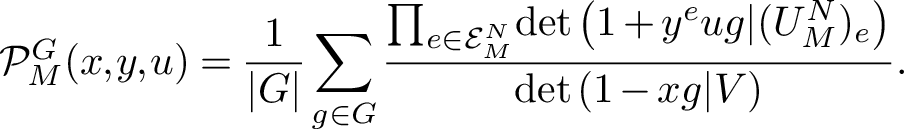 $\mathcal {P}^G_M(x,y,u)=\displaystyle \frac {1}{|G|}\sum \limits _{g\in G}\frac {{\textstyle \prod _{e\in {\mathcal {E}_M^N}}}\mathrm {det}\left (1+y^eug|({U_M^N})_e\right )}{\mathrm {det}\left (1-xg|V\right )}.$
$\mathcal {P}^G_M(x,y,u)=\displaystyle \frac {1}{|G|}\sum \limits _{g\in G}\frac {{\textstyle \prod _{e\in {\mathcal {E}_M^N}}}\mathrm {det}\left (1+y^eug|({U_M^N})_e\right )}{\mathrm {det}\left (1-xg|V\right )}.$
Proof. For
![]() $g\in G$
, let us write
$g\in G$
, let us write
 $$ \begin{align*}\mathcal{P}^g_M(x,y,u)=\sum_{\ell,e,p\geq 0}\mathrm{tr}\bigl(g|S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)x^\ell y^e u^p,\end{align*} $$
$$ \begin{align*}\mathcal{P}^g_M(x,y,u)=\sum_{\ell,e,p\geq 0}\mathrm{tr}\bigl(g|S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)x^\ell y^e u^p,\end{align*} $$
so that
 $\mathcal {P}^G_M(x,y,u)=\frac {1}{|G|}\sum _{g\in G}\mathcal {P}^g_M(x,y,u)$
and
$\mathcal {P}^G_M(x,y,u)=\frac {1}{|G|}\sum _{g\in G}\mathcal {P}^g_M(x,y,u)$
and
 $$ \begin{align*}\mathcal{P}^g_M(x,y,u)=\left(\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S(V^*)_\ell\bigr)x^\ell\right)\left(\sum_{e,p\geq 0}\mathrm{tr}\bigl(g|({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)y^eu^p\right).\end{align*} $$
$$ \begin{align*}\mathcal{P}^g_M(x,y,u)=\left(\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S(V^*)_\ell\bigr)x^\ell\right)\left(\sum_{e,p\geq 0}\mathrm{tr}\bigl(g|({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)y^eu^p\right).\end{align*} $$
We know that
 $ \sum _{\ell \geq 0}\mathrm {tr}\bigl (g|S(V^*)_\ell \bigr )x^\ell =\mathrm {det}(1-xg^{-1}|V)^{-1}$
. On the other hand, because
$ \sum _{\ell \geq 0}\mathrm {tr}\bigl (g|S(V^*)_\ell \bigr )x^\ell =\mathrm {det}(1-xg^{-1}|V)^{-1}$
. On the other hand, because
 ${(U_M^N)^*}\simeq \bigoplus _{e\in {\mathcal {E}_M^N}}{(U_M^N)^*_e}$
, we have that
${(U_M^N)^*}\simeq \bigoplus _{e\in {\mathcal {E}_M^N}}{(U_M^N)^*_e}$
, we have that
 $\bigwedge {(U_M^N)^*}\simeq \bigotimes _{e\in {\mathcal {E}_M^N}}\bigwedge {(U_M^N)^*_e}$
as bigraded G-modules. Hence, for each
$\bigwedge {(U_M^N)^*}\simeq \bigotimes _{e\in {\mathcal {E}_M^N}}\bigwedge {(U_M^N)^*_e}$
as bigraded G-modules. Hence, for each
![]() $g\in G$
,
$g\in G$
,
 $$ \begin{align*}\sum_{e,p\geq 0}\mathrm{tr}\bigl(g|({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)y^eu^p=\prod_{e\in{\mathcal{E}_M^N}}\left(\sum_{p\geq 0}\mathrm{tr}\bigl(g|{\textstyle\bigwedge^p}{(U_M^N)^*_e}\bigr)y^{ep}u^p\right).\end{align*} $$
$$ \begin{align*}\sum_{e,p\geq 0}\mathrm{tr}\bigl(g|({\textstyle\bigwedge^p}{(U_M^N)^*})_e\bigr)y^eu^p=\prod_{e\in{\mathcal{E}_M^N}}\left(\sum_{p\geq 0}\mathrm{tr}\bigl(g|{\textstyle\bigwedge^p}{(U_M^N)^*_e}\bigr)y^{ep}u^p\right).\end{align*} $$
For each
![]() $e\in {\mathcal {E}_M^N}$
we have that
$e\in {\mathcal {E}_M^N}$
we have that
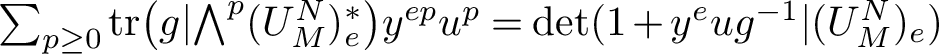 $\sum _{p\geq 0}\mathrm {tr}\bigl (g|{\textstyle \bigwedge ^p}{(U_M^N)^*_e}\bigr )y^{ep}u^p=\mathrm {det}(1+y^eug^{-1}|{(U_M^N)_e})$
. Hence, for each
$\sum _{p\geq 0}\mathrm {tr}\bigl (g|{\textstyle \bigwedge ^p}{(U_M^N)^*_e}\bigr )y^{ep}u^p=\mathrm {det}(1+y^eug^{-1}|{(U_M^N)_e})$
. Hence, for each
![]() $g\in G$
,
$g\in G$
,
 $$ \begin{align*} \mathcal{P}^g_M(x,y,u)=\frac{\prod_{e\in{\mathcal{E}_M^N}}\mathrm{det}(1+y^eug^{-1}|{(U_M^N)_e})}{\mathrm{det}(1-xg^{-1}|V)}.\end{align*} $$
$$ \begin{align*} \mathcal{P}^g_M(x,y,u)=\frac{\prod_{e\in{\mathcal{E}_M^N}}\mathrm{det}(1+y^eug^{-1}|{(U_M^N)_e})}{\mathrm{det}(1-xg^{-1}|V)}.\end{align*} $$
Our result follows after taking the average over
![]() $g\in G$
on each side.
$g\in G$
on each side.
4 Proofs of the Main Theorems
We are now in a position to apply the results of Section 3 to prove the main results announced in the Introduction. Fix
![]() $G\subset \mathrm {GL}(V)$
a complex reflection group acting by reflections on the vector space V of dimension r. Let
$G\subset \mathrm {GL}(V)$
a complex reflection group acting by reflections on the vector space V of dimension r. Let
![]() $N\trianglelefteq G$
be a normal reflection subgroup with quotient
$N\trianglelefteq G$
be a normal reflection subgroup with quotient
![]() $H=G/N$
, which acts by reflections on
$H=G/N$
, which acts by reflections on
![]() ${E}=V/N$
. For
${E}=V/N$
. For
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
, where
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
, where
![]() $\zeta _G$
denotes a primitive
$\zeta _G$
denotes a primitive
![]() $|G|$
th root of unity, write
$|G|$
th root of unity, write
![]() ${V^\sigma }$
for the Galois twist of V (as defined in Section 2.3). As in Definition 2.9, we write
${V^\sigma }$
for the Galois twist of V (as defined in Section 2.3). As in Definition 2.9, we write
![]() ${U^N}$
for the dual of
${U^N}$
for the dual of
![]() $({\mathcal {C}_N}\otimes V^*)^N$
and, more generally,
$({\mathcal {C}_N}\otimes V^*)^N$
and, more generally,
![]() ${U^N_\sigma }$
for the dual of
${U^N_\sigma }$
for the dual of
![]() $({\mathcal {C}_N}\otimes {(V^\sigma )^*})^N$
.
$({\mathcal {C}_N}\otimes {(V^\sigma )^*})^N$
.
4.1 Proof of Theorem 1.3
Theorem 1.3. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Let
$N\trianglelefteq G$
be a normal reflection subgroup. Let
![]() $H=G/N$
and
$H=G/N$
and
![]() ${E}=V/N$
. Then for a suitable choice of indexing we have
${E}=V/N$
. Then for a suitable choice of indexing we have
 $$ \begin{align*} e_i^N({V^\sigma}) {+} e_i^G({U^N_\sigma}) & = e_i^G({V^\sigma})\\ d_i^N \cdot e_i^H({E^\sigma}) & = e_i^G({E^\sigma})\\ d_i^N\cdot d_i^H & =d_i^G. \end{align*} $$
$$ \begin{align*} e_i^N({V^\sigma}) {+} e_i^G({U^N_\sigma}) & = e_i^G({V^\sigma})\\ d_i^N \cdot e_i^H({E^\sigma}) & = e_i^G({E^\sigma})\\ d_i^N\cdot d_i^H & =d_i^G. \end{align*} $$
Proof. The first equality is Corollary 3.7 applied to the G-module
![]() $M={V^\sigma }$
, and the last equality follows from the observations in Remark 3.1.
$M={V^\sigma }$
, and the last equality follows from the observations in Remark 3.1.
Let us establish the second equality. Let
![]() ${N}^\sigma _1,\dots ,{N}^\sigma _r$
denote a basis for
${N}^\sigma _1,\dots ,{N}^\sigma _r$
denote a basis for
![]() ${(E^\sigma )^*}$
as a G-module. We will show that there exist
${(E^\sigma )^*}$
as a G-module. We will show that there exist
![]() $a_{ij}\in S({E^*})$
such that
$a_{ij}\in S({E^*})$
such that
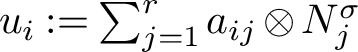 $u_i:=\sum _{j=1}^r a_{ij}\otimes {N}_j^\sigma $
form an
$u_i:=\sum _{j=1}^r a_{ij}\otimes {N}_j^\sigma $
form an
![]() $\mathbf {N}$
-homogeneous basis for
$\mathbf {N}$
-homogeneous basis for
![]() $({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
(so that each nonzero
$({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
(so that each nonzero
![]() $a_{ij}$
is
$a_{ij}$
is
![]() $\mathbf {N}$
-homogeneous of
$\mathbf {N}$
-homogeneous of
![]() $\mathbf {N}$
-degree
$\mathbf {N}$
-degree
![]() $e_i^H({E^\sigma })$
) and, moreover,
$e_i^H({E^\sigma })$
) and, moreover,
![]() $a_{ij}=0$
whenever
$a_{ij}=0$
whenever
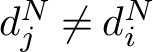 $d_j^N\neq d_i^N$
and each
$d_j^N\neq d_i^N$
and each
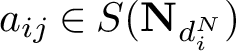 $a_{ij}\in S(\mathbf {N}_{d_i^N})$
, where as before
$a_{ij}\in S(\mathbf {N}_{d_i^N})$
, where as before
![]() $\mathbf {N}_d$
denotes the set of fundamental N-invariants of degree d. Because
$\mathbf {N}_d$
denotes the set of fundamental N-invariants of degree d. Because
![]() $({\mathcal {C}_G}\otimes {(E^\sigma )^*})^G\simeq ({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
by Lemma 3.10, the existence of such
$({\mathcal {C}_G}\otimes {(E^\sigma )^*})^G\simeq ({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
by Lemma 3.10, the existence of such
![]() $a_{ij}$
will establish our claim, because each nonzero
$a_{ij}$
will establish our claim, because each nonzero
![]() $a_{ij}$
as above will then be
$a_{ij}$
as above will then be
![]() $\mathbf {x}$
-homogeneous of
$\mathbf {x}$
-homogeneous of
![]() $\mathbf {x}$
-degree
$\mathbf {x}$
-degree
![]() $e_i^G({E^\sigma })= d_i^N\cdot e_i^H({E^\sigma })$
.
$e_i^G({E^\sigma })= d_i^N\cdot e_i^H({E^\sigma })$
.
As in Remark 3.1, let us write
![]() ${\mathcal {D}_N}=\{d_1^N,\dots ,d_r^N\}$
for the set of degrees of N and
${\mathcal {D}_N}=\{d_1^N,\dots ,d_r^N\}$
for the set of degrees of N and
![]() ${E^*_d}$
for the graded component of
${E^*_d}$
for the graded component of
![]() ${E^*}$
spanned by the fundamental N-invariants of degree
${E^*}$
spanned by the fundamental N-invariants of degree
![]() $d\in {\mathcal {D}_N}$
. To simplify notation, let us write
$d\in {\mathcal {D}_N}$
. To simplify notation, let us write
![]() ${E}_d$
for the graded dual of
${E}_d$
for the graded dual of
![]() ${E^*_d}$
, instead of
${E^*_d}$
, instead of
![]() ${E}_{-d}$
, so that
${E}_{-d}$
, so that
![]() ${E}\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E}_d$
, and similarly the Galois twist
${E}\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E}_d$
, and similarly the Galois twist
![]() ${E^\sigma }\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E}^\sigma _d$
. We saw in Remark 3.1 that H decomposes as a direct product
${E^\sigma }\simeq \bigoplus _{d\in {\mathcal {D}_N}}{E}^\sigma _d$
. We saw in Remark 3.1 that H decomposes as a direct product
![]() $\unicode{x2A09} _{d\in {\mathcal {D}_N}}H_{(d)}$
, where each
$\unicode{x2A09} _{d\in {\mathcal {D}_N}}H_{(d)}$
, where each
![]() $H_{(d)}$
is a reflection group acting on
$H_{(d)}$
is a reflection group acting on
![]() ${E}_d$
and
${E}_d$
and
![]() $H_{(d)}$
acts trivially on
$H_{(d)}$
acts trivially on
![]() ${E}^\sigma _{d'}$
whenever
${E}^\sigma _{d'}$
whenever
![]() $d\neq d'$
. We then see that
$d\neq d'$
. We then see that
![]() $S({E^*})\simeq \bigotimes _{d\in {\mathcal {D}_N}} S({E^*_d})$
and each
$S({E^*})\simeq \bigotimes _{d\in {\mathcal {D}_N}} S({E^*_d})$
and each
 $S({E^*_d})\simeq S({E^*_d})^{H_{(d)}}\otimes \mathcal {C}_{H_{(d)}}$
as H-modules, so that in particular
$S({E^*_d})\simeq S({E^*_d})^{H_{(d)}}\otimes \mathcal {C}_{H_{(d)}}$
as H-modules, so that in particular
![]() ${\mathcal {C}_H}\simeq \bigotimes _{d\in {\mathcal {D}_N}}\mathcal {C}_{H_{(d)}}$
as H-modules, where again
${\mathcal {C}_H}\simeq \bigotimes _{d\in {\mathcal {D}_N}}\mathcal {C}_{H_{(d)}}$
as H-modules, where again
![]() $H_{(d)}$
acts trivially on
$H_{(d)}$
acts trivially on
![]() $\mathcal {C}_{H_{(d')}}$
for
$\mathcal {C}_{H_{(d')}}$
for
![]() $d\neq d'$
. It follows from the above observations that
$d\neq d'$
. It follows from the above observations that

so that we may indeed choose
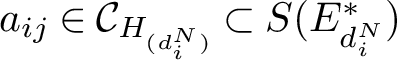 $a_{ij}\in \mathcal {C}_{H_{(d_i^N)}}\subset S({E}_{d_i^N}^*)$
such that the
$a_{ij}\in \mathcal {C}_{H_{(d_i^N)}}\subset S({E}_{d_i^N}^*)$
such that the
![]() $\mathbf {N}$
-homogeneous
$\mathbf {N}$
-homogeneous
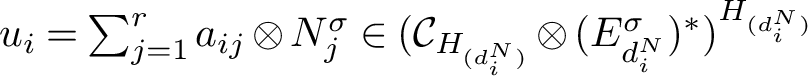 $u_i=\sum _{j=1}^ra_{ij}\otimes {N}_j^\sigma \in (\mathcal {C}_{H_{(d_i^N)}}\otimes ({E}^\sigma _{d_i^N})^*)^{H_{(d_i^N)}}$
(i.e., with
$u_i=\sum _{j=1}^ra_{ij}\otimes {N}_j^\sigma \in (\mathcal {C}_{H_{(d_i^N)}}\otimes ({E}^\sigma _{d_i^N})^*)^{H_{(d_i^N)}}$
(i.e., with
![]() $a_{ij}=0$
whenever
$a_{ij}=0$
whenever
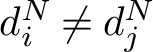 $d_i^N\neq d_j^N$
) form a basis for
$d_i^N\neq d_j^N$
) form a basis for
![]() $({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
that is simultaneously
$({\mathcal {C}_H}\otimes {(E^\sigma )^*})^H$
that is simultaneously
![]() $\mathbf {N}$
-homogeneous of
$\mathbf {N}$
-homogeneous of
![]() $\mathbf {N}$
-degree
$\mathbf {N}$
-degree
![]() $e_i^H({E^\sigma })$
and
$e_i^H({E^\sigma })$
and
![]() $\mathbf {x}$
-homogeneous of
$\mathbf {x}$
-homogeneous of
![]() $\mathbf {x}$
-degree
$\mathbf {x}$
-degree
![]() $e_i^G({E^\sigma })=d_i^N\cdot e_i^H({E^\sigma })$
.
$e_i^G({E^\sigma })=d_i^N\cdot e_i^H({E^\sigma })$
.
When
![]() $\sigma =1$
, the G-module
$\sigma =1$
, the G-module
![]() ${U^N_\sigma }$
in Definition 2.9 admits a more concrete description.
${U^N_\sigma }$
in Definition 2.9 admits a more concrete description.
Lemma 4.1 [Reference Bonnafé, Lehrer and Michel7, Example 2.4]
Let
![]() $\eta :S(V^*)\rightarrow {\mathcal {C}_N}$
denote the projection onto the space of N-harmonic polynomials, and let
$\eta :S(V^*)\rightarrow {\mathcal {C}_N}$
denote the projection onto the space of N-harmonic polynomials, and let
 $$ \begin{align*} d:{E}^*={\mathrm{span}}_{\mathbb{C}}\{{N}_1,\dots,{N}_r\}&\to {\mathrm{span}}_{\mathbb{C}}\{d{N}_1,\dots,d{N}_r\}\\ {N}_i&\mapsto d{N}_i=\sum_{j=1}^r\frac{\partial {N}_i}{\partial x_j}\otimes x_j.\end{align*} $$
$$ \begin{align*} d:{E}^*={\mathrm{span}}_{\mathbb{C}}\{{N}_1,\dots,{N}_r\}&\to {\mathrm{span}}_{\mathbb{C}}\{d{N}_1,\dots,d{N}_r\}\\ {N}_i&\mapsto d{N}_i=\sum_{j=1}^r\frac{\partial {N}_i}{\partial x_j}\otimes x_j.\end{align*} $$
Then
![]() $(\eta \otimes 1)\circ d:{E^*}\rightarrow {(U^N)^*}$
is a graded (of degree
$(\eta \otimes 1)\circ d:{E^*}\rightarrow {(U^N)^*}$
is a graded (of degree
![]() $-1$
) isomorphism of G-modules.
$-1$
) isomorphism of G-modules.
Remark 4.2. As mentioned in the Introduction, in the case where
![]() $\sigma =1$
, once we replace
$\sigma =1$
, once we replace
![]() $e_i^G({U^N})=e_i^G({E})$
by Lemma 4.1, the equalities in Theorem 1.3 are compatible with the classical relations
$e_i^G({U^N})=e_i^G({E})$
by Lemma 4.1, the equalities in Theorem 1.3 are compatible with the classical relations
![]() $d_i^G=e_i^G(V)+1$
,
$d_i^G=e_i^G(V)+1$
,
![]() $d_i^N=e_i^N(V)+1$
and
$d_i^N=e_i^N(V)+1$
and
![]() $d_i^H=e_i^H({E})+1$
. To see this, we proceed as in [Reference Arreche and Williams1, Theorem 1.3]. We found in Remark 3.1 a choice of
$d_i^H=e_i^H({E})+1$
. To see this, we proceed as in [Reference Arreche and Williams1, Theorem 1.3]. We found in Remark 3.1 a choice of
![]() $\mathbf {N}$
-homogeneous H-invariants
$\mathbf {N}$
-homogeneous H-invariants
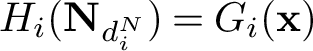 ${H}_i(\mathbf {N}_{d_i^N})={G}_i(\mathbf {x})$
, a set of fundamental G-invariants as in Equation (5), immediately resulting in the equality
${H}_i(\mathbf {N}_{d_i^N})={G}_i(\mathbf {x})$
, a set of fundamental G-invariants as in Equation (5), immediately resulting in the equality
![]() $d_i^N\cdot d_i^H=d_i^G$
of Theorem 1.3. Let us show that this same choice of indexing results in the other two equalities of Theorem 1.3. We begin by comparing
$d_i^N\cdot d_i^H=d_i^G$
of Theorem 1.3. Let us show that this same choice of indexing results in the other two equalities of Theorem 1.3. We begin by comparing
![]() $\mathbf {x}$
-degrees in
$\mathbf {x}$
-degrees in
 $$ \begin{align*}d{G}_i=\sum_{j=1}^r\frac{\partial{G}_i}{\partial x_j}\otimes x_j=\sum_{k=1}^r\frac{\partial {H}_i}{\partial {N}_k}\cdot d{N}_k=\sum_{k=1}^r\sum_{j=1}^r\frac{\partial {H}_i}{\partial {N}_k}\cdot\frac{\partial{N}_k}{\partial x_j}\otimes x_j.\end{align*} $$
$$ \begin{align*}d{G}_i=\sum_{j=1}^r\frac{\partial{G}_i}{\partial x_j}\otimes x_j=\sum_{k=1}^r\frac{\partial {H}_i}{\partial {N}_k}\cdot d{N}_k=\sum_{k=1}^r\sum_{j=1}^r\frac{\partial {H}_i}{\partial {N}_k}\cdot\frac{\partial{N}_k}{\partial x_j}\otimes x_j.\end{align*} $$
Recall that
![]() $e_i^G(V)=d_i^G-1=\mathrm {deg}_{\mathbf {x}}(d{G}_i)$
and
$e_i^G(V)=d_i^G-1=\mathrm {deg}_{\mathbf {x}}(d{G}_i)$
and
![]() $e_i^N(V)=d_i^N-1=\mathrm {deg}_{\mathbf {x}}(d{N}_i)$
. Similarly,
$e_i^N(V)=d_i^N-1=\mathrm {deg}_{\mathbf {x}}(d{N}_i)$
. Similarly,
![]() $e_i^H(E)=d_i^H-1=\mathrm {deg}_{\mathbf {N}}(d{H}_i)$
, where now
$e_i^H(E)=d_i^H-1=\mathrm {deg}_{\mathbf {N}}(d{H}_i)$
, where now
 $d{H}_i=\sum _{k=1}^r\frac {\partial {H}_i}{\partial {N}_k}\otimes {N}_k\in (S({E^*})\otimes {E^*})^H$
. Because
$d{H}_i=\sum _{k=1}^r\frac {\partial {H}_i}{\partial {N}_k}\otimes {N}_k\in (S({E^*})\otimes {E^*})^H$
. Because
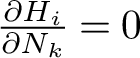 $\frac {\partial {H}_i}{\partial {N}_k}=0$
whenever
$\frac {\partial {H}_i}{\partial {N}_k}=0$
whenever
![]() $\mathrm {deg}_{\mathbf {x}}({N}_k)\neq d_i^N$
, it follows that
$\mathrm {deg}_{\mathbf {x}}({N}_k)\neq d_i^N$
, it follows that
It remains to show that
![]() $d_i^N\cdot e_i^H(E)=e_i^G({E})$
under this same choice of indexing.
$d_i^N\cdot e_i^H(E)=e_i^G({E})$
under this same choice of indexing.
The
![]() $e_i^G({E})$
are the
$e_i^G({E})$
are the
![]() $\mathbf {x}$
-degrees of a homogeneous basis for
$\mathbf {x}$
-degrees of a homogeneous basis for
![]() $({\mathcal {C}_G}\otimes {E^*})^G$
. By Lemma 3.10,
$({\mathcal {C}_G}\otimes {E^*})^G$
. By Lemma 3.10,
![]() $({\mathcal {C}_G}\otimes {E^*})^G\simeq ({\mathcal {C}_H}\otimes {E^*})^H$
, and therefore the
$({\mathcal {C}_G}\otimes {E^*})^G\simeq ({\mathcal {C}_H}\otimes {E^*})^H$
, and therefore the
![]() $(\eta _H\otimes 1)(d{H}_i)$
serve as a homogeneous basis for
$(\eta _H\otimes 1)(d{H}_i)$
serve as a homogeneous basis for
![]() $({\mathcal {C}_G}\otimes {E^*})^G$
, where
$({\mathcal {C}_G}\otimes {E^*})^G$
, where
![]() $\eta _H:S({E^*})\rightarrow {\mathcal {C}_H}$
denotes the projection onto the space of H-harmonic polynomials (cf. Lemma 4.1). Hence, for any k such that
$\eta _H:S({E^*})\rightarrow {\mathcal {C}_H}$
denotes the projection onto the space of H-harmonic polynomials (cf. Lemma 4.1). Hence, for any k such that
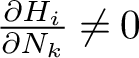 $\frac {\partial {H}_i}{\partial {N}_k}\neq 0$
, the
$\frac {\partial {H}_i}{\partial {N}_k}\neq 0$
, the
![]() $e_i^G({E})$
are given by
$e_i^G({E})$
are given by
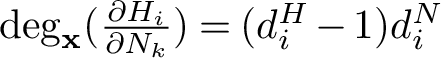 $\mathrm {deg}_{\mathbf {x}}(\frac {\partial {H}_i}{\partial {N}_k})=(d_i^H-1)d_i^N$
.
$\mathrm {deg}_{\mathbf {x}}(\frac {\partial {H}_i}{\partial {N}_k})=(d_i^H-1)d_i^N$
.
The proof of the second equality of Theorem 1.3 generalises what is essential in the case
![]() $\sigma =1$
– where we have explicit bases for the relevant Orlik-Solomon spaces of Definition 2.9 in terms of fundamental invariants (up to a harmless isomorphism as in Lemma 4.1):
$\sigma =1$
– where we have explicit bases for the relevant Orlik-Solomon spaces of Definition 2.9 in terms of fundamental invariants (up to a harmless isomorphism as in Lemma 4.1):
![]() $\{d{G}_i\}$
for
$\{d{G}_i\}$
for
![]() ${(U^G)^*}$
,
${(U^G)^*}$
,
![]() $\{d{N}_i\}$
for
$\{d{N}_i\}$
for
![]() ${(U^N)^*}$
and
${(U^N)^*}$
and
![]() $\{d{H}_i\}$
for
$\{d{H}_i\}$
for
![]() $(U^H)^*$
– to the more general situation where
$(U^H)^*$
– to the more general situation where
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
is arbitrary.
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
is arbitrary.
Example 4.3. Take
![]() $G=W(F_4)=G_{28}$
, N to be the normal subgroup generated by the reflections corresponding to short roots (see the proof of Theorem 6.2 for more details), and
$G=W(F_4)=G_{28}$
, N to be the normal subgroup generated by the reflections corresponding to short roots (see the proof of Theorem 6.2 for more details), and
![]() $\sigma =1$
. Then
$\sigma =1$
. Then
![]() $N\simeq W(D_4)$
and
$N\simeq W(D_4)$
and
![]() $G/N\simeq W(A_2)=\mathfrak {S}_3$
acts by reflections on
$G/N\simeq W(A_2)=\mathfrak {S}_3$
acts by reflections on
![]() $\mathbb {C} \oplus \mathbb {C} \oplus \mathbb {C}^2$
(trivially on
$\mathbb {C} \oplus \mathbb {C} \oplus \mathbb {C}^2$
(trivially on
![]() $\mathbb {C}\oplus \mathbb {C}$
). Theorem 1.3 corresponds to the identities
$\mathbb {C}\oplus \mathbb {C}$
). Theorem 1.3 corresponds to the identities
 $$ \begin{align*} (1,5,3,3) {+} (0,0,4,8) &= (1,5,7,11) \\ (2,6,4,4) \cdot (0,0,1,2) & = (0,0,4,8)\\ (2,6,4,4) \cdot (1,1,2,3) & = (2,6,8,12). \end{align*} $$
$$ \begin{align*} (1,5,3,3) {+} (0,0,4,8) &= (1,5,7,11) \\ (2,6,4,4) \cdot (0,0,1,2) & = (0,0,4,8)\\ (2,6,4,4) \cdot (1,1,2,3) & = (2,6,8,12). \end{align*} $$
Note that the exponents and degrees of
![]() $N \simeq W(D_4)$
must be reordered for the identities to hold (see Remark 3.1).
$N \simeq W(D_4)$
must be reordered for the identities to hold (see Remark 3.1).
Remark 4.4. When
![]() $\sigma =1$
,
$\sigma =1$
,
![]() ${U^N_\sigma } \simeq {E^\sigma }$
as G-representations by Lemma 4.1 – but it is not always the case that
${U^N_\sigma } \simeq {E^\sigma }$
as G-representations by Lemma 4.1 – but it is not always the case that
![]() ${U^N_\sigma } \simeq {E^\sigma }$
as G-representations for more general
${U^N_\sigma } \simeq {E^\sigma }$
as G-representations for more general
![]() $\sigma $
. For example, take the cyclic groups
$\sigma $
. For example, take the cyclic groups
![]() $G=C_a \triangleright C_d=N$
for
$G=C_a \triangleright C_d=N$
for
![]() $d|a$
, with
$d|a$
, with
![]() $\sigma $
being complex conjugation. Then
$\sigma $
being complex conjugation. Then
![]() ${(U^N_\sigma )^*} = {\mathrm {span}}_{\mathbb {C}}\{ x \otimes x^\sigma \}$
, on which G acts trivially. We discuss this in more detail in Section 7.1. See Section 7 for more examples of explicit identifications of the spaces
${(U^N_\sigma )^*} = {\mathrm {span}}_{\mathbb {C}}\{ x \otimes x^\sigma \}$
, on which G acts trivially. We discuss this in more detail in Section 7.1. See Section 7 for more examples of explicit identifications of the spaces
![]() ${U^N_\sigma }$
.
${U^N_\sigma }$
.
4.2 Proof of Theorem 1.4
Theorem 1.4. Let
![]() $G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
$G\subset \mathrm {GL}(V)$
be a complex reflection group of rank r and let
![]() $N\trianglelefteq G$
be a normal reflection subgroup. Let
$N\trianglelefteq G$
be a normal reflection subgroup. Let
![]() ${E}=V/N$
and
${E}=V/N$
and
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then for a suitable choice of indexing we have
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
. Then for a suitable choice of indexing we have
 $$ \begin{align*}\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)} = \prod_{i=1}^r \left(qt+e_i^N(V^\sigma) t + e_i^G({U^N_\sigma})\right),\end{align*} $$
$$ \begin{align*}\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)} = \prod_{i=1}^r \left(qt+e_i^N(V^\sigma) t + e_i^G({U^N_\sigma})\right),\end{align*} $$
where the
![]() $\lambda _i(g)$
are the eigenvalues of
$\lambda _i(g)$
are the eigenvalues of
![]() $g\in G$
acting on V.
$g\in G$
acting on V.
We refer to the left-hand side of Theorem 1.4 as the sum side and to the right-hand side as the product side. We will prove Theorem 1.4 by computing the limit as
![]() $x \to 1$
of the specialisation
$x \to 1$
of the specialisation
![]() $y\mapsto x^t$
and
$y\mapsto x^t$
and
![]() $u\mapsto qt(1-x)-1$
of the trigraded Poincaré series
$u\mapsto qt(1-x)-1$
of the trigraded Poincaré series
![]() $\mathcal {P}^G_\sigma (x,y,u):=\mathcal {P}^G_{{V^\sigma }}(x,y,u)$
from Definition 3.14 in two different ways to obtain the sum side and the product side separately.
$\mathcal {P}^G_\sigma (x,y,u):=\mathcal {P}^G_{{V^\sigma }}(x,y,u)$
from Definition 3.14 in two different ways to obtain the sum side and the product side separately.
Proof Proof of Theorem 1.4
By Corollaries 4.5 and 4.11, both sides are equal to
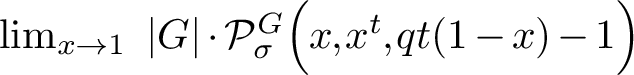 $\lim _{x\to 1} \ |G|\cdot \mathcal {P}^G_{\sigma }\Bigl (x,x^t,qt(1-x)-1\Bigr )$
.
$\lim _{x\to 1} \ |G|\cdot \mathcal {P}^G_{\sigma }\Bigl (x,x^t,qt(1-x)-1\Bigr )$
.
Because
![]() $M={V^\sigma }$
is amenable as a G-module (and as an N-module) by [Reference Orlik and Solomon16, Thm. 2.13], we can apply both Propositions 3.15 and 3.16 in this case to obtain
$M={V^\sigma }$
is amenable as a G-module (and as an N-module) by [Reference Orlik and Solomon16, Thm. 2.13], we can apply both Propositions 3.15 and 3.16 in this case to obtain
 $$ \begin{align*}\displaystyle\frac{1}{|G|}\sum\limits_{g\in G}\frac{{\textstyle\prod_{e\in{\mathcal{E}^N_\sigma}}}\mathrm{det}\left(1+y^eug|({U^N_\sigma})_e\right)}{\mathrm{det}\left(1-xg|V\right)}=\mathcal{P}^G_\sigma(x,y,u)=\prod_{i=1}^r\displaystyle\frac{\left(1+x^{e_i^G({U^N_\sigma})}y^{e_i^N({V^\sigma})}u\right)}{\left(1-x^{d_i^G}\right)},\end{align*} $$
$$ \begin{align*}\displaystyle\frac{1}{|G|}\sum\limits_{g\in G}\frac{{\textstyle\prod_{e\in{\mathcal{E}^N_\sigma}}}\mathrm{det}\left(1+y^eug|({U^N_\sigma})_e\right)}{\mathrm{det}\left(1-xg|V\right)}=\mathcal{P}^G_\sigma(x,y,u)=\prod_{i=1}^r\displaystyle\frac{\left(1+x^{e_i^G({U^N_\sigma})}y^{e_i^N({V^\sigma})}u\right)}{\left(1-x^{d_i^G}\right)},\end{align*} $$
where
![]() ${\mathcal {E}^N_\sigma }:=\{e_1^N({V^\sigma }),\dots ,e_r^N({V^\sigma })\}$
denotes the set of
${\mathcal {E}^N_\sigma }:=\{e_1^N({V^\sigma }),\dots ,e_r^N({V^\sigma })\}$
denotes the set of
![]() ${V^\sigma }$
-exponents of N as before. The product side of Theorem 1.4 follows immediately.
${V^\sigma }$
-exponents of N as before. The product side of Theorem 1.4 follows immediately.
Corollary 4.5 Product side specialisation
 $$ \begin{align*}\lim_{x\to 1} \ |G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\prod_{i=1}^r \left(qt+e_i^N({V^\sigma}) t + e_i^G({U^N_\sigma})\right).\end{align*} $$
$$ \begin{align*}\lim_{x\to 1} \ |G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\prod_{i=1}^r \left(qt+e_i^N({V^\sigma}) t + e_i^G({U^N_\sigma})\right).\end{align*} $$
Proof. We compute:
 $$ \begin{align*} &|G|\prod_{i=1}^r\frac{1+x^{e_i^G({U^N_\sigma}) }y^{e_i^N({V^\sigma})}u}{1-x^{d_i^G}}\Bigg|_{\substack{y=x^t \\ u=qt(1-x)-1\\ x\to 1}} \\&= |G|\lim_{x \to 1} \prod_{i=1}^r \left(\frac{x^{e_i^G({U^N_\sigma})+t e_i^N({V^\sigma}) }qt(1-x)}{1-x^{d_i^G}}+\frac{1-x^{e_i^G({U^N_\sigma})+t e_i^N({V^\sigma})}}{1-x^{d_i^G}}\right)\\ &=\prod_{i=1}^r \left(qt+e_i^N({V^\sigma}) t + e_i^G({U^N_\sigma})\right).\\[-44pt] \end{align*} $$
$$ \begin{align*} &|G|\prod_{i=1}^r\frac{1+x^{e_i^G({U^N_\sigma}) }y^{e_i^N({V^\sigma})}u}{1-x^{d_i^G}}\Bigg|_{\substack{y=x^t \\ u=qt(1-x)-1\\ x\to 1}} \\&= |G|\lim_{x \to 1} \prod_{i=1}^r \left(\frac{x^{e_i^G({U^N_\sigma})+t e_i^N({V^\sigma}) }qt(1-x)}{1-x^{d_i^G}}+\frac{1-x^{e_i^G({U^N_\sigma})+t e_i^N({V^\sigma})}}{1-x^{d_i^G}}\right)\\ &=\prod_{i=1}^r \left(qt+e_i^N({V^\sigma}) t + e_i^G({U^N_\sigma})\right).\\[-44pt] \end{align*} $$
Our argument for the sum side of Theorem 1.4 is more delicate. The reason for this is that for
![]() $g\in G$
the fixed space of g acting on
$g\in G$
the fixed space of g acting on
![]() ${U^N_\sigma }$
often has larger dimension than the fixed space of g acting on
${U^N_\sigma }$
often has larger dimension than the fixed space of g acting on
![]() ${V^\sigma }$
, which causes many terms in the term-by-term limit to be zero.
${V^\sigma }$
, which causes many terms in the term-by-term limit to be zero.
It turns out, as we will now show, that the contributions are correct when taken coset by coset. For this, let us define for each coset
![]() $Ng\in H=G/N$
the twisted Poincaré series
$Ng\in H=G/N$
the twisted Poincaré series
 $$ \begin{align*}\mathcal{P}^{Ng}_\sigma(x,y,u):=\frac{1}{|N|}\sum_{\substack{n\in N \\ \ell,e,p\geq 0}}\mathrm{tr}(ng|(S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U^N_\sigma)^*})_e))x^\ell y^eu^p,\end{align*} $$
$$ \begin{align*}\mathcal{P}^{Ng}_\sigma(x,y,u):=\frac{1}{|N|}\sum_{\substack{n\in N \\ \ell,e,p\geq 0}}\mathrm{tr}(ng|(S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U^N_\sigma)^*})_e))x^\ell y^eu^p,\end{align*} $$
so that
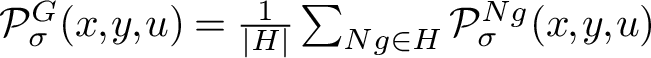 $\mathcal {P}^G_\sigma (x,y,u)=\frac {1}{|H|}\sum _{Ng\in H}\mathcal {P}^{Ng}_\sigma (x,y,u)$
. The following result is proved along the same lines as Proposition 3.16 and serves as an equivalent definition of
$\mathcal {P}^G_\sigma (x,y,u)=\frac {1}{|H|}\sum _{Ng\in H}\mathcal {P}^{Ng}_\sigma (x,y,u)$
. The following result is proved along the same lines as Proposition 3.16 and serves as an equivalent definition of
![]() $\mathcal {P}^{Ng}_\sigma (x,y,u)$
.
$\mathcal {P}^{Ng}_\sigma (x,y,u)$
.
Lemma 4.6.
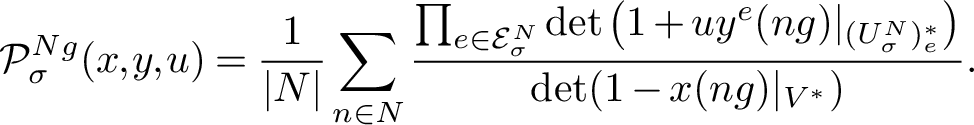 $\displaystyle \mathcal {P}^{Ng}_\sigma (x,y,u)=\frac {1}{|N|}\sum _{n \in N} \frac {\prod _{e\in {\mathcal {E}^N_\sigma }} \det \left (1+u y^{e} (ng)|_{{(U^N_\sigma )^*_e}}\right ) }{\det (1-x(ng)|_{{V^*}})}.$
$\displaystyle \mathcal {P}^{Ng}_\sigma (x,y,u)=\frac {1}{|N|}\sum _{n \in N} \frac {\prod _{e\in {\mathcal {E}^N_\sigma }} \det \left (1+u y^{e} (ng)|_{{(U^N_\sigma )^*_e}}\right ) }{\det (1-x(ng)|_{{V^*}})}.$
Proof. For each
![]() $n\in N$
,
$n\in N$
,
 $$ \begin{align*}&\sum_{\ell,e,p\geq 0}\mathrm{tr}(ng|(S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U^N_\sigma)^*})_e))x^\ell y^eu^p\\&\qquad\qquad\qquad =\left(\sum_{\ell\geq 0}\mathrm{tr}(ng|S(V^*)_\ell)x^\ell\right)\cdot\prod_{e\in{\mathcal{E}^N_\sigma}}\left(\sum_{p\geq 0}\mathrm{tr}(ng|{\textstyle\bigwedge^p}{(U^N_\sigma)^*_e})y^{ep}u^p\right),\end{align*} $$
$$ \begin{align*}&\sum_{\ell,e,p\geq 0}\mathrm{tr}(ng|(S(V^*)_\ell\otimes({\textstyle\bigwedge^p}{(U^N_\sigma)^*})_e))x^\ell y^eu^p\\&\qquad\qquad\qquad =\left(\sum_{\ell\geq 0}\mathrm{tr}(ng|S(V^*)_\ell)x^\ell\right)\cdot\prod_{e\in{\mathcal{E}^N_\sigma}}\left(\sum_{p\geq 0}\mathrm{tr}(ng|{\textstyle\bigwedge^p}{(U^N_\sigma)^*_e})y^{ep}u^p\right),\end{align*} $$
and our result follows after taking the average over
![]() $n\in N$
.
$n\in N$
.
Definition 4.7. We will adopt the following notation for the rest of this section. Let
![]() $g\in G$
. We will denote by
$g\in G$
. We will denote by
![]() $\bar {\lambda }_1(g),\dots ,\bar {\lambda }_r(g)$
the set of eigenvalues of g on
$\bar {\lambda }_1(g),\dots ,\bar {\lambda }_r(g)$
the set of eigenvalues of g on
![]() ${V^*}$
. We choose once and for all: a g-eigenbasis of fundamental N-invariants
${V^*}$
. We choose once and for all: a g-eigenbasis of fundamental N-invariants
![]() ${N}_i\in {E^*}$
such that
${N}_i\in {E^*}$
such that
![]() $\mathrm {deg}_{\mathbf {x}}({N}_i)=d_i^N$
and
$\mathrm {deg}_{\mathbf {x}}({N}_i)=d_i^N$
and
![]() $g{N}_i=\epsilon _i^g({E}){N}_i$
and a g-eigenbasis for the Orlik-Solomon space (see Definition 2.9)
$g{N}_i=\epsilon _i^g({E}){N}_i$
and a g-eigenbasis for the Orlik-Solomon space (see Definition 2.9)
![]() $u_i^N\in {(U^N_\sigma )^*}$
such that
$u_i^N\in {(U^N_\sigma )^*}$
such that
![]() $\mathrm {deg}_{\mathbf {x}}(u_i^N)=e_i^N({V^\sigma })$
and
$\mathrm {deg}_{\mathbf {x}}(u_i^N)=e_i^N({V^\sigma })$
and
![]() $gu_i^N=\epsilon _i^g({U^N_\sigma })u_i^N$
. We observe as in [Reference Bonnafé, Lehrer and Michel7] that the multisets of pairs
$gu_i^N=\epsilon _i^g({U^N_\sigma })u_i^N$
. We observe as in [Reference Bonnafé, Lehrer and Michel7] that the multisets of pairs
 $$ \begin{align*}\left\{\Bigl(\epsilon_i^g(E),d_i^N\Bigr) \ \middle| \ i=1,\dots,r\right\}\qquad\text{and} \qquad\left\{\Bigl(\epsilon_i^g({U^N_\sigma}),e_i^N({V^\sigma})\Bigr) \ \middle| \ i=1,\dots, r\right\}\end{align*} $$
$$ \begin{align*}\left\{\Bigl(\epsilon_i^g(E),d_i^N\Bigr) \ \middle| \ i=1,\dots,r\right\}\qquad\text{and} \qquad\left\{\Bigl(\epsilon_i^g({U^N_\sigma}),e_i^N({V^\sigma})\Bigr) \ \middle| \ i=1,\dots, r\right\}\end{align*} $$
depend only on
![]() $\sigma $
and the coset
$\sigma $
and the coset
![]() $Ng\in H$
and not on the choice of coset representative
$Ng\in H$
and not on the choice of coset representative
![]() $g\in Ng$
.
$g\in Ng$
.
Proposition 4.8.
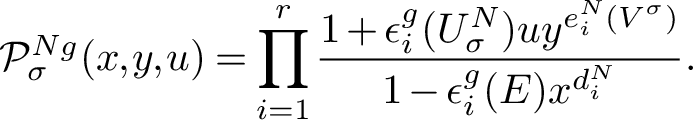 $\mathcal {P}^{Ng}_\sigma (x,y,u) = \displaystyle \prod _{i=1}^r \frac {1+ \epsilon _i^g({U^N_\sigma }) u y^{e_i^N({V^\sigma })}}{1-\epsilon _i^g({E}) x^{d_i^N}}.$
$\mathcal {P}^{Ng}_\sigma (x,y,u) = \displaystyle \prod _{i=1}^r \frac {1+ \epsilon _i^g({U^N_\sigma }) u y^{e_i^N({V^\sigma })}}{1-\epsilon _i^g({E}) x^{d_i^N}}.$
Proof. We write
![]() $\mathcal {P}^{Ng}_\sigma (x,y,u)$
as in Lemma 4.6. First observe that, because
$\mathcal {P}^{Ng}_\sigma (x,y,u)$
as in Lemma 4.6. First observe that, because
![]() ${U^N_\sigma }$
is N-invariant, for any
${U^N_\sigma }$
is N-invariant, for any
![]() $n\in N$
we have that
$n\in N$
we have that
 $$ \begin{align*}\prod_{e\in{\mathcal{E}^N_\sigma}}\mathrm{det}(1+uy^{e}(ng|_{{(U^N_\sigma)^*_e}}))=\prod_{i=1}^r(1+\epsilon_i^g({U^N_\sigma})uy^{e_i^N({V^\sigma})}),\end{align*} $$
$$ \begin{align*}\prod_{e\in{\mathcal{E}^N_\sigma}}\mathrm{det}(1+uy^{e}(ng|_{{(U^N_\sigma)^*_e}}))=\prod_{i=1}^r(1+\epsilon_i^g({U^N_\sigma})uy^{e_i^N({V^\sigma})}),\end{align*} $$
independently of
![]() $n\in N$
.
$n\in N$
.
Let
![]() $\mathcal {D}_N=\{d_1^N,\dots ,d_r^N\}$
denote the set of degrees for N, and let
$\mathcal {D}_N=\{d_1^N,\dots ,d_r^N\}$
denote the set of degrees for N, and let
![]() ${E}^*_d={\mathrm {span}}_{\mathbb {C}}\mathbf {N}_d$
for
${E}^*_d={\mathrm {span}}_{\mathbb {C}}\mathbf {N}_d$
for
![]() $d\in \mathcal {D}_N$
, where as before
$d\in \mathcal {D}_N$
, where as before
![]() $\mathbf {N}_d$
denotes the set of fundamental N-invariants having degree d. Because
$\mathbf {N}_d$
denotes the set of fundamental N-invariants having degree d. Because
![]() $S({E}^*)\simeq \bigotimes _{d\in \mathcal {D}_N}S({E}^*_d),$
we have that
$S({E}^*)\simeq \bigotimes _{d\in \mathcal {D}_N}S({E}^*_d),$
we have that
 $$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell = \prod_{d\in\mathcal{D}_N}\Bigl(\sum_{\ell\geq 0}\bigl(\mathrm{tr}(g|\mathrm{Sym}^\ell({E}^*_d))(x^{d})^\ell\bigr)\Bigr), \end{align*} $$
$$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell = \prod_{d\in\mathcal{D}_N}\Bigl(\sum_{\ell\geq 0}\bigl(\mathrm{tr}(g|\mathrm{Sym}^\ell({E}^*_d))(x^{d})^\ell\bigr)\Bigr), \end{align*} $$
where
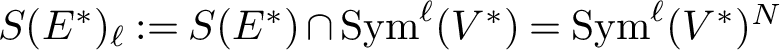 $S({E}^*)_\ell :=S({E}^*)\cap \mathrm {Sym}^\ell (V^*)=\mathrm {Sym}^\ell (V^*)^N$
, and
$S({E}^*)_\ell :=S({E}^*)\cap \mathrm {Sym}^\ell (V^*)=\mathrm {Sym}^\ell (V^*)^N$
, and
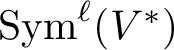 $\mathrm {Sym}^\ell (V^*)$
denotes the
$\mathrm {Sym}^\ell (V^*)$
denotes the
![]() $\ell $
th symmetric power of
$\ell $
th symmetric power of
![]() $V^*$
. On the other hand,
$V^*$
. On the other hand,
 $$ \begin{align*}\prod_{d\in\mathcal{D}_N}\Bigl(\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|\mathrm{Sym}^\ell({E}^*_{d})\bigr)(x^{d})^\ell\Bigr)=\prod_{d\in\mathcal{D}_N}\frac{1}{\mathrm{det}(1-x^{d}(g|_{{E}^*_{d}}))}=\prod_{i=1}^r\frac{1}{1-\epsilon_i^g({E})x_i^{d_i^N}}.\end{align*} $$
$$ \begin{align*}\prod_{d\in\mathcal{D}_N}\Bigl(\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|\mathrm{Sym}^\ell({E}^*_{d})\bigr)(x^{d})^\ell\Bigr)=\prod_{d\in\mathcal{D}_N}\frac{1}{\mathrm{det}(1-x^{d}(g|_{{E}^*_{d}}))}=\prod_{i=1}^r\frac{1}{1-\epsilon_i^g({E})x_i^{d_i^N}}.\end{align*} $$
Therefore,
 $$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell=\prod_{i=1}^r\frac{1}{1-\epsilon_i^g({E})x_i^{d_i^N}}.\end{align*} $$
$$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell=\prod_{i=1}^r\frac{1}{1-\epsilon_i^g({E})x_i^{d_i^N}}.\end{align*} $$
Because, for
![]() $n\in N$
,
$n\in N$
,
 $$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)x^\ell = \frac{1}{\mathrm{det}(1-x(ng|_{V^*}))},\end{align*} $$
$$ \begin{align*}\sum_{\ell\geq 0}\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)x^\ell = \frac{1}{\mathrm{det}(1-x(ng|_{V^*}))},\end{align*} $$
it remains to show that
 $$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}\Bigl(\sum_{\ell\geq 0}\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)x^\ell\Bigr)=\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell\end{align*} $$
$$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}\Bigl(\sum_{\ell\geq 0}\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)x^\ell\Bigr)=\sum_{\ell\geq 0}\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr)x^\ell\end{align*} $$
or, equivalently, that for each
![]() $\ell \geq 0$
we have that
$\ell \geq 0$
we have that
 $$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}\Bigl(\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)\Bigr)=\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr).\end{align*} $$
$$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}\Bigl(\mathrm{tr}\bigl(ng|\mathrm{Sym}^\ell(V^*)\bigr)\Bigr)=\mathrm{tr}\bigl(g|S({E}^*)_\ell\bigr).\end{align*} $$
To see this, note that the operator on
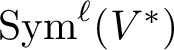 $\mathrm {Sym}^\ell (V^*)$
given by
$\mathrm {Sym}^\ell (V^*)$
given by
 $$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}ng=g\cdot\left(\frac{1}{|N|}\sum_{n\in N}n\right)=g\circ\mathrm{pr}^N_\ell,\end{align*} $$
$$ \begin{align*}\frac{1}{|N|}\sum_{n\in N}ng=g\cdot\left(\frac{1}{|N|}\sum_{n\in N}n\right)=g\circ\mathrm{pr}^N_\ell,\end{align*} $$
where
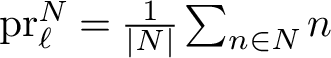 $\mathrm {pr}^N_\ell =\frac {1}{|N|}\sum _{n\in N} n$
is the projection from
$\mathrm {pr}^N_\ell =\frac {1}{|N|}\sum _{n\in N} n$
is the projection from
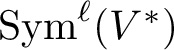 $\mathrm {Sym}^\ell (V^*)$
onto its g-stable subspace
$\mathrm {Sym}^\ell (V^*)$
onto its g-stable subspace
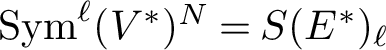 $\mathrm {Sym}^\ell (V^*)^N=S(E^*)_\ell $
, whence
$\mathrm {Sym}^\ell (V^*)^N=S(E^*)_\ell $
, whence
 $\mathrm {tr}\bigl ((g\circ \mathrm {pr}^N_\ell )|\mathrm {Sym}^\ell (V^*)\bigr )=\mathrm {tr}\bigl (g|S(E^*)_\ell \bigr )$
.
$\mathrm {tr}\bigl ((g\circ \mathrm {pr}^N_\ell )|\mathrm {Sym}^\ell (V^*)\bigr )=\mathrm {tr}\bigl (g|S(E^*)_\ell \bigr )$
.
Proposition 4.9 [Reference Bonnafé, Lehrer and Michel7, Theorem 3.1]
 $$ \begin{align*}\frac{1}{|N|}\sum_{n \in N} \frac{\det(1+u (ng)|_{{(V^\sigma)^*}})}{\det(1-x (ng)|_{{V^*}})} = \prod_{i=1}^r \frac{1+ \epsilon_{i}^{g}({U^N_\sigma}) u x^{e_i^N({V^\sigma})}}{1-\epsilon_{i}^{g}({E}) x^{d_i^N}}=\mathcal{P}^{Ng}_\sigma(x,x,u),\end{align*} $$
$$ \begin{align*}\frac{1}{|N|}\sum_{n \in N} \frac{\det(1+u (ng)|_{{(V^\sigma)^*}})}{\det(1-x (ng)|_{{V^*}})} = \prod_{i=1}^r \frac{1+ \epsilon_{i}^{g}({U^N_\sigma}) u x^{e_i^N({V^\sigma})}}{1-\epsilon_{i}^{g}({E}) x^{d_i^N}}=\mathcal{P}^{Ng}_\sigma(x,x,u),\end{align*} $$
Proof. The first equality is a special case of [Reference Bonnafé, Lehrer and Michel7, Theorem 3.1] (where we note that the change in sign from the
![]() $-u$
in their notation to
$-u$
in their notation to
![]() $+u$
in our notation is harmless), and the second equality follows directly from Proposition 4.8.
$+u$
in our notation is harmless), and the second equality follows directly from Proposition 4.8.
We obtain the following crucial specialisation of Proposition 4.8, which exploits the similarity between Proposition 4.9 and Proposition 4.8 and is inspired by [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3].
Proposition 4.10. For
![]() $g\in G$
, with notation as in Definition 4.7,
$g\in G$
, with notation as in Definition 4.7,
 $$ \begin{align}\lim_{x\to 1} \ |N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr) = t^{{\mathrm{fix}}_E (g)}\sum_{n \in N}\left(\prod\limits_{\bar{\lambda}_i(ng)\neq 1} \frac{1-\bar{\lambda}_i(ng)^\sigma}{1-\bar{\lambda}_i(ng)\vphantom{\Big|}} \right) q^{{\mathrm{fix}}_V (ng)}.\end{align} $$
$$ \begin{align}\lim_{x\to 1} \ |N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr) = t^{{\mathrm{fix}}_E (g)}\sum_{n \in N}\left(\prod\limits_{\bar{\lambda}_i(ng)\neq 1} \frac{1-\bar{\lambda}_i(ng)^\sigma}{1-\bar{\lambda}_i(ng)\vphantom{\Big|}} \right) q^{{\mathrm{fix}}_V (ng)}.\end{align} $$
Proof. Let us agree to index the pairs
![]() $(\epsilon _i^g({E}),d_i^N)$
and
$(\epsilon _i^g({E}),d_i^N)$
and
![]() $(\epsilon _i^g({U^N_\sigma }),e_i^N({V^\sigma }))$
in the multisets from Definition 4.7 such that
$(\epsilon _i^g({U^N_\sigma }),e_i^N({V^\sigma }))$
in the multisets from Definition 4.7 such that
![]() $\epsilon _i^g({E})=1$
for
$\epsilon _i^g({E})=1$
for
![]() $1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
(if
$1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
(if
![]() ${\mathrm {fix}}_{{E}}(g)\neq 0$
) and
${\mathrm {fix}}_{{E}}(g)\neq 0$
) and
![]() $\epsilon _i^g({U^N_\sigma })=1$
for
$\epsilon _i^g({U^N_\sigma })=1$
for
![]() $1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
(if
$1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
(if
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)\neq 0$
). By Proposition 4.8, the left-hand side of Equation (11) is
${\mathrm {fix}}_{{U^N_\sigma }}(g)\neq 0$
). By Proposition 4.8, the left-hand side of Equation (11) is
 $$ \begin{align*}|N|\cdot\lim_{x\to 1}\ \displaystyle\prod_{i=1}^r \left(\frac{\epsilon_i^g({U^N_\sigma}) qt(1-x) x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E}) x^{d_i^N}}+\frac{1-\epsilon_i^g({U^N_\sigma})x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E})x^{d_i^N}}\right).\end{align*} $$
$$ \begin{align*}|N|\cdot\lim_{x\to 1}\ \displaystyle\prod_{i=1}^r \left(\frac{\epsilon_i^g({U^N_\sigma}) qt(1-x) x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E}) x^{d_i^N}}+\frac{1-\epsilon_i^g({U^N_\sigma})x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E})x^{d_i^N}}\right).\end{align*} $$
By [Reference Bonnafé, Lehrer and Michel7, Proposition 3.2],
![]() ${\mathrm {fix}}_{{U^N_\sigma }} (g) \geq {\mathrm {fix}}_{{E}} (g)$
. We will compute the above limit for the partial products ranging over
${\mathrm {fix}}_{{U^N_\sigma }} (g) \geq {\mathrm {fix}}_{{E}} (g)$
. We will compute the above limit for the partial products ranging over
![]() $1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
,
$1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
,
![]() ${\mathrm {fix}}_{{E}}(g)+1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
and
${\mathrm {fix}}_{{E}}(g)+1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
and
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)+1\leq i \leq r$
separately.
${\mathrm {fix}}_{{U^N_\sigma }}(g)+1\leq i \leq r$
separately.
Because
![]() $\epsilon _i^g({E})=1=\epsilon _i^g({U^N_\sigma })$
for
$\epsilon _i^g({E})=1=\epsilon _i^g({U^N_\sigma })$
for
![]() $1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
, we have that
$1\leq i \leq {\mathrm {fix}}_{{E}}(g)$
, we have that
 $$ \begin{align*}\lim_{x\to 1}\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\frac{qt(1-x)x^{te_i^N({V^\sigma})}}{1-x^{d_i^N}}+\frac{1-x^{te_i^N({V^\sigma})}}{1-x^{d_i^N}}=\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\frac{qt+te_i^N({V^\sigma})}{d_i^N}.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\frac{qt(1-x)x^{te_i^N({V^\sigma})}}{1-x^{d_i^N}}+\frac{1-x^{te_i^N({V^\sigma})}}{1-x^{d_i^N}}=\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\frac{qt+te_i^N({V^\sigma})}{d_i^N}.\end{align*} $$
Because
![]() $\epsilon _i^g({E})\neq 1\neq \epsilon _i^g({U^N_\sigma })$
for
$\epsilon _i^g({E})\neq 1\neq \epsilon _i^g({U^N_\sigma })$
for
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)+1\leq i\leq r$
, we have that
${\mathrm {fix}}_{{U^N_\sigma }}(g)+1\leq i\leq r$
, we have that
 $$ \begin{align*}\lim_{x\to 1}\prod_{i={\mathrm{fix}}_{{U^N_\sigma}}(g)+1}^r\left(\frac{1+\epsilon_i^g({U^N_\sigma}) \bigl(qt(1-x) -1\bigr)x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E}) x^{d_i^N}}\right)=\prod_{i={\mathrm{fix}}_{{U^N_\sigma}}(g)+1}^r\frac{1-\epsilon_i^g({U^N_\sigma})}{1-\epsilon_i^g({E})}.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}\prod_{i={\mathrm{fix}}_{{U^N_\sigma}}(g)+1}^r\left(\frac{1+\epsilon_i^g({U^N_\sigma}) \bigl(qt(1-x) -1\bigr)x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E}) x^{d_i^N}}\right)=\prod_{i={\mathrm{fix}}_{{U^N_\sigma}}(g)+1}^r\frac{1-\epsilon_i^g({U^N_\sigma})}{1-\epsilon_i^g({E})}.\end{align*} $$
If the inequality
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)>{\mathrm {fix}}_{{E}}(g)$
is strict, so that
${\mathrm {fix}}_{{U^N_\sigma }}(g)>{\mathrm {fix}}_{{E}}(g)$
is strict, so that
![]() $\epsilon _i^g({E})\neq 1=\epsilon _i^g({U^N_\sigma })$
for
$\epsilon _i^g({E})\neq 1=\epsilon _i^g({U^N_\sigma })$
for
![]() ${\mathrm {fix}}_{{E}}(g)+1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
, then we see that for each such i the limit of the corresponding factor is
${\mathrm {fix}}_{{E}}(g)+1\leq i\leq {\mathrm {fix}}_{{U^N_\sigma }}(g)$
, then we see that for each such i the limit of the corresponding factor is
 $$ \begin{align*}\lim_{x\to 1}\frac{1+\bigl(qt(1-x)-1\bigr)x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E})x^{d_i^N}}=0.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}\frac{1+\bigl(qt(1-x)-1\bigr)x^{te_i^N({V^\sigma})}}{1-\epsilon_i^g({E})x^{d_i^N}}=0.\end{align*} $$
Therefore, if
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)>{\mathrm {fix}}_{{E}}(g)$
, then (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3])
${\mathrm {fix}}_{{U^N_\sigma }}(g)>{\mathrm {fix}}_{{E}}(g)$
, then (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3])
 $$ \begin{align*}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=0.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=0.\end{align*} $$
On the other hand, if
![]() ${\mathrm {fix}}_{{U^N_\sigma }}(g)={\mathrm {fix}}_{{E}}(g)$
, then (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3])
${\mathrm {fix}}_{{U^N_\sigma }}(g)={\mathrm {fix}}_{{E}}(g)$
, then (cf. [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3])
 $$ \begin{align*}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=t^{{\mathrm{fix}}_{{E}}(g)}\!\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\!(q+e_i^N({V^\sigma}))\!\!\prod_{i={\mathrm{fix}}_{{E}}(g)+1}^r\!\!\frac{1-\epsilon_i^g({U^N_\sigma})}{1-\epsilon_i^g({E})}d_i^N.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=t^{{\mathrm{fix}}_{{E}}(g)}\!\prod_{i=1}^{{\mathrm{fix}}_{{E}}(g)}\!(q+e_i^N({V^\sigma}))\!\!\prod_{i={\mathrm{fix}}_{{E}}(g)+1}^r\!\!\frac{1-\epsilon_i^g({U^N_\sigma})}{1-\epsilon_i^g({E})}d_i^N.\end{align*} $$
In any case, we have shown that the left-hand side of Equation (11) is
![]() $t^{{\mathrm {fix}}_{{E}}(g)}\cdot P(q)$
for some
$t^{{\mathrm {fix}}_{{E}}(g)}\cdot P(q)$
for some
![]() $P(q)\in \mathbb {C}[q]$
. To conclude the proof, it suffices to compare the left- and right-hand sides of Equation (11) at
$P(q)\in \mathbb {C}[q]$
. To conclude the proof, it suffices to compare the left- and right-hand sides of Equation (11) at
![]() $t=1$
. For this, we observe as in [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3] that, as a consequence of Proposition 4.9 and the arguments of [Reference Orlik and Solomon16, Theorem 3.3] that are now standard,
$t=1$
. For this, we observe as in [Reference Bonnafé, Lehrer and Michel7, Theorem 3.3] that, as a consequence of Proposition 4.9 and the arguments of [Reference Orlik and Solomon16, Theorem 3.3] that are now standard,
 $$ \begin{align*}\lim_{x\to 1} \ |N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x,q(1-x)-1\Bigr)=&\sum_{n\in N}\left(\prod_{i=1}^r\frac{1+\bar{\lambda}_i(ng)^\sigma u}{1-\bar{\lambda}_i(ng)x\vphantom{\Big|}}\right)\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ =&\sum_{n \in N}\left(\prod\limits_{\bar{\lambda}_i(ng)\neq 1} \frac{1-\bar{\lambda}_i(ng)^\sigma}{1-\bar{\lambda}_i(ng)\vphantom{\Big|}} \right) q^{{\mathrm{fix}}_V (ng)}.\\[-40pt]\end{align*} $$
$$ \begin{align*}\lim_{x\to 1} \ |N|\cdot\mathcal{P}^{Ng}_\sigma\Bigl(x,x,q(1-x)-1\Bigr)=&\sum_{n\in N}\left(\prod_{i=1}^r\frac{1+\bar{\lambda}_i(ng)^\sigma u}{1-\bar{\lambda}_i(ng)x\vphantom{\Big|}}\right)\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ =&\sum_{n \in N}\left(\prod\limits_{\bar{\lambda}_i(ng)\neq 1} \frac{1-\bar{\lambda}_i(ng)^\sigma}{1-\bar{\lambda}_i(ng)\vphantom{\Big|}} \right) q^{{\mathrm{fix}}_V (ng)}.\\[-40pt]\end{align*} $$
Corollary 4.11 Sum side specialisation
 $$ \begin{align*}\lim_{x\to 1}|G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)}.\end{align*} $$
$$ \begin{align*}\lim_{x\to 1}|G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\sum_{g \in G}\left( \prod_{\lambda_i(g) \neq 1} \frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right) q^{{\mathrm{fix}}_V (g)} t^{{\mathrm{fix}}_{E} (g)}.\end{align*} $$
Proof. Let
![]() $g_1,\dots ,g_{|H|}\in G$
be a full set of coset representatives for
$g_1,\dots ,g_{|H|}\in G$
be a full set of coset representatives for
![]() $G/N=H$
. Because
$G/N=H$
. Because
 $\mathcal {P}^G_\sigma (x,y,u)=\frac {1}{|H|}\sum _{j=1}^{|H|}\mathcal {P}^{Ng_j}_\sigma (x,y,u)$
and
$\mathcal {P}^G_\sigma (x,y,u)=\frac {1}{|H|}\sum _{j=1}^{|H|}\mathcal {P}^{Ng_j}_\sigma (x,y,u)$
and
![]() ${\mathrm {fix}}_{{E}}(g_j)={\mathrm {fix}}_{{E}}(ng_j)$
for any
${\mathrm {fix}}_{{E}}(g_j)={\mathrm {fix}}_{{E}}(ng_j)$
for any
![]() $n\in N$
, it follows from Proposition 4.10 that
$n\in N$
, it follows from Proposition 4.10 that
 $$ \begin{gather*}\lim_{x\to 1}\ |G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\sum_{j=1}^{|H|}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng_j}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\\ \begin{aligned} =&\sum_{j=1}^{|H|}t^{{\mathrm{fix}}_{{E}}(g_j)}\sum_{n\in N}\left(\prod_{\bar{\lambda}_i(ng_j)\neq 1}\frac{1-\bar{\lambda}_i(ng_j)^\sigma}{1-\bar{\lambda}_i(ng_j)\vphantom{\Big|}}\right)q^{{\mathrm{fix}}_V(ng_j)}\\ =&\sum_{g\in G}\left(\prod_{\bar{\lambda}_i(g)\neq 1}\frac{1-\bar{\lambda}_i(g)^\sigma}{1-\bar{\lambda}_i(g)\vphantom{\Big|}}\right)q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)},\end{aligned}\end{gather*} $$
$$ \begin{gather*}\lim_{x\to 1}\ |G|\cdot\mathcal{P}^G_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\sum_{j=1}^{|H|}\lim_{x\to 1}|N|\cdot\mathcal{P}^{Ng_j}_\sigma\Bigl(x,x^t,qt(1-x)-1\Bigr)=\\ \begin{aligned} =&\sum_{j=1}^{|H|}t^{{\mathrm{fix}}_{{E}}(g_j)}\sum_{n\in N}\left(\prod_{\bar{\lambda}_i(ng_j)\neq 1}\frac{1-\bar{\lambda}_i(ng_j)^\sigma}{1-\bar{\lambda}_i(ng_j)\vphantom{\Big|}}\right)q^{{\mathrm{fix}}_V(ng_j)}\\ =&\sum_{g\in G}\left(\prod_{\bar{\lambda}_i(g)\neq 1}\frac{1-\bar{\lambda}_i(g)^\sigma}{1-\bar{\lambda}_i(g)\vphantom{\Big|}}\right)q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)},\end{aligned}\end{gather*} $$
and our result follows after replacing g with
![]() $g^{-1}$
.
$g^{-1}$
.
Remark 4.12. As mentioned in the Introduction, the formula of Theorem 1.4 corresponding to the special case
![]() $\sigma =1$
becomes [Reference Arreche and Williams1, Theorem 1.5]
$\sigma =1$
becomes [Reference Arreche and Williams1, Theorem 1.5]
 $$ \begin{align}\sum_{g\in G} q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)}=\prod_{i=1}^r(qt+e_i^N(V)t+e_i^G({E})),\end{align} $$
$$ \begin{align}\sum_{g\in G} q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)}=\prod_{i=1}^r(qt+e_i^N(V)t+e_i^G({E})),\end{align} $$
which recovers Equation (2) for the reflection group G by evaluating at
![]() $t=1$
, because
$t=1$
, because
![]() ${E}\simeq {U^N}$
as G-modules in this case by Lemma 4.1 and
${E}\simeq {U^N}$
as G-modules in this case by Lemma 4.1 and
![]() $e_i^N(V)+e_i^G(E)=e_i^G(V)$
by Theorem 1.3, as discussed in Remark 4.2.
$e_i^N(V)+e_i^G(E)=e_i^G(V)$
by Theorem 1.3, as discussed in Remark 4.2.
On the other hand, specialising Equation (12) at
![]() $q=1$
and dividing by
$q=1$
and dividing by
![]() $|N|$
on both sides again recovers Equation (2) but this time for the reflection group H: the sum side follows from observing that
$|N|$
on both sides again recovers Equation (2) but this time for the reflection group H: the sum side follows from observing that
![]() ${\mathrm {fix}}_{{E}}(Ng)={\mathrm {fix}}_{{E}}(g)$
for every
${\mathrm {fix}}_{{E}}(Ng)={\mathrm {fix}}_{{E}}(g)$
for every
![]() $Ng\in H$
. The product side follows from the equality
$Ng\in H$
. The product side follows from the equality
![]() $d_i^N\cdot e_i^H({E})=e_i^G({E})$
proved in Theorem 1.3, which is compatible with the classical identities
$d_i^N\cdot e_i^H({E})=e_i^G({E})$
proved in Theorem 1.3, which is compatible with the classical identities
![]() $1+e_i^N(V)=d_i^N$
and
$1+e_i^N(V)=d_i^N$
and
![]() $\prod _{i=1}^rd_i^N=|N|$
by Remark 4.2.
$\prod _{i=1}^rd_i^N=|N|$
by Remark 4.2.
In fact, it is also possible to recover Equation (2) for the reflection group N from Equation (12). Because H acts faithfully on
![]() ${E}$
, we have
${E}$
, we have
![]() $N=\{g\in G \ | \ {\mathrm {fix}}_{{E}}(g)=r\}$
, and therefore applying
$N=\{g\in G \ | \ {\mathrm {fix}}_{{E}}(g)=r\}$
, and therefore applying
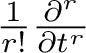 $\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
to the sum-side of Equation (12) recovers the sum side of Equation (2) for N. That the analogous result obtains for the product side follows from the well-known higher Leibniz rule for the Hasse-Schmidt derivations
$\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
to the sum-side of Equation (12) recovers the sum side of Equation (2) for N. That the analogous result obtains for the product side follows from the well-known higher Leibniz rule for the Hasse-Schmidt derivations
 $\delta ^{(i)}:=\frac {1}{i!}\frac {\partial ^i}{\partial t^i}$
, which yield
$\delta ^{(i)}:=\frac {1}{i!}\frac {\partial ^i}{\partial t^i}$
, which yield
 $$ \begin{align*}\delta^{(r)}\left(\prod_{i=1}^r(qt+e_i^N(V)t+e_i^G({E}))\right)=\prod_{i=1}^r\delta^{(1)}(qt+e_i^N(V)t+e_i^G({E}))=\prod_{i=1}^r(q+e_i^N(V)).\end{align*} $$
$$ \begin{align*}\delta^{(r)}\left(\prod_{i=1}^r(qt+e_i^N(V)t+e_i^G({E}))\right)=\prod_{i=1}^r\delta^{(1)}(qt+e_i^N(V)t+e_i^G({E}))=\prod_{i=1}^r(q+e_i^N(V)).\end{align*} $$
Similarly, as we mentioned in the Introduction, for arbitrary
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
the formula of Theorem 1.4
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _G)/\mathbb {Q})$
the formula of Theorem 1.4
 $$ \begin{align} \sum_{g\in G}\left(\prod_{\lambda_i(g)\neq 1}\frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right)q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)}=\prod_{i=1}^r(qt+e_i^N({V^\sigma})t+e_i^G({U^N_\sigma})) \end{align} $$
$$ \begin{align} \sum_{g\in G}\left(\prod_{\lambda_i(g)\neq 1}\frac{1-\lambda_i(g)^\sigma}{1-\lambda_i(g)}\right)q^{{\mathrm{fix}}_V(g)}t^{{\mathrm{fix}}_{{E}}(g)}=\prod_{i=1}^r(qt+e_i^N({V^\sigma})t+e_i^G({U^N_\sigma})) \end{align} $$
recovers Theorem 1.1 by evaluating at
![]() $t=1$
, because
$t=1$
, because
![]() $e_i^N({V^\sigma })+e_i^G({U^N_\sigma })=e_i^G({V^\sigma })$
by Theorem 1.3. The above arguments also show that we recover Theorem 1.1 for the reflection group N again by applying
$e_i^N({V^\sigma })+e_i^G({U^N_\sigma })=e_i^G({V^\sigma })$
by Theorem 1.3. The above arguments also show that we recover Theorem 1.1 for the reflection group N again by applying
 $\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
to both sides of Equation (13).
$\frac {1}{r!}\frac {\partial ^r}{\partial t^r}$
to both sides of Equation (13).
It would be desirable to recover Theorem 1.1 for the reflection group H from Theorem 1.4 in analogy with the case
![]() $\sigma =1$
, by evaluating Equation (13) at
$\sigma =1$
, by evaluating Equation (13) at
![]() $q=1$
and dividing by
$q=1$
and dividing by
![]() $|N|$
on both sides. But in this case we obtain something else: letting
$|N|$
on both sides. But in this case we obtain something else: letting
![]() $g_1,\dots ,g_{|H|}\in G$
be a full set of coset representatives for
$g_1,\dots ,g_{|H|}\in G$
be a full set of coset representatives for
![]() $H=G/N$
, evaluating Equation (13) at
$H=G/N$
, evaluating Equation (13) at
![]() $q=1$
yields
$q=1$
yields
 $$ \begin{align*}\sum_{j=1}^{|H|}\left(\sum_{n\in N}\left(\prod_{\lambda_i(ng_j)\neq 1}\frac{1-\lambda_i(ng_j)^\sigma}{1-\lambda_i(ng_j)}\right)\right)t^{{\mathrm{fix}}_{{E}}(g_j)}=\prod_{i=1}^r((e_i^N({V^\sigma})+1)t+e_i^G({U^N_\sigma})),\end{align*} $$
$$ \begin{align*}\sum_{j=1}^{|H|}\left(\sum_{n\in N}\left(\prod_{\lambda_i(ng_j)\neq 1}\frac{1-\lambda_i(ng_j)^\sigma}{1-\lambda_i(ng_j)}\right)\right)t^{{\mathrm{fix}}_{{E}}(g_j)}=\prod_{i=1}^r((e_i^N({V^\sigma})+1)t+e_i^G({U^N_\sigma})),\end{align*} $$
which does not immediately compare to the statement of Theorem 1.1 for the reflection group H:
 $$ \begin{align*} \sum_{j=1}^{|H|}\left(\prod_{\bar{\epsilon}_i^{\, g_j}({E})\neq 1}\frac{1-\bar{\epsilon}_i^{\, g_j}({E})^\sigma}{1-\bar{\epsilon}_i^{\, g_j}({E})\vphantom{\Big|}}\right)t^{{\mathrm{fix}}_{{E}}(g_j)}=\prod_{i=1}^r(t+e_i^H({E^\sigma})),\end{align*} $$
$$ \begin{align*} \sum_{j=1}^{|H|}\left(\prod_{\bar{\epsilon}_i^{\, g_j}({E})\neq 1}\frac{1-\bar{\epsilon}_i^{\, g_j}({E})^\sigma}{1-\bar{\epsilon}_i^{\, g_j}({E})\vphantom{\Big|}}\right)t^{{\mathrm{fix}}_{{E}}(g_j)}=\prod_{i=1}^r(t+e_i^H({E^\sigma})),\end{align*} $$
where compatibly with Definition 4.7 the
![]() $\bar {\epsilon }_i^{\, g_j}({E})$
denote the eigenvalues of
$\bar {\epsilon }_i^{\, g_j}({E})$
denote the eigenvalues of
![]() $g_j\in G$
acting on
$g_j\in G$
acting on
![]() ${E}$
.
${E}$
.
5 Reflexponents revisited
Fix G a complex reflection group of rank r with reflection representation V. Call an r-dimensional representation M of G factorising if M has dimension r and
 $$ \begin{align*}\sum_{g \in G} q^{\mathrm{fix}_V(g)} t^{\mathrm{fix}_M(g)} = \prod_{i=1}^r \Big(qt+(e_i^G(V)-m_i)t+ m_i\Big),\end{align*} $$
$$ \begin{align*}\sum_{g \in G} q^{\mathrm{fix}_V(g)} t^{\mathrm{fix}_M(g)} = \prod_{i=1}^r \Big(qt+(e_i^G(V)-m_i)t+ m_i\Big),\end{align*} $$
for some nonnegative integers
![]() $m_1,\ldots ,m_r$
. More generally, call a representation M of G of dimension
$m_1,\ldots ,m_r$
. More generally, call a representation M of G of dimension
![]() $\dim M \leq r$
factorising if it is factorising in the above sense after adding in
$\dim M \leq r$
factorising if it is factorising in the above sense after adding in
![]() $r-\dim M$
copies of the trivial representation.
$r-\dim M$
copies of the trivial representation.
A case-by-case construction of a factorising representation
![]() $M_{\mathcal {H}}$
associated to an arbitrary orbit of reflecting hyperplanes
$M_{\mathcal {H}}$
associated to an arbitrary orbit of reflecting hyperplanes
![]() $\mathcal {H}$
was presented in [Reference Williams22], with two unexplained exceptions. These factorising representations further restricted to the reflection representation of a parabolic subgroup supported on
$\mathcal {H}$
was presented in [Reference Williams22], with two unexplained exceptions. These factorising representations further restricted to the reflection representation of a parabolic subgroup supported on
![]() $\mathcal {H}$
. We can now give a uniform explanation for those ad hoc identities, including the two exceptions left unexplained in [Reference Williams22, Section 5.1].
$\mathcal {H}$
. We can now give a uniform explanation for those ad hoc identities, including the two exceptions left unexplained in [Reference Williams22, Section 5.1].
Let
![]() $\mathcal {H}$
be an orbit of hyperplanes, write
$\mathcal {H}$
be an orbit of hyperplanes, write
![]() $\mathcal {R}_{\mathcal {H}}$
for the set of reflections fixing some
$\mathcal {R}_{\mathcal {H}}$
for the set of reflections fixing some
![]() $H \in \mathcal {H}$
and let
$H \in \mathcal {H}$
and let
![]() $N_{\mathcal {H}} = \left \langle \mathcal {R}_{\mathcal {H}} \right \rangle $
be the subgroup generated by reflections around hyperplanes in
$N_{\mathcal {H}} = \left \langle \mathcal {R}_{\mathcal {H}} \right \rangle $
be the subgroup generated by reflections around hyperplanes in
![]() $\mathcal {H}$
. Because these reflections form a conjugacy class in G,
$\mathcal {H}$
. Because these reflections form a conjugacy class in G,
![]() $N_{\mathcal {H}}$
is a normal reflection subgroup of G. Furthermore,
$N_{\mathcal {H}}$
is a normal reflection subgroup of G. Furthermore,
-
(i) the quotient
 $G/N_{\mathcal {H}}$
acts by reflections on the vector space of
$G/N_{\mathcal {H}}$
acts by reflections on the vector space of
 $N_{\mathcal {H}}$
-orbits
$N_{\mathcal {H}}$
-orbits
 $M_{\mathcal {H}}$
,
$M_{\mathcal {H}}$
, -
(ii) this G-representation
 $M_{\mathcal {H}}$
is factorising by Theorem 1.4 and
$M_{\mathcal {H}}$
is factorising by Theorem 1.4 and -
(iii) the mysterious indexing of the reflexponents (i.e., the
 $e_i^G(M_{\mathcal {H}})$
) left unexplained in [Reference Williams22] is now explained in Remark 3.1.
$e_i^G(M_{\mathcal {H}})$
) left unexplained in [Reference Williams22] is now explained in Remark 3.1.
Corollary 5.1. For
![]() $\mathcal {H}$
an orbit of hyperplanes and
$\mathcal {H}$
an orbit of hyperplanes and
![]() $N_{\mathcal {H}} = \left \langle \mathcal {R}_{\mathcal {H}} \right \rangle ,$
the representation
$N_{\mathcal {H}} = \left \langle \mathcal {R}_{\mathcal {H}} \right \rangle ,$
the representation
![]() $M_{\mathcal {H}}$
is factorising.
$M_{\mathcal {H}}$
is factorising.
We can also explain the two exceptional factorising representations from [Reference Williams22]:
-
• Following the conventions of [Reference Marin and Michel15],
 $G=G_{13}=\langle s,t,u\rangle $
was observed in [Reference Williams22, Section 5.1] to have a 2-dimensional representation with the factorising property. The group
$G=G_{13}=\langle s,t,u\rangle $
was observed in [Reference Williams22, Section 5.1] to have a 2-dimensional representation with the factorising property. The group
 $N = \langle gsg^{-1}: g \in G \rangle $
(fixing the conjugacy class
$N = \langle gsg^{-1}: g \in G \rangle $
(fixing the conjugacy class
 $\mathcal {H}_s$
) is a normal subgroup isomorphic to
$\mathcal {H}_s$
) is a normal subgroup isomorphic to
 $G(4,2,2)$
and the quotient
$G(4,2,2)$
and the quotient
 $G/N \simeq W(A_2)\simeq \mathfrak {S}_3$
gives the unexplained 2-dimensional factorising representation in this case.
$G/N \simeq W(A_2)\simeq \mathfrak {S}_3$
gives the unexplained 2-dimensional factorising representation in this case. -
• For
 $G=G(ab,b,r)=\langle s,t_2,t_2',t_3,\ldots ,t_r\rangle $
with
$G=G(ab,b,r)=\langle s,t_2,t_2',t_3,\ldots ,t_r\rangle $
with
 $a,b>1$
and
$a,b>1$
and
 $r>2$
, we can take
$r>2$
, we can take
 $N= \langle gsg^{-1}: g \in G \rangle $
. N is a normal subgroup of G isomorphic to
$N= \langle gsg^{-1}: g \in G \rangle $
. N is a normal subgroup of G isomorphic to
 $(C_a)^r$
(it consists of diagonal matrices whose diagonal entries are ath roots of unity). The quotient
$(C_a)^r$
(it consists of diagonal matrices whose diagonal entries are ath roots of unity). The quotient
 $G/N \simeq G(b,b,r)$
gives the unexplained r-dimensional factorising representation in [Reference Williams22, Section 5.2].
$G/N \simeq G(b,b,r)$
gives the unexplained r-dimensional factorising representation in [Reference Williams22, Section 5.2].
6 Classification of Normal Reflection Subgroups
In this section, we state the classification of normal reflection subgroups of irreducible complex reflection groups.
Recall that
![]() $G(ab,b,r)$
is given in its standard reflection representation as the set of
$G(ab,b,r)$
is given in its standard reflection representation as the set of
![]() $r \times r$
monomial matrices whose every nonzero entry is an
$r \times r$
monomial matrices whose every nonzero entry is an
![]() $(ab)$
th root of unity and in which the product of the nonzero entries is an ath root of unity. The following theorem identifies the normal reflection subgroups of the infinite family
$(ab)$
th root of unity and in which the product of the nonzero entries is an ath root of unity. The following theorem identifies the normal reflection subgroups of the infinite family
![]() $G(ab,b,r)$
.
$G(ab,b,r)$
.
Theorem 6.1 [Reference Lehrer and Taylor14, Chapter 2]
Fix positive integers a and b, and let
![]() $a=de$
.
$a=de$
.
For rank
![]() $r=1$
,
$r=1$
,
![]() $G(ab,b,1)=C_a$
has normal subgroups and quotients
$G(ab,b,1)=C_a$
has normal subgroups and quotients
-
(1.a)
 $C_a / C_d \simeq C_e$
.
$C_a / C_d \simeq C_e$
.
For rank
![]() $r=2$
, the normal subgroups and quotients are
$r=2$
, the normal subgroups and quotients are
-
(2.a)
 $G(ab,b,2)/(C_d)^2 \simeq G(eb,b,2)$
,
$G(ab,b,2)/(C_d)^2 \simeq G(eb,b,2)$
, -
(2.b)
 $G(ab,b,2)/G(ab,db,2) \simeq C_d$
,
$G(ab,b,2)/G(ab,db,2) \simeq C_d$
, -
(2.c)
 $G(2ab,2d,2)/G(ab,a,2) \simeq C_2 \times C_e$
.
$G(2ab,2d,2)/G(ab,a,2) \simeq C_2 \times C_e$
.
For rank
![]() $r\geq 3$
, the normal subgroups and quotients are
$r\geq 3$
, the normal subgroups and quotients are
-
(r.a)
 $G(ab,b,r)/(C_d)^r \simeq G(eb,b,r)$
and
$G(ab,b,r)/(C_d)^r \simeq G(eb,b,r)$
and -
(r.b)
 $G(ab,b,r)/G(ab,db,r) \simeq C_d$
.
$G(ab,b,r)/G(ab,db,r) \simeq C_d$
.
In cases (r.a) for
![]() $r\geq 1$
, the polycyclic group
$r\geq 1$
, the polycyclic group
![]() $N=(C_d)^r$
is included in G as diagonal matrices with each nonzero entry a dth root of unity. In cases (r.b) for
$N=(C_d)^r$
is included in G as diagonal matrices with each nonzero entry a dth root of unity. In cases (r.b) for
![]() $r\geq 2$
, the normal reflection subgroup
$r\geq 2$
, the normal reflection subgroup
![]() $N=G(ab,db,r)$
is included in G via its standard reflection representation on
$N=G(ab,db,r)$
is included in G via its standard reflection representation on
![]() $\mathbb {C}^r$
. In case (
$\mathbb {C}^r$
. In case (
![]() $2$
.c), the normal reflection subgroup
$2$
.c), the normal reflection subgroup
![]() $N=G(ab,a,2)$
occurs twice in
$N=G(ab,a,2)$
occurs twice in
![]() $G=G(2ab,2d,2)$
: once via its standard reflection representation, and once as the group generated by the reflections
$G=G(2ab,2d,2)$
: once via its standard reflection representation, and once as the group generated by the reflections
![]() $\{\mathrm{diag}(\zeta_b^k,1),\ \mathrm{diag}(1,\zeta_b^k) \ | \ k=1,\dots,b-1\}$
(when
$\{\mathrm{diag}(\zeta_b^k,1),\ \mathrm{diag}(1,\zeta_b^k) \ | \ k=1,\dots,b-1\}$
(when
![]() $b\neq 1$
) along with the reflections
$b\neq 1$
) along with the reflections
 $$ \begin{align*}\left\{\begin{pmatrix}0 & \zeta_{2ab}^{2k-1} \\ \zeta_{2ab}^{-2k+1} & 0\end{pmatrix} \ \middle| \ k=0,\dots,ab-1 \right\}.\end{align*} $$
$$ \begin{align*}\left\{\begin{pmatrix}0 & \zeta_{2ab}^{2k-1} \\ \zeta_{2ab}^{-2k+1} & 0\end{pmatrix} \ \middle| \ k=0,\dots,ab-1 \right\}.\end{align*} $$
Independent of the factorization
![]() $a=de$
, these two copies of N are conjugate in
$a=de$
, these two copies of N are conjugate in
![]() $\mathrm {GL}_2(\mathbb {C})$
by the matrix
$\mathrm {GL}_2(\mathbb {C})$
by the matrix
![]() $\mathrm{diag}(1,\zeta_{2ab})$
, which normalizes G. There are other coincidences in rank
$\mathrm{diag}(1,\zeta_{2ab})$
, which normalizes G. There are other coincidences in rank
![]() $r=2$
where G contains several copies of ‘the same’ normal reflection subgroup N, related to the well-known isomorphisms
$r=2$
where G contains several copies of ‘the same’ normal reflection subgroup N, related to the well-known isomorphisms
![]() $G(4,4,2)\simeq G(2,1,2)$
and
$G(4,4,2)\simeq G(2,1,2)$
and
![]() $G(2,2,2)\simeq C_2\times C_2$
(see [Reference Lehrer and Taylor14, Example 2.11]). For example,
$G(2,2,2)\simeq C_2\times C_2$
(see [Reference Lehrer and Taylor14, Example 2.11]). For example,
![]() $G(4,2,2)$
contains the dihedral group of order 8 as a normal reflection subgroup in three different ways:
$G(4,2,2)$
contains the dihedral group of order 8 as a normal reflection subgroup in three different ways:
![]() $G(4,4,2)$
in one way as case (
$G(4,4,2)$
in one way as case (
![]() $2$
.b) and
$2$
.b) and
![]() $G(2,1,2)$
in two ways as case (
$G(2,1,2)$
in two ways as case (
![]() $2$
.c). Similarly,
$2$
.c). Similarly,
![]() $G(4,2,2)$
contains
$G(4,2,2)$
contains
![]() $C_2 \times C_2$
in three ways:
$C_2 \times C_2$
in three ways:
![]() $(C_2)^2$
in one way as case (
$(C_2)^2$
in one way as case (
![]() $2$
.a) and
$2$
.a) and
![]() $G(2,2,2)$
in two ways as case (
$G(2,2,2)$
in two ways as case (
![]() $2$
.c).
$2$
.c).
The exceptional (that is, primitive) irreducible complex reflection groups G and their normal reflection subgroups N are listed in Table 1. This classification was computed with Sage [21] using the code available at [Reference Arreche and Williams2]. Most examples occur in rank
![]() $r=2$
. In rank
$r=2$
. In rank
![]() $r\geq 3$
, every reflection has order
$r\geq 3$
, every reflection has order
![]() $2$
or
$2$
or
![]() $3$
[Reference Lehrer and Taylor14, Theorem 8.4] and the only exceptional groups with more than a single orbit of reflections are
$3$
[Reference Lehrer and Taylor14, Theorem 8.4] and the only exceptional groups with more than a single orbit of reflections are
![]() $G_{26}$
and
$G_{26}$
and
![]() $G_{28}$
[Reference Lehrer and Taylor14, Table D.2], which leads to the four nontrivial exceptional examples listed in Table 1 in rank
$G_{28}$
[Reference Lehrer and Taylor14, Table D.2], which leads to the four nontrivial exceptional examples listed in Table 1 in rank
![]() $r\geq 3$
.
$r\geq 3$
.
Table 1 The exceptional groups, their nontrivial normal reflection subgroups and the corresponding quotient reflection groups.

An isomorphism type of N is unique up to conjugation in
![]() $\mathrm {GL}_r(\mathbb {C})$
sending isomorphic normal reflection subgroups to each other while stabilising the reflection representation of G. In fact, there are only two instances in the exceptional groups (
$\mathrm {GL}_r(\mathbb {C})$
sending isomorphic normal reflection subgroups to each other while stabilising the reflection representation of G. In fact, there are only two instances in the exceptional groups (
![]() $G_5 \triangleright G_4$
and
$G_5 \triangleright G_4$
and
![]() $G_{28} \triangleright G(2,2,4)$
) where an isomorphism type appears as a normal subgroup more than once. We gather the situations where the same isomorphism type of N occurs more than once as a normal reflection subgroup of G in the following result, where
$G_{28} \triangleright G(2,2,4)$
) where an isomorphism type appears as a normal subgroup more than once. We gather the situations where the same isomorphism type of N occurs more than once as a normal reflection subgroup of G in the following result, where
![]() $N_{(i)}$
denote the different isomorphic copies of the same normal reflection subgroup
$N_{(i)}$
denote the different isomorphic copies of the same normal reflection subgroup
![]() $N\triangleleft G$
.
$N\triangleleft G$
.
Theorem 6.2. Suppose that G is an irreducible complex reflection group admitting normal reflection subgroups
![]() $N_{(1)},\dots ,N_{(k)}$
for
$N_{(1)},\dots ,N_{(k)}$
for
![]() $k\geq 2$
that are pairwise isomorphic (as abstract groups) but not equal in G. Then
$k\geq 2$
that are pairwise isomorphic (as abstract groups) but not equal in G. Then
![]() $k\in \{2,3\}$
and the normaliser of G in
$k\in \{2,3\}$
and the normaliser of G in
![]() $\mathrm {GL}(V)$
permutes
$\mathrm {GL}(V)$
permutes
![]() $\{N_{(1)},\dots ,N_{(k)}\}$
transitively under conjugation. Moreover, precisely one of the following possibilities occurs:
$\{N_{(1)},\dots ,N_{(k)}\}$
transitively under conjugation. Moreover, precisely one of the following possibilities occurs:
-
(1)
 $G=G(4,2,2)$
and there are
$G=G(4,2,2)$
and there are
 $k=3$
different normal reflection subgroups isomorphic to the dihedral group of order
$k=3$
different normal reflection subgroups isomorphic to the dihedral group of order
 $8$
:
$8$
: -
(2)
 $G=G(4,2,2)$
and there are
$G=G(4,2,2)$
and there are
 $k=3$
different normal reflection subgroups isomorphic to the Klein
$k=3$
different normal reflection subgroups isomorphic to the Klein
 $4$
-group:
$4$
-group: -
(3)
 $G=G(2ab,2d,2) \neq G(4,2,2)$
with d a factor of a and there are
$G=G(2ab,2d,2) \neq G(4,2,2)$
with d a factor of a and there are
 $k=2$
different normal reflection subgroups isomorphic to
$k=2$
different normal reflection subgroups isomorphic to
 $G(ab,a,2)$
:
$G(ab,a,2)$
:-
(a)
 $N_{(1)}=G(ab,a,2)$
as in Theorem 6.1(
$N_{(1)}=G(ab,a,2)$
as in Theorem 6.1(
 $2$
.c);
$2$
.c); -
(b)
 $N_{(2)}=\mathrm {diag}(1,\zeta _{2ab}^{-1})\cdot N_{(1)}\cdot \mathrm {diag}(1,\zeta _{2ab})$
.
$N_{(2)}=\mathrm {diag}(1,\zeta _{2ab}^{-1})\cdot N_{(1)}\cdot \mathrm {diag}(1,\zeta _{2ab})$
.
-
-
(4)
 $G=G_5$
and there are
$G=G_5$
and there are
 $k=2$
different normal reflection subgroups isomorphic to
$k=2$
different normal reflection subgroups isomorphic to
 $G_4$
.
$G_4$
. -
(5)
 $G=G_{28}$
and there are
$G=G_{28}$
and there are
 $k=2$
different normal reflection subgroups isomorphic to
$k=2$
different normal reflection subgroups isomorphic to
 $G(2,2,4)$
.
$G(2,2,4)$
.
Proof. By Theorem 6.1 and Table 1, the possibilities above are exhaustive, and it is clear that they are mutually exclusive.
It remains to show that any two isomorphic normal reflection subgroups of G are conjugate under an element of the normaliser of G. In every situation listed above, except for
![]() $G=G_{28}$
, we can find a complex reflection group W that contains G as a normal reflection subgroup (in its standard reflection representation) but that does not contain (the isomorphism type of) N as a normal reflection subgroup. Because there are at most three isomorphic copies of N in each case, they must then form a single conjugacy class in W.
$G=G_{28}$
, we can find a complex reflection group W that contains G as a normal reflection subgroup (in its standard reflection representation) but that does not contain (the isomorphism type of) N as a normal reflection subgroup. Because there are at most three isomorphic copies of N in each case, they must then form a single conjugacy class in W.
In cases (1) and (2), we can take W to be any of
![]() $G_6$
,
$G_6$
,
![]() $G_7$
,
$G_7$
,
![]() $G_8$
,
$G_8$
,
![]() $G_9$
,
$G_9$
,
![]() $G_{10}$
,
$G_{10}$
,
![]() $G_{11}$
,
$G_{11}$
,
![]() $G_{13}$
or
$G_{13}$
or
![]() $G_{15}$
because all of these contain
$G_{15}$
because all of these contain
![]() $G=G(4,2,2)$
as their only imprimitive normal reflection subgroup according to Table 1.
$G=G(4,2,2)$
as their only imprimitive normal reflection subgroup according to Table 1.
In case (3), we can take
![]() $W=G(2ab,1,2)$
, which contains
$W=G(2ab,1,2)$
, which contains
![]() $G=G(2ab,2d,2)$
as a normal reflection subgroup as in Theorem 6.1(2.b) for each factor d of a, but does not normalise
$G=G(2ab,2d,2)$
as a normal reflection subgroup as in Theorem 6.1(2.b) for each factor d of a, but does not normalise
![]() $N=G(ab,a,2)$
.
$N=G(ab,a,2)$
.
In case (4), we can take W to be any of
![]() $G_7$
,
$G_7$
,
![]() $G_{10}$
,
$G_{10}$
,
![]() $G_{11}$
,
$G_{11}$
,
![]() $G_{14}$
or
$G_{14}$
or
![]() $G_{15}$
because all of these contain
$G_{15}$
because all of these contain
![]() $G_5$
as a normal reflection subgroup but do not normalise
$G_5$
as a normal reflection subgroup but do not normalise
![]() $G_4$
.
$G_4$
.
Finally, in case (5) it is not possible to find a complex reflection group W containing
![]() $G=G_{28}$
as a normal reflection subgroup because
$G=G_{28}$
as a normal reflection subgroup because
![]() $G_{28}$
is the only irreducible complex reflection group admitting a nontrivial normal reflection subgroup in rank
$G_{28}$
is the only irreducible complex reflection group admitting a nontrivial normal reflection subgroup in rank
![]() $r\geq 4$
. To see that the two isomorphic copies of
$r\geq 4$
. To see that the two isomorphic copies of
![]() $N\simeq G(2,2,4)$
in
$N\simeq G(2,2,4)$
in
![]() $G=G_{28}$
are conjugate under an element of the normaliser of G in
$G=G_{28}$
are conjugate under an element of the normaliser of G in
![]() $\mathrm {GL}_4(\mathbb {C})$
, consider the set of reflecting hyperplanes for
$\mathrm {GL}_4(\mathbb {C})$
, consider the set of reflecting hyperplanes for
![]() $G_{28}$
, which are the orthogonal complements (with respect to the standard Hermitian inner product in
$G_{28}$
, which are the orthogonal complements (with respect to the standard Hermitian inner product in
![]() $\mathbb {C}^4$
) of the lines in
$\mathbb {C}^4$
) of the lines in
![]() $\mathcal {L}_1\cup \mathcal {L}_2\cup \mathcal {L}_3$
defined by (cf. [Reference Lehrer and Taylor14, Section 7.6.2]):
$\mathcal {L}_1\cup \mathcal {L}_2\cup \mathcal {L}_3$
defined by (cf. [Reference Lehrer and Taylor14, Section 7.6.2]):
 $$ \begin{gather*}\mathcal{L}_1=\left\{\mathbb{C}\cdot e_i \ \middle| \ 1\leq i\leq 4\right\};\qquad \mathcal{L}_2=\left\{\mathbb{C}\cdot\tfrac{1}{2}(e_1 \pm e_2 \pm e_3\pm e_4)\right\}; \quad\text{and} \\ \mathcal{L}_3=\left\{\mathbb{C}\cdot (e_i\pm e_j) \ \middle| \ 1\leq i<j\leq 4\right\},\end{gather*} $$
$$ \begin{gather*}\mathcal{L}_1=\left\{\mathbb{C}\cdot e_i \ \middle| \ 1\leq i\leq 4\right\};\qquad \mathcal{L}_2=\left\{\mathbb{C}\cdot\tfrac{1}{2}(e_1 \pm e_2 \pm e_3\pm e_4)\right\}; \quad\text{and} \\ \mathcal{L}_3=\left\{\mathbb{C}\cdot (e_i\pm e_j) \ \middle| \ 1\leq i<j\leq 4\right\},\end{gather*} $$
where
![]() $e_i$
denotes the standard basis vector with
$e_i$
denotes the standard basis vector with
![]() $1$
in the ith entry and
$1$
in the ith entry and
![]() $0$
elsewhere. There are two orbits of reflecting hyperplanes for
$0$
elsewhere. There are two orbits of reflecting hyperplanes for
![]() $G_{28}=W(F_4)$
(the Weyl group of type
$G_{28}=W(F_4)$
(the Weyl group of type
![]() $F_4$
and a real reflection group), corresponding to
$F_4$
and a real reflection group), corresponding to
![]() $\mathcal {L}_1\cup \mathcal {L}_2$
(the lines spanned by the short roots) and
$\mathcal {L}_1\cup \mathcal {L}_2$
(the lines spanned by the short roots) and
![]() $\mathcal {L}_3$
(the lines spanned by the long roots). The reflections around the
$\mathcal {L}_3$
(the lines spanned by the long roots). The reflections around the
![]() $12$
hyperplanes corresponding to
$12$
hyperplanes corresponding to
![]() $\mathcal {L}_3$
generate the normal reflection subgroup
$\mathcal {L}_3$
generate the normal reflection subgroup
![]() $N_{(1)}=G(2,2,4)$
acting in its standard reflection representation. The other normal reflection subgroup
$N_{(1)}=G(2,2,4)$
acting in its standard reflection representation. The other normal reflection subgroup
![]() $N_{(2)}$
is generated by the reflections around the other
$N_{(2)}$
is generated by the reflections around the other
![]() $12$
hyperplanes corresponding to
$12$
hyperplanes corresponding to
![]() $\mathcal {L}_1\cup \mathcal {L}_2$
. To conclude the proof, note that the real orthogonal matrix
$\mathcal {L}_1\cup \mathcal {L}_2$
. To conclude the proof, note that the real orthogonal matrix
 $$ \begin{align*}P:=\frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ -1 & 0 & 1 & 0\end{pmatrix} \end{align*} $$
$$ \begin{align*}P:=\frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ -1 & 0 & 1 & 0\end{pmatrix} \end{align*} $$
exchanges the two
![]() $G_{28}$
-orbits of reflecting hyperplanes
$G_{28}$
-orbits of reflecting hyperplanes
![]() $\mathcal {L}_1\cup \mathcal {L}_2 \leftrightarrow \mathcal {L}_3$
(identifying
$\mathcal {L}_1\cup \mathcal {L}_2 \leftrightarrow \mathcal {L}_3$
(identifying
![]() $\mathcal {L}_1$
with the set of lines
$\mathcal {L}_1$
with the set of lines
![]() $\mathbb {C}\cdot (e_i\pm e_j)\in \mathcal {L}_3$
such that
$\mathbb {C}\cdot (e_i\pm e_j)\in \mathcal {L}_3$
such that
![]() $j-i=2$
). Hence, P normalises
$j-i=2$
). Hence, P normalises
![]() $G_{28}$
and exchanges
$G_{28}$
and exchanges
![]() $N_{(1)}$
and
$N_{(1)}$
and
![]() $N_{(2)}$
under conjugation.
$N_{(2)}$
under conjugation.
7 Examples
In this section we illustrate our results with examples, beginning with the cyclic groups in Section 7.1, continuing with the infinite family in Section 7.2 and concluding with a non-well-generated exceptional example in Section 7.3.
7.1 Cyclic Groups
Consider
![]() $G=C_a=\langle c\rangle $
, the cyclic group of order a, acting on
$G=C_a=\langle c\rangle $
, the cyclic group of order a, acting on
![]() $V=\mathbb {C}$
via
$V=\mathbb {C}$
via
![]() $c\mapsto \zeta _a^{-1}$
, where
$c\mapsto \zeta _a^{-1}$
, where
![]() $\zeta _a$
is a primitive ath root of unity. Verifying Theorem 1.1 and determining the Orlik-Solomon space
$\zeta _a$
is a primitive ath root of unity. Verifying Theorem 1.1 and determining the Orlik-Solomon space
![]() ${U^G_\sigma }$
from Definition 2.9 for
${U^G_\sigma }$
from Definition 2.9 for
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
is already an interesting calculation in this case.
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
is already an interesting calculation in this case.
Let
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
act as
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
act as
![]() $\sigma :\zeta _a \mapsto \zeta _a^s$
, where
$\sigma :\zeta _a \mapsto \zeta _a^s$
, where
![]() $s\in \mathbb {N}$
is coprime to a. Although it is sufficient to only consider
$s\in \mathbb {N}$
is coprime to a. Although it is sufficient to only consider
![]() $s\in \{1,\dots ,a-1\}$
, it will be essential to allow more general positive exponents s in the description of the action of
$s\in \{1,\dots ,a-1\}$
, it will be essential to allow more general positive exponents s in the description of the action of
![]() $\sigma $
on different roots of unity when we begin considering (normal reflection) subgroups of G shortly. We compute the identity of Theorem 1.1 in this example:
$\sigma $
on different roots of unity when we begin considering (normal reflection) subgroups of G shortly. We compute the identity of Theorem 1.1 in this example:
 $$ \begin{align*} \sum_{g \in G} \left(\prod_{\lambda_1(g) \neq 1} \frac{1-\lambda_1(g)^\sigma}{1-\lambda_1(g)}\right) q^{{\mathrm{fix}}_{V} (g)} &= q+\sum_{k=1}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k} = q+\sum_{k=1}^{a-1} \sum_{j=0}^{s-1} \zeta_a^{kj}\\ &= q+ \left(\sum_{j=0}^{s-1}\sum_{k=0}^{a-1} \zeta_a^{kj}\right)-s \\& = q+ \left(\sum_{j=0}^{s-1}\begin{cases} a & \text{if } a\,|\,j \\ 0 & \text{ otherwise} \end{cases}\right)-s \\ &= q+a\left\lceil \frac{s}{a} \right\rceil-s. \end{align*} $$
$$ \begin{align*} \sum_{g \in G} \left(\prod_{\lambda_1(g) \neq 1} \frac{1-\lambda_1(g)^\sigma}{1-\lambda_1(g)}\right) q^{{\mathrm{fix}}_{V} (g)} &= q+\sum_{k=1}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k} = q+\sum_{k=1}^{a-1} \sum_{j=0}^{s-1} \zeta_a^{kj}\\ &= q+ \left(\sum_{j=0}^{s-1}\sum_{k=0}^{a-1} \zeta_a^{kj}\right)-s \\& = q+ \left(\sum_{j=0}^{s-1}\begin{cases} a & \text{if } a\,|\,j \\ 0 & \text{ otherwise} \end{cases}\right)-s \\ &= q+a\left\lceil \frac{s}{a} \right\rceil-s. \end{align*} $$
On the other hand, we verify that
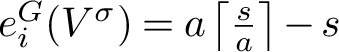 $e_i^G({V^\sigma }) =a\left \lceil \frac {s}{a} \right \rceil - s$
by exhibiting
$e_i^G({V^\sigma }) =a\left \lceil \frac {s}{a} \right \rceil - s$
by exhibiting
 $x^{a\left \lceil \frac {s}{a}\right \rceil -s} \otimes x^\sigma $
as a basis vector for the dual
$x^{a\left \lceil \frac {s}{a}\right \rceil -s} \otimes x^\sigma $
as a basis vector for the dual
![]() ${(U^G_\sigma )^*}$
of the Orlik-Solomon space
${(U^G_\sigma )^*}$
of the Orlik-Solomon space
![]() ${U^G_\sigma }$
, where x and
${U^G_\sigma }$
, where x and
![]() $x^\sigma $
denote basis vectors for
$x^\sigma $
denote basis vectors for
![]() ${V^*}$
and
${V^*}$
and
![]() ${(V^\sigma )^*}\!\!$
, respectively. More generally, we have the following.
${(V^\sigma )^*}\!\!$
, respectively. More generally, we have the following.
Lemma 7.1. For
![]() $G=C_a=\langle c\rangle $
the cyclic group of order a acting on its reflection representation
$G=C_a=\langle c\rangle $
the cyclic group of order a acting on its reflection representation
![]() $V=\mathbb {C}$
by
$V=\mathbb {C}$
by
![]() $c\mapsto \zeta _a^{-1}$
, and for any
$c\mapsto \zeta _a^{-1}$
, and for any
![]() $s\in \mathbb {Z}$
(not necessarily coprime to a), the
$s\in \mathbb {Z}$
(not necessarily coprime to a), the
![]() $V^{\otimes s}$
-exponent of G is
$V^{\otimes s}$
-exponent of G is
 $e_1^G(V^{\otimes s})=a\left \lceil \frac {s}{a} \right \rceil - s$
.
$e_1^G(V^{\otimes s})=a\left \lceil \frac {s}{a} \right \rceil - s$
.
Proof. Note that
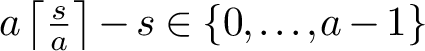 $a\left \lceil \frac {s}{a} \right \rceil - s\in \{0,\dots ,a-1\}$
is congruent to
$a\left \lceil \frac {s}{a} \right \rceil - s\in \{0,\dots ,a-1\}$
is congruent to
![]() $-s ({\text {mod }} a)$
. Letting
$-s ({\text {mod }} a)$
. Letting
![]() $x^s$
denote a basis vector for
$x^s$
denote a basis vector for
![]() $(V^{\otimes s})^*$
, we see that
$(V^{\otimes s})^*$
, we see that
![]() $c(x^s)=\zeta _a^sx^s$
and therefore
$c(x^s)=\zeta _a^sx^s$
and therefore
 $x^{a\left \lceil \frac {s}{a} \right \rceil - s}\otimes x^s$
is a basis vector for
$x^{a\left \lceil \frac {s}{a} \right \rceil - s}\otimes x^s$
is a basis vector for
 $(U_{V^{\otimes s}}^G)^*=({\mathcal {C}_G}\otimes (V^{\otimes s})^*)^G$
, because
$(U_{V^{\otimes s}}^G)^*=({\mathcal {C}_G}\otimes (V^{\otimes s})^*)^G$
, because
![]() ${\mathcal {C}_G}={\mathrm {span}}_{\mathbb {C}}\{1,x,\dots ,x^{a-1}\}$
in this case.
${\mathcal {C}_G}={\mathrm {span}}_{\mathbb {C}}\{1,x,\dots ,x^{a-1}\}$
in this case.
Suppose now that
![]() $a=de$
and consider
$a=de$
and consider
![]() $N=\langle c^e\rangle \simeq C_d$
, which is a normal reflection subgroup of G with quotient
$N=\langle c^e\rangle \simeq C_d$
, which is a normal reflection subgroup of G with quotient
![]() $H=G/N \simeq C_e$
. We denote by
$H=G/N \simeq C_e$
. We denote by
![]() $\zeta _d:=\zeta _a^e$
and
$\zeta _d:=\zeta _a^e$
and
![]() $\zeta _e:=\zeta _a^d$
, so that N acts on
$\zeta _e:=\zeta _a^d$
, so that N acts on
![]() $V^*$
via
$V^*$
via
![]() $c^e\mapsto \zeta _d$
and
$c^e\mapsto \zeta _d$
and
![]() $H=\langle cN\rangle $
acts on
$H=\langle cN\rangle $
acts on
![]() ${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^d\}$
via
${E^*}={\mathrm {span}}_{\mathbb {C}}\{x^d\}$
via
![]() $(cN)(x^d)=\zeta _e x^d$
.
$(cN)(x^d)=\zeta _e x^d$
.
Taking again
![]() $s\in \mathbb {N}$
coprime to a and letting
$s\in \mathbb {N}$
coprime to a and letting
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
be given by
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _a)/\mathbb {Q})$
be given by
![]() $\sigma : \zeta _a \mapsto \zeta _a^s$
, we have that
$\sigma : \zeta _a \mapsto \zeta _a^s$
, we have that
![]() ${E^\sigma }$
is the 1-dimensional representation of G defined by
${E^\sigma }$
is the 1-dimensional representation of G defined by
![]() $c\mapsto \zeta _a^{-ds}$
or, equivalently, the 1-dimensional representation of H defined by
$c\mapsto \zeta _a^{-ds}$
or, equivalently, the 1-dimensional representation of H defined by
![]() $cN\mapsto \zeta _e^{-s}$
. Therefore, by Lemma 7.1,
$cN\mapsto \zeta _e^{-s}$
. Therefore, by Lemma 7.1,
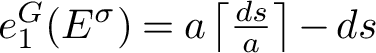 $e_1^G({E^\sigma })=a\left \lceil \frac {ds}{a}\right \rceil -ds$
and
$e_1^G({E^\sigma })=a\left \lceil \frac {ds}{a}\right \rceil -ds$
and
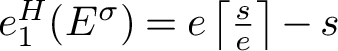 $e_1^H({E^\sigma })=e\left \lceil \frac {s}{e}\right \rceil -s$
. On the other hand,
$e_1^H({E^\sigma })=e\left \lceil \frac {s}{e}\right \rceil -s$
. On the other hand,
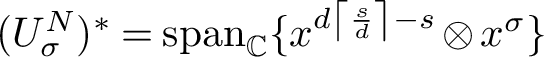 $({U^N_\sigma })^* = {\mathrm {span}}_{\mathbb {C}}\{ x^{d\left \lceil \frac {s}{d}\right \rceil -s} \otimes x^\sigma \}$
by Lemma 7.1, where again x and
$({U^N_\sigma })^* = {\mathrm {span}}_{\mathbb {C}}\{ x^{d\left \lceil \frac {s}{d}\right \rceil -s} \otimes x^\sigma \}$
by Lemma 7.1, where again x and
![]() $x^\sigma $
denote basis vectors for
$x^\sigma $
denote basis vectors for
![]() ${V^*}$
and
${V^*}$
and
![]() ${(V^\sigma )^*}$
, respectively. Hence, the generator c of G that acts by
${(V^\sigma )^*}$
, respectively. Hence, the generator c of G that acts by
![]() $\zeta _a^{-1}$
on its reflection representation V now acts by
$\zeta _a^{-1}$
on its reflection representation V now acts by
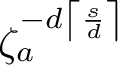 $\zeta _{a}^{-d\left \lceil \frac {s}{d}\right \rceil }$
on
$\zeta _{a}^{-d\left \lceil \frac {s}{d}\right \rceil }$
on
![]() ${U^N_\sigma }$
and therefore another application of Lemma 7.1 yields
${U^N_\sigma }$
and therefore another application of Lemma 7.1 yields
 $$ \begin{align*}e_1^G({U^N_\sigma})=a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil.\end{align*} $$
$$ \begin{align*}e_1^G({U^N_\sigma})=a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil.\end{align*} $$
When
![]() $s=1$
, we see that
$s=1$
, we see that
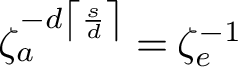 $\zeta _{a}^{-d\left \lceil \frac {s}{d}\right \rceil } = \zeta _e^{-1}$
, so that
$\zeta _{a}^{-d\left \lceil \frac {s}{d}\right \rceil } = \zeta _e^{-1}$
, so that
![]() ${U^N} \simeq {E}$
is the reflection representation of
${U^N} \simeq {E}$
is the reflection representation of
![]() $H=C_e$
defined by
$H=C_e$
defined by
![]() $cN\mapsto \zeta _e^{-1}$
. But because
$cN\mapsto \zeta _e^{-1}$
. But because
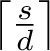 $\left \lceil \frac {s}{d}\right \rceil $
is not necessarily coprime to e, even when
$\left \lceil \frac {s}{d}\right \rceil $
is not necessarily coprime to e, even when
![]() $s\in \{1,\dots ,a-1\}$
, it is possible for the action of H on
$s\in \{1,\dots ,a-1\}$
, it is possible for the action of H on
![]() ${U^N_\sigma }$
to fail to be faithful; for example, when
${U^N_\sigma }$
to fail to be faithful; for example, when
![]() $s=a-1$
corresponding to
$s=a-1$
corresponding to
![]() $\sigma $
acting by complex conjugation, the generator c of G acts trivially on
$\sigma $
acting by complex conjugation, the generator c of G acts trivially on
![]() ${(U^N_\sigma )^*}$
by
${(U^N_\sigma )^*}$
by
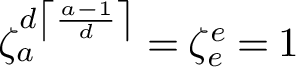 $\zeta _a^{d\left \lceil \frac {a-1}{d}\right \rceil }=\zeta _e^{e}=1$
. Hence, we see that, as we mentioned in Remark 4.4 and contrary to what one might have hoped based on the
$\zeta _a^{d\left \lceil \frac {a-1}{d}\right \rceil }=\zeta _e^{e}=1$
. Hence, we see that, as we mentioned in Remark 4.4 and contrary to what one might have hoped based on the
![]() $s=1$
case, in general
$s=1$
case, in general
![]() ${U^N_\sigma } \not \simeq {E}^\sigma $
as G-representations.
${U^N_\sigma } \not \simeq {E}^\sigma $
as G-representations.
Using the explicit descriptions of the actions of N and G on
![]() ${V^\sigma }$
and the actions of G and H on
${V^\sigma }$
and the actions of G and H on
![]() ${U^N_\sigma }$
and
${U^N_\sigma }$
and
![]() ${E^\sigma }$
described above, the three equalities in Theorem 1.3 become the following numerological statements.
${E^\sigma }$
described above, the three equalities in Theorem 1.3 become the following numerological statements.
Corollary 7.2. Let
![]() $a=de$
and
$a=de$
and
![]() $s\in \mathbb {N}$
be coprime to a. Then
$s\in \mathbb {N}$
be coprime to a. Then
 $$ \begin{align*} \left(d\left\lceil \frac{s}{d}\right\rceil -s\right) +\left(a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil\right) &= \left(a \left\lceil \frac{s}{a}\right\rceil - s\right);\\ d\cdot \left(e\left\lceil\frac{s}{e}\right\rceil-s\right) &= \left(a\left\lceil\frac{ds}{a}\right\rceil-ds\right);\\ d\cdot e &= a. \end{align*} $$
$$ \begin{align*} \left(d\left\lceil \frac{s}{d}\right\rceil -s\right) +\left(a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil\right) &= \left(a \left\lceil \frac{s}{a}\right\rceil - s\right);\\ d\cdot \left(e\left\lceil\frac{s}{e}\right\rceil-s\right) &= \left(a\left\lceil\frac{ds}{a}\right\rceil-ds\right);\\ d\cdot e &= a. \end{align*} $$
The first (and only nontrivial) equality in this case is equivalent to the identity
 $\left \lceil \frac {\left \lceil \frac {s}{d}\right \rceil }{e}\right \rceil =\left \lceil \frac {s}{de}\right \rceil $
, which holds more generally for
$\left \lceil \frac {\left \lceil \frac {s}{d}\right \rceil }{e}\right \rceil =\left \lceil \frac {s}{de}\right \rceil $
, which holds more generally for
![]() $e \in \mathbb {N}$
and
$e \in \mathbb {N}$
and
![]() $s,d \in \mathbb {R}$
.
$s,d \in \mathbb {R}$
.
Our Theorem 1.4 in this situation states that the following expressions are equal:
 $$ \begin{align*}\sum_{g \in G} \left(\prod_{\lambda_1(g)\neq 1}\!\!\!\frac{1-\lambda_1(g)^s}{1-\lambda_1(g)}\right)\! q^{{\mathrm{fix}}_V (g)}t^{{\mathrm{fix}}_E (g)} &= qt+\left(\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}\right)\!t+\left(\sum_{\substack{ k=1\\ e\, \nmid \, k}}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k}\right)\\[-0.2pt] \left(qt+e_1^N({V^\sigma})t+e_1^G({U^N_\sigma})\right)&= qt+\left(d \left\lceil\frac{s}{d}\right\rceil -s\right)t+\left(a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil\right) .\end{align*} $$
$$ \begin{align*}\sum_{g \in G} \left(\prod_{\lambda_1(g)\neq 1}\!\!\!\frac{1-\lambda_1(g)^s}{1-\lambda_1(g)}\right)\! q^{{\mathrm{fix}}_V (g)}t^{{\mathrm{fix}}_E (g)} &= qt+\left(\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}\right)\!t+\left(\sum_{\substack{ k=1\\ e\, \nmid \, k}}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k}\right)\\[-0.2pt] \left(qt+e_1^N({V^\sigma})t+e_1^G({U^N_\sigma})\right)&= qt+\left(d \left\lceil\frac{s}{d}\right\rceil -s\right)t+\left(a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil\right) .\end{align*} $$
The equality of the coefficients of t
 $$ \begin{align*}\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}=d\left\lceil\frac{s}{d}\right\rceil-s =e_1^N({V^\sigma})\end{align*} $$
$$ \begin{align*}\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}=d\left\lceil\frac{s}{d}\right\rceil-s =e_1^N({V^\sigma})\end{align*} $$
was already verified above with a in place of d. To verify the equality of constant terms
 $$ \begin{align*}\sum_{\substack{ k=1\\ e\, \nmid \, k}}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k}=a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil,\end{align*} $$
$$ \begin{align*}\sum_{\substack{ k=1\\ e\, \nmid \, k}}^{a-1} \frac{1-\zeta_a^{ks}}{1-\zeta_a^k}=a\left\lceil\frac{\left\lceil\frac{s}{d}\right\rceil}{e}\right\rceil-d\left\lceil \frac{s}{d}\right\rceil,\end{align*} $$
one could proceed, for example, by noting that the same arguments show that the left-hand side is equal to
 $$ \begin{align*}\left(\sum_{k=1}^{a-1}\frac{1-\zeta_a^{ks}}{1-\zeta_a^{k}}\right)-\left(\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}\right)=\left(a\left\lceil\frac{s}{a}\right\rceil-s \right)-\left(d\left\lceil\frac{s}{d}\right\rceil-s\right)=a\left\lceil\frac{s}{a}\right\rceil -d\left\lceil\frac{s}{d}\right\rceil\end{align*} $$
$$ \begin{align*}\left(\sum_{k=1}^{a-1}\frac{1-\zeta_a^{ks}}{1-\zeta_a^{k}}\right)-\left(\sum_{j=1}^{d-1}\frac{1-\zeta_d^{js}}{1-\zeta_d^{j}}\right)=\left(a\left\lceil\frac{s}{a}\right\rceil-s \right)-\left(d\left\lceil\frac{s}{d}\right\rceil-s\right)=a\left\lceil\frac{s}{a}\right\rceil -d\left\lceil\frac{s}{d}\right\rceil\end{align*} $$
and then appealing either to Corollary 7.2 or to more general properties of ceilings to obtain the equality
 $\left \lceil \frac {\left \lceil \frac {s}{d}\right \rceil }{e}\right \rceil =\left \lceil \frac {s}{a}\right \rceil $
.
$\left \lceil \frac {\left \lceil \frac {s}{d}\right \rceil }{e}\right \rceil =\left \lceil \frac {s}{a}\right \rceil $
.
We conclude our discussion of the cyclic case with a concrete illustration of the subtlety involved in proving (in Corollary 4.11) that the sum side of Theorem 1.4 provides the correct contribution coset by coset but not term by term as in the proof of Theorem 1.1.
To compare the two situations, we compute the trace of
![]() $ng=c^{ek}\cdot c^j\in Ng$
(for
$ng=c^{ek}\cdot c^j\in Ng$
(for
![]() $0 \leq k < d$
and
$0 \leq k < d$
and
![]() $0 \leq j < e$
) acting on
$0 \leq j < e$
) acting on
![]() $S(V^*) \otimes \bigwedge (V^\sigma )^*$
and
$S(V^*) \otimes \bigwedge (V^\sigma )^*$
and
![]() $S(V^*) \otimes \bigwedge ({U^N_\sigma })^*$
:
$S(V^*) \otimes \bigwedge ({U^N_\sigma })^*$
:
 $$ \begin{align*} \sum_{\ell,p\geq 0}\mathrm{tr}\left((ng) | S(V^*)_\ell \otimes {\textstyle \bigwedge^p}(V^\sigma)^*\right)x^\ell u^p &=\frac{1+u (c^{ek+j})|_{(V^\sigma)^*}}{1-x(c^{ek+j})|_{(V)^*}}\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ &= \frac{1+u \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ &=\left(\frac{1- \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}+\frac{q(1-x) \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}\right)\Bigg|_{x \to 1}\\ &=\left(\prod_{\lambda_1(ng)\neq 1} \frac{1-\lambda_1(ng)^\sigma}{1-\lambda_1(ng)} \right)q^{{\mathrm{fix}}_V(ng)}, \end{align*} $$
$$ \begin{align*} \sum_{\ell,p\geq 0}\mathrm{tr}\left((ng) | S(V^*)_\ell \otimes {\textstyle \bigwedge^p}(V^\sigma)^*\right)x^\ell u^p &=\frac{1+u (c^{ek+j})|_{(V^\sigma)^*}}{1-x(c^{ek+j})|_{(V)^*}}\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ &= \frac{1+u \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}\Bigg|_{\substack{u=q(1-x)-1\\ x \to 1}}\\ &=\left(\frac{1- \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}+\frac{q(1-x) \zeta_a^{s(ek+j)}}{1-x\zeta_a^{ek+j}}\right)\Bigg|_{x \to 1}\\ &=\left(\prod_{\lambda_1(ng)\neq 1} \frac{1-\lambda_1(ng)^\sigma}{1-\lambda_1(ng)} \right)q^{{\mathrm{fix}}_V(ng)}, \end{align*} $$
because the term
 $\frac {q(1-x) \zeta _a^{s(ek+j)}}{1-x\zeta _a^{ek+j}}$
vanishes in the limit
$\frac {q(1-x) \zeta _a^{s(ek+j)}}{1-x\zeta _a^{ek+j}}$
vanishes in the limit
![]() $x \to 1$
for all elements of G except the identity. For example, for
$x \to 1$
for all elements of G except the identity. For example, for
![]() $a=6, d=2, e=3$
and
$a=6, d=2, e=3$
and
![]() $s=5$
, summing over all elements of
$s=5$
, summing over all elements of
![]() $C_6=\langle c \rangle $
and then specialising
$C_6=\langle c \rangle $
and then specialising
![]() $u\mapsto q(1-x)-1$
and taking the limit as
$u\mapsto q(1-x)-1$
and taking the limit as
![]() $x \to 1$
gives
$x \to 1$
gives

so that each element contributes the ‘correct amount’ specified by the sum side of Theorem 1.1.
On the other hand, computing the sum side of our refinement Theorem 1.4 gives the following, where we have written
 $b:=e_1^N({V^\sigma })=d\left \lceil \frac {s}{d}\right \rceil -s$
for legibility:
$b:=e_1^N({V^\sigma })=d\left \lceil \frac {s}{d}\right \rceil -s$
for legibility:
 $$ \begin{align*} \sum_{\ell,p\geq 0}\!\!\mathrm{tr}\left((ng) | S(V^*)_\ell \otimes \textstyle\bigwedge^p{(U^N_\sigma)^*}\right)x^\ell y^{bp}u^p &= \frac{1+u y^b (c^{ek+j})|_{{(U^N_\sigma)^*}_{\!\!\!b}}}{1-x(c^{ek+j})|_{(V)^*}}\Bigg|_{\substack{y=x^t \\ u=qt(1-x)-1\\ x \to 1}}\\ &= \frac{1+ux^{tb} \zeta_e^{\left\lceil \frac{s}{d}\right\rceil(ek+j)}}{1-x\zeta_a^{ek+j}}\Bigg|_{\substack{u=qt(1-x)-1\\ x \to 1}}\\ &= \Biggl(\frac{1- x^{tb} \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-x\zeta_a^{ek+j}}+\frac{x^{tb} qt (1-x) \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-x\zeta_a^{ek+j}}\Biggr)\Bigg|_{x \to 1}\\ &= \begin{cases} qt+bt& \text{if } k=j=0\\ \frac{1- \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-\zeta_a^{ek+j}} & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{\ell,p\geq 0}\!\!\mathrm{tr}\left((ng) | S(V^*)_\ell \otimes \textstyle\bigwedge^p{(U^N_\sigma)^*}\right)x^\ell y^{bp}u^p &= \frac{1+u y^b (c^{ek+j})|_{{(U^N_\sigma)^*}_{\!\!\!b}}}{1-x(c^{ek+j})|_{(V)^*}}\Bigg|_{\substack{y=x^t \\ u=qt(1-x)-1\\ x \to 1}}\\ &= \frac{1+ux^{tb} \zeta_e^{\left\lceil \frac{s}{d}\right\rceil(ek+j)}}{1-x\zeta_a^{ek+j}}\Bigg|_{\substack{u=qt(1-x)-1\\ x \to 1}}\\ &= \Biggl(\frac{1- x^{tb} \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-x\zeta_a^{ek+j}}+\frac{x^{tb} qt (1-x) \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-x\zeta_a^{ek+j}}\Biggr)\Bigg|_{x \to 1}\\ &= \begin{cases} qt+bt& \text{if } k=j=0\\ \frac{1- \zeta_e^{j\left\lceil \frac{s}{d}\right\rceil}}{1-\zeta_a^{ek+j}} & \text{ otherwise}. \end{cases} \end{align*} $$
Continuing the example with
![]() $a=6, d=2, e=3$
and
$a=6, d=2, e=3$
and
![]() $s=5$
, because
$s=5$
, because
![]() $\lceil \frac {s}{d}\rceil =e=3$
, after specialising
$\lceil \frac {s}{d}\rceil =e=3$
, after specialising
![]() $y\mapsto x^t$
,
$y\mapsto x^t$
,
![]() $u\mapsto qt(1-x)-1$
, and taking the limit as
$u\mapsto qt(1-x)-1$
, and taking the limit as
![]() $x\to 1$
, every term except for the identity vanishes – in particular, each element of G does not contribute the ‘correct amount’ specified by the sum side of Theorem 1.4:
$x\to 1$
, every term except for the identity vanishes – in particular, each element of G does not contribute the ‘correct amount’ specified by the sum side of Theorem 1.4:

Here the only coset that provides a nontrivial contribution to the sum side of Theorem 1.4 is the trivial coset N, as predicted by the computation of the sum side of Theorem 1.1, but this nontrivial contribution of
![]() $qt+t$
for the whole coset N is concentrated on the identity element
$qt+t$
for the whole coset N is concentrated on the identity element
![]() $c^0\in N$
alone, which, according to the sum side of Theorem 1.4, should have only contributed
$c^0\in N$
alone, which, according to the sum side of Theorem 1.4, should have only contributed
![]() $qt$
, whereas the nontrivial element
$qt$
, whereas the nontrivial element
![]() $c^3\in N$
did not provide the correct contribution of
$c^3\in N$
did not provide the correct contribution of
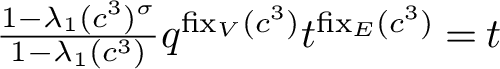 $\frac {1-\lambda _1(c^3)^\sigma }{1-\lambda _1(c^3)}q^{{\mathrm {fix}}_V(c^3)}t^{{\mathrm {fix}}_{E}(c^3)}=t$
specified by the sum side of Theorem 1.4.
$\frac {1-\lambda _1(c^3)^\sigma }{1-\lambda _1(c^3)}q^{{\mathrm {fix}}_V(c^3)}t^{{\mathrm {fix}}_{E}(c^3)}=t$
specified by the sum side of Theorem 1.4.
7.2 The Infinite Family
 $G(ab,b,r)$
$G(ab,b,r)$
We begin by defining an ad hoc operation on G-modules for
![]() $G=G(ab,b,r)$
(whose definition was given in Section 6) that will allow us to succintly identify the Orlik-Solomon spaces
$G=G(ab,b,r)$
(whose definition was given in Section 6) that will allow us to succintly identify the Orlik-Solomon spaces
![]() ${U^N_\sigma }$
of Definition 2.9 for the two kinds of normal reflection subgroups N of G listed in Theorem 6.1 that occur in all ranks
${U^N_\sigma }$
of Definition 2.9 for the two kinds of normal reflection subgroups N of G listed in Theorem 6.1 that occur in all ranks
![]() $r\geq 2$
.
$r\geq 2$
.
Definition 7.3. For
![]() $n\in \mathbb {Z}$
, let
$n\in \mathbb {Z}$
, let
![]() $\mu _n:G\rightarrow G$
be the group endomorphism obtained by raising each nonzero matrix entry to the nth power. Given any representation
$\mu _n:G\rightarrow G$
be the group endomorphism obtained by raising each nonzero matrix entry to the nth power. Given any representation
![]() $\rho :G\rightarrow \mathrm {GL}(W)$
, we define the fake tensor power
$\rho :G\rightarrow \mathrm {GL}(W)$
, we define the fake tensor power
![]() $W^{\boxtimes n}$
as the representation
$W^{\boxtimes n}$
as the representation
![]() $\rho \circ \mu _n:G\rightarrow \mathrm {GL}(W)$
.
$\rho \circ \mu _n:G\rightarrow \mathrm {GL}(W)$
.
Remark 7.4. Note that in general the ‘fake nth power map’
![]() $\mu _n$
used in Definition 7.3 will be neither injective nor surjective when
$\mu _n$
used in Definition 7.3 will be neither injective nor surjective when
![]() $\mathrm {gcd}(ab,n)\neq 1$
. In the case where
$\mathrm {gcd}(ab,n)\neq 1$
. In the case where
![]() $\mathrm {gcd}(ab,s)=1$
, note that
$\mathrm {gcd}(ab,s)=1$
, note that
![]() $V^{\boxtimes s}\simeq V^\sigma $
, the Galois twist corresponding to
$V^{\boxtimes s}\simeq V^\sigma $
, the Galois twist corresponding to
![]() $\sigma :\zeta _{ab}\mapsto \zeta _{ab}^s$
.
$\sigma :\zeta _{ab}\mapsto \zeta _{ab}^s$
.
Although the fake tensor power operation could be expressed in terms of more systematic constructions (interpreting
![]() $G(ab,b,r)$
as an index-b subgroup of the wreath product
$G(ab,b,r)$
as an index-b subgroup of the wreath product
![]() $C_{ab}\wr S_r$
), we have preferred our ad hoc definition for its simplicity and concreteness.
$C_{ab}\wr S_r$
), we have preferred our ad hoc definition for its simplicity and concreteness.
In the following result, we identify the G-module
![]() ${U^N_\sigma }$
when
${U^N_\sigma }$
when
![]() $N=C_d^r$
as in Theorem 6.1(r.a) for
$N=C_d^r$
as in Theorem 6.1(r.a) for
![]() $r\geq 2$
.
$r\geq 2$
.
Proposition 7.5. Let
![]() $a=de$
and
$a=de$
and
![]() $N=C_d^r\triangleleft G(ab,b,r)=G$
and fix
$N=C_d^r\triangleleft G(ab,b,r)=G$
and fix
![]() $\sigma : \zeta _{ab} \to \zeta _{ab}^s$
for
$\sigma : \zeta _{ab} \to \zeta _{ab}^s$
for
![]() $1 \leq s < ab$
with
$1 \leq s < ab$
with
![]() $\gcd (s,ab)=1$
. Then
$\gcd (s,ab)=1$
. Then
![]() $H\simeq G(eb,b,r)$
and
$H\simeq G(eb,b,r)$
and
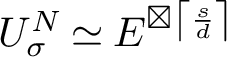 ${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{d}\right \rceil }$
as G-modules.
${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{d}\right \rceil }$
as G-modules.
Proof. For this choice of N, the fundamental N-invariants are
![]() ${N}_i = x_i^d$
for
${N}_i = x_i^d$
for
![]() $1 \leq i \leq r$
, and we obtain the basis
$1 \leq i \leq r$
, and we obtain the basis
 $u_i^N= x_i^{d\left \lceil \frac {s}{d}\right \rceil -s} \otimes x_i^\sigma $
for
$u_i^N= x_i^{d\left \lceil \frac {s}{d}\right \rceil -s} \otimes x_i^\sigma $
for
![]() ${(U^N_\sigma )^*}$
as in Section 7.1.
${(U^N_\sigma )^*}$
as in Section 7.1.
Fix
![]() $g\in G$
and
$g\in G$
and
![]() $\ell \in \{1,\dots ,r\}$
and suppose that
$\ell \in \{1,\dots ,r\}$
and suppose that
![]() $g(x_\ell )=\zeta _{ab}^k x_j$
for some
$g(x_\ell )=\zeta _{ab}^k x_j$
for some
![]() $0\leq k<ab$
and
$0\leq k<ab$
and
![]() $j\in \{1,\dots ,r\}$
. Then from the explicit descriptions of
$j\in \{1,\dots ,r\}$
. Then from the explicit descriptions of
![]() ${E^*}$
and
${E^*}$
and
![]() ${(U^N_\sigma )^*}$
above we see that
${(U^N_\sigma )^*}$
above we see that
![]() $g({N}_\ell )=\zeta _{ab}^{kd}{N}_j$
and
$g({N}_\ell )=\zeta _{ab}^{kd}{N}_j$
and
 $g(u_{\ell }^N)=\zeta _{ab}^{kd\left \lceil \frac {s}{d}\right \rceil }u_j^N$
. It follows that
$g(u_{\ell }^N)=\zeta _{ab}^{kd\left \lceil \frac {s}{d}\right \rceil }u_j^N$
. It follows that
![]() ${E}\simeq V^{\boxtimes d}$
and
${E}\simeq V^{\boxtimes d}$
and
 ${U^N_\sigma }\simeq V^{\boxtimes d\left \lceil \frac {s}{d}\right \rceil }$
, and therefore
${U^N_\sigma }\simeq V^{\boxtimes d\left \lceil \frac {s}{d}\right \rceil }$
, and therefore
 ${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{d}\right \rceil }$
, as claimed.
${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{d}\right \rceil }$
, as claimed.
As a special case of Proposition 7.5,
![]() ${U^N_\sigma }\simeq {E}$
when
${U^N_\sigma }\simeq {E}$
when
![]() $N=C_d^r$
and
$N=C_d^r$
and
![]() $s<d$
.
$s<d$
.
Following [Reference Reiner and Shepler18, Proposition 14.1], a simple choice of invariant polynomials for
![]() $G(ab,b,r)$
is the set
$G(ab,b,r)$
is the set
 $$ \begin{align} G_i=\sum_{j=1}^r x_j^{abi} \quad\text{for}\ 1 \leq i < r \qquad\text{and}\qquad G_r = (x_1 \cdots x_r)^a. \end{align} $$
$$ \begin{align} G_i=\sum_{j=1}^r x_j^{abi} \quad\text{for}\ 1 \leq i < r \qquad\text{and}\qquad G_r = (x_1 \cdots x_r)^a. \end{align} $$
In the following result we determine the Orlik-Solomon space
![]() ${U^G_\sigma }$
of Definition 2.9 up to graded cryptomorphism.
${U^G_\sigma }$
of Definition 2.9 up to graded cryptomorphism.
Theorem 7.6. Let
![]() $G=G(ab,b,r)$
and
$G=G(ab,b,r)$
and
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _{ab})/\mathbb {Q})$
be given by
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\zeta _{ab})/\mathbb {Q})$
be given by
![]() $\sigma (\zeta _{ab})=\zeta _{ab}^s$
for
$\sigma (\zeta _{ab})=\zeta _{ab}^s$
for
![]() $1 \leq s < ab$
with
$1 \leq s < ab$
with
![]() $\gcd (s,ab)=1$
. Let
$\gcd (s,ab)=1$
. Let
 ${(\tilde {U}^G_\sigma )^*}:={\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1^G,\dots ,\tilde {u}_r^G\}$
, where
${(\tilde {U}^G_\sigma )^*}:={\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1^G,\dots ,\tilde {u}_r^G\}$
, where
 $$ \begin{align*}\tilde{u}_i^G = \sum_{j=1}^r x_j^{abi-s}\otimes x_j^\sigma \quad \text{for}\ \ 1 \leq i < r \qquad \text{and}\qquad \tilde{u}_r^G = \sum_{j=1}^r (x_1 \cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a} x_j^{-s} \otimes x_j^\sigma.\end{align*} $$
$$ \begin{align*}\tilde{u}_i^G = \sum_{j=1}^r x_j^{abi-s}\otimes x_j^\sigma \quad \text{for}\ \ 1 \leq i < r \qquad \text{and}\qquad \tilde{u}_r^G = \sum_{j=1}^r (x_1 \cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a} x_j^{-s} \otimes x_j^\sigma.\end{align*} $$
Let
![]() $\eta _G:S(V^*)\rightarrow {\mathcal {C}_G}$
denote the natural projection from
$\eta _G:S(V^*)\rightarrow {\mathcal {C}_G}$
denote the natural projection from
![]() $S(V^*)$
onto its G-stable direct summand
$S(V^*)$
onto its G-stable direct summand
![]() ${\mathcal {C}_G}$
. Then
${\mathcal {C}_G}$
. Then
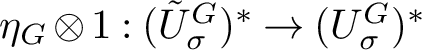 $\eta _G\otimes 1:{(\tilde {U}^G_\sigma )^*}\rightarrow {(U^G_\sigma )^*}$
is an isomorphism of graded vector spaces, and therefore the
$\eta _G\otimes 1:{(\tilde {U}^G_\sigma )^*}\rightarrow {(U^G_\sigma )^*}$
is an isomorphism of graded vector spaces, and therefore the
![]() ${V^\sigma }$
-exponents of
${V^\sigma }$
-exponents of
![]() $G(ab,b,r)$
are
$G(ab,b,r)$
are
 $$ \begin{align*}\left\{ab-s,2ab-s,\ldots,(r{-}1)ab-s,\left\lceil \frac{s}{a}\right\rceil ar-s\right\}.\end{align*} $$
$$ \begin{align*}\left\{ab-s,2ab-s,\ldots,(r{-}1)ab-s,\left\lceil \frac{s}{a}\right\rceil ar-s\right\}.\end{align*} $$
Proof. By Lemma 3.6 (applied in the special case where
![]() $N=G$
), it suffices to show that the
$N=G$
), it suffices to show that the
![]() $\tilde {u}_i^G$
form a basis for
$\tilde {u}_i^G$
form a basis for
![]() $(S(V^*)\otimes {(V^\sigma )^*})^G$
as a free
$(S(V^*)\otimes {(V^\sigma )^*})^G$
as a free
![]() $S(V^*)^G$
-module.
$S(V^*)^G$
-module.
Because the group
![]() $G(ab,b,r)$
acts on
$G(ab,b,r)$
acts on
![]() $V^*$
by permutation of the
$V^*$
by permutation of the
![]() $x_i$
and multiplication by
$x_i$
and multiplication by
![]() $(ab)$
th roots of unity, it is clear that the
$(ab)$
th roots of unity, it is clear that the
![]() $\tilde {u}_i^G\in S(V^*)\otimes {(V^\sigma )^*}$
are G-invariant. Let
$\tilde {u}_i^G\in S(V^*)\otimes {(V^\sigma )^*}$
are G-invariant. Let
 $u_i^G=\sum _{j=0}^ra_{ij}^G\otimes x_j^\sigma $
be a homogeneous basis for
$u_i^G=\sum _{j=0}^ra_{ij}^G\otimes x_j^\sigma $
be a homogeneous basis for
![]() ${(U^G_\sigma )^*}$
, where
${(U^G_\sigma )^*}$
, where
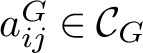 $a_{ij}^G\in {\mathcal {C}_G}$
and
$a_{ij}^G\in {\mathcal {C}_G}$
and
 $\mathrm {deg}(a_{ij}^G)=e_i^G({V^\sigma })$
whenever
$\mathrm {deg}(a_{ij}^G)=e_i^G({V^\sigma })$
whenever
 $a_{ij}^G\neq 0$
. Because
$a_{ij}^G\neq 0$
. Because
![]() $(S(V^*)\otimes {(V^\sigma )^*})^G\simeq S(V^*)^G\otimes {(U^G_\sigma )^*}$
, there exists a matrix
$(S(V^*)\otimes {(V^\sigma )^*})^G\simeq S(V^*)^G\otimes {(U^G_\sigma )^*}$
, there exists a matrix
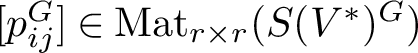 $[p_{ij}^G]\in \mathrm {Mat}_{r\times r}(S(V^*)^G)$
such that
$[p_{ij}^G]\in \mathrm {Mat}_{r\times r}(S(V^*)^G)$
such that
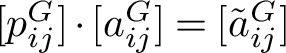 $[p_{ij}^G]\cdot [a_{ij}^G]=[\tilde {a}_{ij}^G]$
, where
$[p_{ij}^G]\cdot [a_{ij}^G]=[\tilde {a}_{ij}^G]$
, where
 $$ \begin{align*}\tilde{a}_{ij}^G = \begin{cases} x_j^{abi-s} & \text{ for } 1 \leq i <r \\ (x_1\cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a} x_j^{-s} & \text{ for } i=r\end{cases}\end{align*} $$
$$ \begin{align*}\tilde{a}_{ij}^G = \begin{cases} x_j^{abi-s} & \text{ for } 1 \leq i <r \\ (x_1\cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a} x_j^{-s} & \text{ for } i=r\end{cases}\end{align*} $$
or, equivalently, such that
 $\tilde {u}^G_i=\sum _{j=1}^rp_{ij}^G\cdot u_j^G$
. It is clear from the form of the
$\tilde {u}^G_i=\sum _{j=1}^rp_{ij}^G\cdot u_j^G$
. It is clear from the form of the
![]() $\tilde {u}_i^G$
that they are
$\tilde {u}_i^G$
that they are
![]() $\mathbb {C}$
-linearly independent, which implies that
$\mathbb {C}$
-linearly independent, which implies that
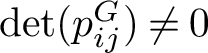 $\mathrm {det}(p_{ij}^G)\neq 0$
.
$\mathrm {det}(p_{ij}^G)\neq 0$
.
We claim that
 $$ \begin{align}\mathrm{det}(a_{ij}^G)=c\cdot (x_1\cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a-s} \prod_{1\leq i < j \leq r} (x_i^{ab}-x_j^{ab})\end{align} $$
$$ \begin{align}\mathrm{det}(a_{ij}^G)=c\cdot (x_1\cdots x_r)^{\left\lceil \frac{s}{a}\right\rceil a-s} \prod_{1\leq i < j \leq r} (x_i^{ab}-x_j^{ab})\end{align} $$
for some
![]() $0\neq c\in \mathbb {C}$
. By Gutkin’s theorem [Reference Lehrer and Taylor14, Theorem 10.13],
$0\neq c\in \mathbb {C}$
. By Gutkin’s theorem [Reference Lehrer and Taylor14, Theorem 10.13],
 $$ \begin{align*}\mathrm{det}(a_{ij}^G)=c\cdot \prod_{H\in\mathcal{R}_G} L_H^{C(H,{V^\sigma})}\end{align*} $$
$$ \begin{align*}\mathrm{det}(a_{ij}^G)=c\cdot \prod_{H\in\mathcal{R}_G} L_H^{C(H,{V^\sigma})}\end{align*} $$
for some
![]() $0\neq c\in \mathbb {C}$
, where
$0\neq c\in \mathbb {C}$
, where
![]() $\mathcal {R}_G$
denotes the set of reflecting hyperplanes for G,
$\mathcal {R}_G$
denotes the set of reflecting hyperplanes for G,
![]() $L_H\in V^*$
denotes a linear form defining H and
$L_H\in V^*$
denotes a linear form defining H and
![]() $C(H,{V^\sigma })$
is defined as follows. Denoting by
$C(H,{V^\sigma })$
is defined as follows. Denoting by
![]() $\langle r_H\rangle = G_H<G$
the cyclic subgroup of G that stabilises H pointwise, decompose
$\langle r_H\rangle = G_H<G$
the cyclic subgroup of G that stabilises H pointwise, decompose
 ${(V^\sigma )^*}\simeq \bigoplus _{i=1}^r\lambda ^{\otimes k_i}$
as a
${(V^\sigma )^*}\simeq \bigoplus _{i=1}^r\lambda ^{\otimes k_i}$
as a
![]() $G_H$
-module with
$G_H$
-module with
![]() $0\leq k_i<|G_H|$
for
$0\leq k_i<|G_H|$
for
![]() $1\leq i\leq r$
, where
$1\leq i\leq r$
, where
![]() $\lambda $
denotes the standard representation of
$\lambda $
denotes the standard representation of
![]() $G_H$
on the
$G_H$
on the
![]() $G_H$
-stable complement of H in V, and define
$G_H$
-stable complement of H in V, and define
![]() $C(H,{V^\sigma }):=\sum _{i=1}^r k_i$
. When
$C(H,{V^\sigma }):=\sum _{i=1}^r k_i$
. When
![]() $L_H=x_i-\zeta _{ab}^\ell x_j$
with
$L_H=x_i-\zeta _{ab}^\ell x_j$
with
![]() $i\neq j$
and
$i\neq j$
and
![]() $0\leq \ell <ab-1$
, the cyclic generator
$0\leq \ell <ab-1$
, the cyclic generator
![]() $r_H$
has order
$r_H$
has order
![]() $2$
and
$2$
and
![]() ${V^\sigma }\simeq \lambda \oplus \mathbb {C}^{\oplus (r-1)}$
as a
${V^\sigma }\simeq \lambda \oplus \mathbb {C}^{\oplus (r-1)}$
as a
![]() $G_H$
-module, and therefore
$G_H$
-module, and therefore
![]() $C(H,{V^\sigma })=1$
in this case. If
$C(H,{V^\sigma })=1$
in this case. If
![]() $a>1$
, then we have the additional reflecting hyperplanes defined by
$a>1$
, then we have the additional reflecting hyperplanes defined by
![]() $L_H=x_i$
; in this case, the cyclic generator
$L_H=x_i$
; in this case, the cyclic generator
![]() $r_H$
has order a and
$r_H$
has order a and
 ${(V^\sigma )^*}\simeq \lambda ^{\otimes \left (\left \lceil \frac {s}{a}\right \rceil a -s\right )}\oplus \mathbb {C}^{\oplus (r-1)}$
as a
${(V^\sigma )^*}\simeq \lambda ^{\otimes \left (\left \lceil \frac {s}{a}\right \rceil a -s\right )}\oplus \mathbb {C}^{\oplus (r-1)}$
as a
![]() $G_H$
-module (cf. Lemma 7.1), and therefore
$G_H$
-module (cf. Lemma 7.1), and therefore
 $C(H,{V^\sigma })=\left \lceil \frac {s}{a}\right \rceil a -s$
. This concludes the proof of Equation (15).
$C(H,{V^\sigma })=\left \lceil \frac {s}{a}\right \rceil a -s$
. This concludes the proof of Equation (15).
We see by direct inspection that
 $$ \begin{align*}\mathrm{deg}(\mathrm{det}(a_{ij}^G))=ab\cdot\binom{r}{2}+r\cdot\left(\left\lceil\frac{s}{a}\right\rceil a-s\right)=\mathrm{deg}(\mathrm{det}(\tilde{a}_{ij}^G)),\end{align*} $$
$$ \begin{align*}\mathrm{deg}(\mathrm{det}(a_{ij}^G))=ab\cdot\binom{r}{2}+r\cdot\left(\left\lceil\frac{s}{a}\right\rceil a-s\right)=\mathrm{deg}(\mathrm{det}(\tilde{a}_{ij}^G)),\end{align*} $$
which implies that
 $\mathrm {deg}(\mathrm {det}(p_{ij}^G))=0$
, and because
$\mathrm {deg}(\mathrm {det}(p_{ij}^G))=0$
, and because
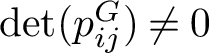 $\mathrm {det}(p_{ij}^G)\neq 0$
as we had already seen, it follows that
$\mathrm {det}(p_{ij}^G)\neq 0$
as we had already seen, it follows that
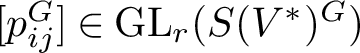 $[p_{ij}^G]\in \mathrm {GL}_r(S(V^*)^G)$
, as we wanted to show.
$[p_{ij}^G]\in \mathrm {GL}_r(S(V^*)^G)$
, as we wanted to show.
Remark 7.7. Note that when
![]() $s=ab-1$
, so that
$s=ab-1$
, so that
![]() $\sigma $
acts by complex conjugation, the basis
$\sigma $
acts by complex conjugation, the basis
![]() $\tilde {u_i}^G$
for
$\tilde {u_i}^G$
for
 ${(\tilde {U}^G_\sigma )^*}$
in Theorem 7.6 agrees with the one computed in [Reference Orlik and Solomon16, Section 6].
${(\tilde {U}^G_\sigma )^*}$
in Theorem 7.6 agrees with the one computed in [Reference Orlik and Solomon16, Section 6].
In the following result, we identify the G-module
![]() ${U^N_\sigma }$
when
${U^N_\sigma }$
when
![]() $N=G(ab,db,r)$
as in Theorem 6.1(r.b) for
$N=G(ab,db,r)$
as in Theorem 6.1(r.b) for
![]() $r\geq 2$
.
$r\geq 2$
.
Proposition 7.8. Let
![]() $a=de$
and
$a=de$
and
![]() $N=G(ab,db,r)\trianglelefteq G(ab,b,r)=G$
, and fix
$N=G(ab,db,r)\trianglelefteq G(ab,b,r)=G$
, and fix
![]() $\sigma : \zeta _{ab} \to \zeta _{ab}^s$
for
$\sigma : \zeta _{ab} \to \zeta _{ab}^s$
for
![]() $1 \leq s < ab$
with
$1 \leq s < ab$
with
![]() $\gcd (s,ab)=1$
. Then
$\gcd (s,ab)=1$
. Then
![]() $H\simeq C_d$
and
$H\simeq C_d$
and
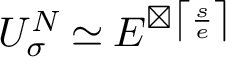 ${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{e}\right \rceil }$
as G-modules.
${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{e}\right \rceil }$
as G-modules.
Proof. Note that for this choice of G and N, with fundamental invariants defined as in Equation (14), we have
![]() ${N}_i={G}_i$
for
${N}_i={G}_i$
for
![]() $i=1,\dots ,r-1$
, and
$i=1,\dots ,r-1$
, and
![]() ${N}_r=(x_1\cdots x_r)^e$
while
${N}_r=(x_1\cdots x_r)^e$
while
![]() ${G}_r=(x_1\cdots x_r)^a$
. The matrix
${G}_r=(x_1\cdots x_r)^a$
. The matrix
![]() $\mathrm {diag}(\zeta _a,1,\dots ,1)\in G$
maps to the cyclic generator
$\mathrm {diag}(\zeta _a,1,\dots ,1)\in G$
maps to the cyclic generator
![]() $c\in C_d\simeq H$
, acting trivially on
$c\in C_d\simeq H$
, acting trivially on
![]() ${\mathrm {span}}_{\mathbb {C}}\{{N}_1,\dots ,{N}_{r-1}\}$
and mapping
${\mathrm {span}}_{\mathbb {C}}\{{N}_1,\dots ,{N}_{r-1}\}$
and mapping
![]() $c:{N}_r\mapsto \zeta _d{N}_r$
, where
$c:{N}_r\mapsto \zeta _d{N}_r$
, where
![]() $\zeta _d:=\zeta _a^{-e}$
is a primitive dth root of unity.
$\zeta _d:=\zeta _a^{-e}$
is a primitive dth root of unity.
On the other hand, we see that the space
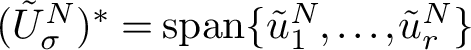 $(\tilde{U}^N_\sigma)^* ={\mathrm {span}}\{\tilde {u}_1^N,\dots ,\tilde {u}_r^N\}$
constructed in Theorem 7.6 is G-stable and the
$(\tilde{U}^N_\sigma)^* ={\mathrm {span}}\{\tilde {u}_1^N,\dots ,\tilde {u}_r^N\}$
constructed in Theorem 7.6 is G-stable and the
![]() $\tilde {u}_i^N$
form a homogeneous basis for
$\tilde {u}_i^N$
form a homogeneous basis for
![]() $(S(V^*)\otimes {(V^\sigma )^*})^N$
as a free
$(S(V^*)\otimes {(V^\sigma )^*})^N$
as a free
![]() $S(V^*)^N$
-module, and therefore it is isomorphic to
$S(V^*)^N$
-module, and therefore it is isomorphic to
![]() ${(U^N_\sigma )^*}$
as a graded G-module by Lemma 3.6. We see that
${(U^N_\sigma )^*}$
as a graded G-module by Lemma 3.6. We see that
![]() $\mathrm {diag}(\zeta _a,1,\dots ,1)\in G$
acts trivially on
$\mathrm {diag}(\zeta _a,1,\dots ,1)\in G$
acts trivially on
![]() ${\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1^N,\dots ,\tilde {u}_{r-1}^N\}$
and maps
${\mathrm {span}}_{\mathbb {C}}\{\tilde {u}_1^N,\dots ,\tilde {u}_{r-1}^N\}$
and maps
 $c:\tilde {u}_r^N\mapsto \zeta _a^{-e\left \lceil \frac {s}{e}\right \rceil }\tilde {u}_r^N=\zeta _d^{\left \lceil \frac {s}{e}\right \rceil }\tilde {u}_r^N$
.
$c:\tilde {u}_r^N\mapsto \zeta _a^{-e\left \lceil \frac {s}{e}\right \rceil }\tilde {u}_r^N=\zeta _d^{\left \lceil \frac {s}{e}\right \rceil }\tilde {u}_r^N$
.
Note that we do not necessarily have that
![]() $\lceil \frac {s}{e}\rceil $
is relatively prime to d. When
$\lceil \frac {s}{e}\rceil $
is relatively prime to d. When
![]() $d=a$
so that
$d=a$
so that
![]() $e=1$
and
$e=1$
and
![]() $N=G(ab,ab,r)$
,
$N=G(ab,ab,r)$
,
![]() $G/N\simeq C_a=\langle c\rangle $
acts by
$G/N\simeq C_a=\langle c\rangle $
acts by
![]() $c: u_r^N \to \zeta _a^{-s} u_r^N,$
so that
$c: u_r^N \to \zeta _a^{-s} u_r^N,$
so that
![]() ${U^N_\sigma } \simeq E^\sigma $
. Another special case occurs when
${U^N_\sigma } \simeq E^\sigma $
. Another special case occurs when
![]() $s<e$
, so that
$s<e$
, so that
![]() ${U^N_\sigma } \simeq E$
.
${U^N_\sigma } \simeq E$
.
In the following result, we identify the representation
![]() ${U^N_\sigma }$
when
${U^N_\sigma }$
when
![]() $G=(2ab,2d,2)$
and
$G=(2ab,2d,2)$
and
![]() $N=G(ab,a,2)$
as in Theorem 6.1(
$N=G(ab,a,2)$
as in Theorem 6.1(
![]() $2$
.c). In this case it is not possible to write
$2$
.c). In this case it is not possible to write
![]() ${U^N_\sigma }$
as a fake tensor power (Definition 7.3) of
${U^N_\sigma }$
as a fake tensor power (Definition 7.3) of
![]() ${E}$
in general.
${E}$
in general.
Proposition 7.9. Let
![]() $a=de$
and
$a=de$
and
![]() $N=G(ab,a,2)\triangleleft G(2ab,2d,2)=G$
, and fix
$N=G(ab,a,2)\triangleleft G(2ab,2d,2)=G$
, and fix
![]() $\sigma :\zeta _{2ab}\mapsto \zeta _{2ab}^s$
for
$\sigma :\zeta _{2ab}\mapsto \zeta _{2ab}^s$
for
![]() $1\leq s<2ab$
with
$1\leq s<2ab$
with
![]() $\mathrm {gcd}(s,2ab)=1$
. Then
$\mathrm {gcd}(s,2ab)=1$
. Then
![]() $H\simeq C_2\times C_e$
and
$H\simeq C_2\times C_e$
and
![]() ${E}\simeq \lambda _2\oplus \lambda _e$
, where
${E}\simeq \lambda _2\oplus \lambda _e$
, where
![]() $\lambda _2$
is the standard reflection representation of
$\lambda _2$
is the standard reflection representation of
![]() $C_2$
and
$C_2$
and
![]() $\lambda _e$
is the standard reflection representation of
$\lambda _e$
is the standard reflection representation of
![]() $C_e$
, and
$C_e$
, and
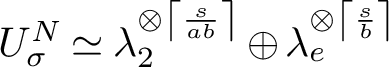 ${U^N_\sigma }\simeq \lambda _2^{\otimes \left \lceil \frac {s}{ab}\right \rceil }\oplus \lambda _e^{\otimes \left \lceil \frac {s}{b}\right \rceil }$
as H-modules.
${U^N_\sigma }\simeq \lambda _2^{\otimes \left \lceil \frac {s}{ab}\right \rceil }\oplus \lambda _e^{\otimes \left \lceil \frac {s}{b}\right \rceil }$
as H-modules.
Proof. We may choose the fundamental N-invariants
as in Equation (14). Letting
 $$\begin{align*}h_1:=\begin{pmatrix}0&\zeta_{2ab}\\\zeta_{2ab}^{-1} & 0\end{pmatrix}\qquad\text{and}\qquad h_2:=\begin{pmatrix}\zeta_{eb}&0\\0&1\end{pmatrix}.\end{align*}$$
$$\begin{align*}h_1:=\begin{pmatrix}0&\zeta_{2ab}\\\zeta_{2ab}^{-1} & 0\end{pmatrix}\qquad\text{and}\qquad h_2:=\begin{pmatrix}\zeta_{eb}&0\\0&1\end{pmatrix}.\end{align*}$$
We see that
![]() $h_i({N}_j)={N}_j$
if
$h_i({N}_j)={N}_j$
if
![]() $i\neq j$
,
$i\neq j$
,
![]() $h_1({N}_1)=-{N}_1$
, and
$h_1({N}_1)=-{N}_1$
, and
 $h_2({N}_2)=\zeta _e{N}_2$
, where
$h_2({N}_2)=\zeta _e{N}_2$
, where
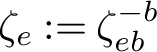 $\zeta_e:=\zeta_{eb}^{-b}$
, and therefore
$\zeta_e:=\zeta_{eb}^{-b}$
, and therefore
![]() $h_1$
and
$h_1$
and
![]() $h_2$
map to the generators of the cyclic factors in the bicyclic quotient group
$h_2$
map to the generators of the cyclic factors in the bicyclic quotient group
![]() $H\simeq C_2\times C_e$
. By Theorem 7.6 and Lemma 3.6
$H\simeq C_2\times C_e$
. By Theorem 7.6 and Lemma 3.6
 $(\tilde {U}^N_\sigma )^*={\mathrm {span}}\{\tilde {u}_1^N,\tilde {u}_2^N\}$
is isomorphic to
$(\tilde {U}^N_\sigma )^*={\mathrm {span}}\{\tilde {u}_1^N,\tilde {u}_2^N\}$
is isomorphic to
![]() ${(U^N_\sigma )^*}$
as a graded G-module, where
${(U^N_\sigma )^*}$
as a graded G-module, where
 $$ \begin{align*}\tilde{u}_1^N&=x_1^{\left\lceil\frac{s}{ab}\right\rceil ab -s}\otimes x_1^\sigma + x_2^{\left\lceil\frac{s}{ab}\right\rceil ab -s}\otimes x_2^\sigma;\qquad \text{and}\\ \tilde{u}_2^N&=(x_1x_2)^{\left\lceil \frac{s}{b}\right\rceil b}x_1^{-s}\otimes x_1^\sigma + (x_1x_2)^{\left\lceil \frac{s}{b}\right\rceil b}x_2^{-s}\otimes x_2^\sigma. \end{align*} $$
$$ \begin{align*}\tilde{u}_1^N&=x_1^{\left\lceil\frac{s}{ab}\right\rceil ab -s}\otimes x_1^\sigma + x_2^{\left\lceil\frac{s}{ab}\right\rceil ab -s}\otimes x_2^\sigma;\qquad \text{and}\\ \tilde{u}_2^N&=(x_1x_2)^{\left\lceil \frac{s}{b}\right\rceil b}x_1^{-s}\otimes x_1^\sigma + (x_1x_2)^{\left\lceil \frac{s}{b}\right\rceil b}x_2^{-s}\otimes x_2^\sigma. \end{align*} $$
We see that
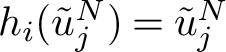 $h_i(\tilde {u}^N_j)=\tilde {u}^N_j$
if
$h_i(\tilde {u}^N_j)=\tilde {u}^N_j$
if
![]() $i\neq j$
,
$i\neq j$
,
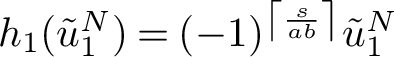 $h_1(\tilde {u}_1^N)=(-1)^{\left \lceil \frac {s}{ab}\right \rceil }\tilde {u}_1^N$
, and
$h_1(\tilde {u}_1^N)=(-1)^{\left \lceil \frac {s}{ab}\right \rceil }\tilde {u}_1^N$
, and
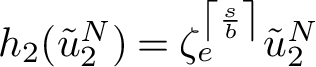 $h_2(\tilde {u}^N_2)=\zeta _e^{\left \lceil \frac {s}{b}\right \rceil }\tilde {u}_2^N$
.
$h_2(\tilde {u}^N_2)=\zeta _e^{\left \lceil \frac {s}{b}\right \rceil }\tilde {u}_2^N$
.
As before, note that we do not necessarily have that
![]() $\left \lceil \frac {s}{b}\right \rceil $
is relatively prime to e. When
$\left \lceil \frac {s}{b}\right \rceil $
is relatively prime to e. When
![]() $b=1$
, we have that
$b=1$
, we have that
![]() ${U^N_\sigma }\simeq {E^\sigma }$
whenever
${U^N_\sigma }\simeq {E^\sigma }$
whenever
![]() $s<a$
. When
$s<a$
. When
![]() $a=1$
we do have
$a=1$
we do have
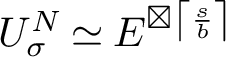 ${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{b}\right \rceil }$
as in the previous cases. Another special case occurs when
${U^N_\sigma }\simeq {E}^{\boxtimes \left \lceil \frac {s}{b}\right \rceil }$
as in the previous cases. Another special case occurs when
![]() $s<b$
, so that
$s<b$
, so that
![]() ${U^N_\sigma }\simeq {E}$
.
${U^N_\sigma }\simeq {E}$
.
7.3 An exceptional example
 $G_{15} \triangleright G_{12}$
$G_{15} \triangleright G_{12}$
To illustrate the choice of indexing of degrees and exponents that is needed in Theorem 1.3, consider
 $$ \begin{align*}G:= G_{15}=\left\langle \left(\begin{array}{cc}1 & 0\\0 & -1\end{array}\right),\frac{\zeta_3}{2}\left(\begin{array}{cc}-1-i & 1-i\\-1-i & -1+i\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & -1\\-1 & -1\end{array}\right) \right\rangle,\end{align*} $$
$$ \begin{align*}G:= G_{15}=\left\langle \left(\begin{array}{cc}1 & 0\\0 & -1\end{array}\right),\frac{\zeta_3}{2}\left(\begin{array}{cc}-1-i & 1-i\\-1-i & -1+i\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & -1\\-1 & -1\end{array}\right) \right\rangle,\end{align*} $$
where we use the conventions in [Reference Lehrer and Taylor14, Chapter 3] and the given matrices describe the action of G on
![]() $V^*$
. We will write the reflection generators of this non-well-generated reflection group G as
$V^*$
. We will write the reflection generators of this non-well-generated reflection group G as
![]() $\mathbf {s}$
,
$\mathbf {s}$
,
![]() $\mathbf {t}$
and
$\mathbf {t}$
and
![]() $\mathbf {u}$
, in the order they appear above. The degrees of G are
$\mathbf {u}$
, in the order they appear above. The degrees of G are
![]() $d_1^G=12$
and
$d_1^G=12$
and
![]() $d_2^G=24$
, with corresponding invariant generators of
$d_2^G=24$
, with corresponding invariant generators of
![]() $S(V^*)^G$
given by
$S(V^*)^G$
given by
We then have the following normal reflection subgroup
![]() $N\trianglelefteq G$
generated by the reflections
$N\trianglelefteq G$
generated by the reflections
![]() $\mathbf {u}$
,
$\mathbf {u}$
,
![]() $\mathbf {sus}^{-1}$
and
$\mathbf {sus}^{-1}$
and
![]() $\mathbf {tsus}^{-1}\mathbf {t}^{-1}$
:
$\mathbf {tsus}^{-1}\mathbf {t}^{-1}$
:
 $$ \begin{align*}N:= G_{12}=\left\langle\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & -1\\-1 & -1\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & 1\\1 & -1\end{array}\right),\left(\begin{array}{cc}0 & \zeta_8\\\zeta_8^{-1} & 0\end{array}\right) \right\rangle,\end{align*} $$
$$ \begin{align*}N:= G_{12}=\left\langle\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & -1\\-1 & -1\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1 & 1\\1 & -1\end{array}\right),\left(\begin{array}{cc}0 & \zeta_8\\\zeta_8^{-1} & 0\end{array}\right) \right\rangle,\end{align*} $$
where again the above matrices describe the acion of N on its dual reflection representation
![]() $V^{*}$
. The degrees of N are
$V^{*}$
. The degrees of N are
![]() $d_1^N=6$
and
$d_1^N=6$
and
![]() $d_2^N=8$
, with corresponding invariant generators of
$d_2^N=8$
, with corresponding invariant generators of
![]() $S(V^*)^N$
given by
$S(V^*)^N$
given by
Then the quotient group
![]() $H:=G/N\simeq C_2 \times C_3$
, and by Theorem 1.2 H acts in a reflection representation on
$H:=G/N\simeq C_2 \times C_3$
, and by Theorem 1.2 H acts in a reflection representation on
![]() ${E}$
, where
${E}$
, where
![]() ${E^*}={\mathrm {span}}_{\mathbb {C}}\{N_1,N_2\}$
, because
${E^*}={\mathrm {span}}_{\mathbb {C}}\{N_1,N_2\}$
, because
 $$ \begin{align*} \mathbf{s}(N_1)&=-N_1, \qquad \mathbf{s}(N_2)=N_2\\ \mathbf{t}(N_1)&=N_1,\qquad \mathbf{t}(N_2)=\zeta_3^2 N_2\\ \mathbf{u}(N_1)&=N_1, \qquad \mathbf{u}(N_2)=N_2. \end{align*} $$
$$ \begin{align*} \mathbf{s}(N_1)&=-N_1, \qquad \mathbf{s}(N_2)=N_2\\ \mathbf{t}(N_1)&=N_1,\qquad \mathbf{t}(N_2)=\zeta_3^2 N_2\\ \mathbf{u}(N_1)&=N_1, \qquad \mathbf{u}(N_2)=N_2. \end{align*} $$
Compatible with the choices of invariant generators
![]() ${G}_1$
and
${G}_1$
and
![]() ${G}_2$
for G and
${G}_2$
for G and
![]() ${N}_1$
and
${N}_1$
and
![]() ${N}_2$
for N, we find invariant generators of
${N}_2$
for N, we find invariant generators of
![]() $S({E^*})^H$
that are
$S({E^*})^H$
that are
![]() $\mathbf {N}$
-homogeneous of degrees
$\mathbf {N}$
-homogeneous of degrees
![]() $d_1^H=2$
and
$d_1^H=2$
and
![]() $d_2^H=3$
:
$d_2^H=3$
:
and also
![]() $\mathbf {x}$
-homogeneous of degrees
$\mathbf {x}$
-homogeneous of degrees
![]() $d_1^G=12=d_1^N\cdot d_1^H$
and
$d_1^G=12=d_1^N\cdot d_1^H$
and
![]() $d_2^G=24=d_2^N\cdot d_2^H$
.
$d_2^G=24=d_2^N\cdot d_2^H$
.
As we can see from the explicit matrices above, the reflection representation of G is actually defined over
![]() $\zeta _{24}$
. For s coprime to
$\zeta _{24}$
. For s coprime to
![]() $24$
we write
$24$
we write
![]() $\sigma _s$
for the Galois automorphism
$\sigma _s$
for the Galois automorphism
![]() $\sigma _s\in \mathrm {Gal}(\mathbb {Q}(\zeta _{24})/\mathbb {Q})$
defined by
$\sigma _s\in \mathrm {Gal}(\mathbb {Q}(\zeta _{24})/\mathbb {Q})$
defined by
![]() $\sigma _s:\zeta _{24}\mapsto \zeta _{24}^s$
. The complete data for every Galois twist
$\sigma _s:\zeta _{24}\mapsto \zeta _{24}^s$
. The complete data for every Galois twist
![]() ${V^\sigma }$
for
${V^\sigma }$
for
![]() $G=G_{15}$
and
$G=G_{15}$
and
![]() $N=G_{12}$
appear in Table 2. Code for computing similar examples using Sage can be found at [Reference Arreche and Williams2].
$N=G_{12}$
appear in Table 2. Code for computing similar examples using Sage can be found at [Reference Arreche and Williams2].
Table 2 Data for
![]() $G=G_{15}$
,
$G=G_{15}$
,
![]() $N=G_{12}$
and
$N=G_{12}$
and
![]() $H=G/N=C_2\times C_3$
computed using [Reference Arreche and Williams2]. The rows are indexed by the Galois twists
$H=G/N=C_2\times C_3$
computed using [Reference Arreche and Williams2]. The rows are indexed by the Galois twists
![]() $\sigma _s:\zeta _{24}\to \zeta _{24}^s$
(for s coprime to
$\sigma _s:\zeta _{24}\to \zeta _{24}^s$
(for s coprime to
![]() $24$
). The columns contain the degrees of N multiplied by the
$24$
). The columns contain the degrees of N multiplied by the
![]() ${E^\sigma }$
-exponents of H to obtain the
${E^\sigma }$
-exponents of H to obtain the
![]() ${E^\sigma }$
-exponents of G and the
${E^\sigma }$
-exponents of G and the
![]() ${V^\sigma }$
-exponents of N added to the
${V^\sigma }$
-exponents of N added to the
![]() ${U^N_\sigma }$
-exponents of G to obtain the
${U^N_\sigma }$
-exponents of G to obtain the
![]() ${V^\sigma }$
-exponents of G, indexed according to Theorem 1.3. The final column lists the corresponding product sides of the weighted sums over G according to Theorem 1.4.
${V^\sigma }$
-exponents of G, indexed according to Theorem 1.3. The final column lists the corresponding product sides of the weighted sums over G according to Theorem 1.4.

Let us work out the case
![]() $\sigma =\sigma _{13}$
in detail; the other cases are similar. Writing
$\sigma =\sigma _{13}$
in detail; the other cases are similar. Writing
![]() $x^\sigma $
and
$x^\sigma $
and
![]() $y^\sigma $
for the basis vectors of
$y^\sigma $
for the basis vectors of
![]() ${(V^\sigma )^*}$
as before, we find bases
${(V^\sigma )^*}$
as before, we find bases
![]() $\{u_1^G,u_2^G\}$
for
$\{u_1^G,u_2^G\}$
for
![]() ${(U^G_\sigma )^*}$
and
${(U^G_\sigma )^*}$
and
![]() $\{u_1^N,u_2^N\}$
for
$\{u_1^N,u_2^N\}$
for
![]() ${(U^N_\sigma )^*}$
given by
${(U^N_\sigma )^*}$
given by
 $$ \begin{align*} u_1^G&=(x^{11} - 22 x^7 y^4 - 11 x^3 y^8) \otimes x^\sigma \\ &+(y^{11} - 22 x^4 y^7 - 11 x^8 y^3) \otimes y^\sigma ;\\ u_2^G&=\left((x^{21}y^2- xy^{22}) + 27(x^{17}y^6-x^5y^{18}) + 170(x^{13}y^{10} - x^9 y^{14}) \right)\otimes x^\sigma \\ &+\left((x^2y^{21}- x^{22}y) + 27(x^6y^{17}- x^{18}y^5) +170(x^{10}y^{13}- x^{14}y^9)\right)\otimes y^\sigma;\\ u_1^N&=u_1^G; \text{ and }\\ u_2^N&=y\otimes x^\sigma - x\otimes y^\sigma. \end{align*} $$
$$ \begin{align*} u_1^G&=(x^{11} - 22 x^7 y^4 - 11 x^3 y^8) \otimes x^\sigma \\ &+(y^{11} - 22 x^4 y^7 - 11 x^8 y^3) \otimes y^\sigma ;\\ u_2^G&=\left((x^{21}y^2- xy^{22}) + 27(x^{17}y^6-x^5y^{18}) + 170(x^{13}y^{10} - x^9 y^{14}) \right)\otimes x^\sigma \\ &+\left((x^2y^{21}- x^{22}y) + 27(x^6y^{17}- x^{18}y^5) +170(x^{10}y^{13}- x^{14}y^9)\right)\otimes y^\sigma;\\ u_1^N&=u_1^G; \text{ and }\\ u_2^N&=y\otimes x^\sigma - x\otimes y^\sigma. \end{align*} $$
Writing
![]() $u_i^G=a_{i1}^G\otimes x^\sigma +a_{i2}^G\otimes y^\sigma $
and
$u_i^G=a_{i1}^G\otimes x^\sigma +a_{i2}^G\otimes y^\sigma $
and
![]() $u_i^N=a_{i1}^N\otimes x^\sigma +a_{i2}^N\otimes y_\sigma $
as above, let us verify that
$u_i^N=a_{i1}^N\otimes x^\sigma +a_{i2}^N\otimes y_\sigma $
as above, let us verify that
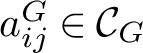 $a_{ij}^G\in {\mathcal {C}_G}$
and
$a_{ij}^G\in {\mathcal {C}_G}$
and
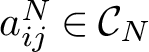 $a_{ij}^N\in {\mathcal {C}_N}$
. It is clear that
$a_{ij}^N\in {\mathcal {C}_N}$
. It is clear that
![]() $a_{11}^G,a_{12}^G\in {\mathcal {C}_G}$
, because
$a_{11}^G,a_{12}^G\in {\mathcal {C}_G}$
, because
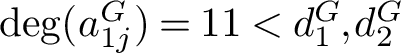 $\mathrm {deg}(a_{1j}^G)=11<d_1^G,d_2^G$
, and every polynomial of degree smaller than every degree of G belongs to
$\mathrm {deg}(a_{1j}^G)=11<d_1^G,d_2^G$
, and every polynomial of degree smaller than every degree of G belongs to
![]() ${\mathcal {C}_G}$
. Similarly, we see that
${\mathcal {C}_G}$
. Similarly, we see that
![]() $a_{21}^N,a_{22}^N\in {\mathcal {C}_N}$
, because
$a_{21}^N,a_{22}^N\in {\mathcal {C}_N}$
, because
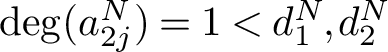 $\mathrm {deg}(a_{2j}^N)=1<d_1^N,d_2^N$
. We observe that
$\mathrm {deg}(a_{2j}^N)=1<d_1^N,d_2^N$
. We observe that
![]() $u_2^G={N}_1{N}_2^2\cdot u_2^N$
(we discuss the meaning of this observation in more detail below), and therefore
$u_2^G={N}_1{N}_2^2\cdot u_2^N$
(we discuss the meaning of this observation in more detail below), and therefore
![]() $u_2^G\in {\mathcal {C}_G}\otimes {(V^\sigma )^*}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}\otimes {(V^\sigma )^*}$
by Proposition 3.3. To see that
$u_2^G\in {\mathcal {C}_G}\otimes {(V^\sigma )^*}\simeq {\mathcal {C}_H}\otimes {\mathcal {C}_N}\otimes {(V^\sigma )^*}$
by Proposition 3.3. To see that
![]() $u_1^N\in {\mathcal {C}_N}\otimes {(V^\sigma )^*}$
also, suppose that
$u_1^N\in {\mathcal {C}_N}\otimes {(V^\sigma )^*}$
also, suppose that
![]() $w_1^N,u_2^N$
is a homogeneous basis for
$w_1^N,u_2^N$
is a homogeneous basis for
![]() ${(U^N_\sigma )^*}$
, and let
${(U^N_\sigma )^*}$
, and let
![]() $p_1,p_2\in S(V^*)^N$
be homogeneous such that
$p_1,p_2\in S(V^*)^N$
be homogeneous such that
![]() $u_1^N=p_1w_1^N+p_2u_2^N$
. But then
$u_1^N=p_1w_1^N+p_2u_2^N$
. But then
![]() $p_2=0$
, because no homogeneous N-invariant polynomial has degree
$p_2=0$
, because no homogeneous N-invariant polynomial has degree
![]() $10$
, which implies that
$10$
, which implies that
 $a_{1j}^N$
is divisible by a homogeneous N-invariant polynomial
$a_{1j}^N$
is divisible by a homogeneous N-invariant polynomial
![]() $p_1$
with
$p_1$
with
![]() $\mathrm {deg}(p_1)\leq 11$
. But the only nonconstant choices are
$\mathrm {deg}(p_1)\leq 11$
. But the only nonconstant choices are
![]() $p_1\,{=}\,{N}_1$
or
$p_1\,{=}\,{N}_1$
or
![]() $p_1={N}_2$
, none of which divide the coefficients
$p_1={N}_2$
, none of which divide the coefficients
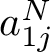 $a_{1j}^N$
above, and therefore
$a_{1j}^N$
above, and therefore
![]() $p_1\in \mathbb {C}^\times $
. This concludes the proof that the
$p_1\in \mathbb {C}^\times $
. This concludes the proof that the
![]() $u_i^G$
and
$u_i^G$
and
![]() $u_i^N$
specified above are indeed bases for
$u_i^N$
specified above are indeed bases for
![]() ${(U^G_\sigma )^*}$
and
${(U^G_\sigma )^*}$
and
![]() ${(U^N_\sigma )^*}$
, respectively, as claimed.
${(U^N_\sigma )^*}$
, respectively, as claimed.
Hence, the
![]() ${V^\sigma }$
-exponents of G are
${V^\sigma }$
-exponents of G are
![]() $e_1^G(V^\sigma )=11$
and
$e_1^G(V^\sigma )=11$
and
![]() $e_2^G(V^\sigma )=23$
, and the
$e_2^G(V^\sigma )=23$
, and the
![]() ${V^\sigma }$
-exponents of N are
${V^\sigma }$
-exponents of N are
![]() $e_1^N(V^\sigma )=11$
and
$e_1^N(V^\sigma )=11$
and
![]() $e_2^N(V^\sigma )=1$
. We compute the action of G on
$e_2^N(V^\sigma )=1$
. We compute the action of G on
![]() ${(U^N_\sigma )^*}$
and obtain
${(U^N_\sigma )^*}$
and obtain
 $$ \begin{align*} g(u_1^N)&=u_1^N \text{ for all } g \in G,\\ \mathbf{s}(u_2^N)&=-u_2^N, \\ \mathbf{t}(u_2^N)&=\zeta_3^2 u_2^N \text{ and }\\ \mathbf{u}(u_2^N)&=u_2^N. \end{align*} $$
$$ \begin{align*} g(u_1^N)&=u_1^N \text{ for all } g \in G,\\ \mathbf{s}(u_2^N)&=-u_2^N, \\ \mathbf{t}(u_2^N)&=\zeta_3^2 u_2^N \text{ and }\\ \mathbf{u}(u_2^N)&=u_2^N. \end{align*} $$
The resulting G-module structure on
![]() ${U^N_\sigma }$
yields the direct sum of the trivial representation with the unique 1-dimensional representation of G with fake degree
${U^N_\sigma }$
yields the direct sum of the trivial representation with the unique 1-dimensional representation of G with fake degree
![]() $q^{22}$
, which is G-isomorphic to the
$q^{22}$
, which is G-isomorphic to the
![]() $\mathbb {C}$
-span of the G-harmonic semi-invariant homogeneous polynomial
$\mathbb {C}$
-span of the G-harmonic semi-invariant homogeneous polynomial
so that a basis for
![]() $({\mathcal {C}_G}\otimes {(U^N_\sigma )^*})^G$
is given by
$({\mathcal {C}_G}\otimes {(U^N_\sigma )^*})^G$
is given by
![]() $\{1\otimes u_1^N,a_{22}^H\otimes u_2^N\}$
.
$\{1\otimes u_1^N,a_{22}^H\otimes u_2^N\}$
.
On the other hand, the H-module structure on
![]() ${U^N_\sigma }$
yields the direct sum of the trivial representation with the
${U^N_\sigma }$
yields the direct sum of the trivial representation with the
![]() $1$
-dimensional representation of H with fake degree
$1$
-dimensional representation of H with fake degree
![]() $q^3$
given by the
$q^3$
given by the
![]() $\mathbb {C}$
-span of the H-harmonic semi-invariant
$\mathbb {C}$
-span of the H-harmonic semi-invariant
![]() $\mathbf {N}$
-homogeneous polynomial
$\mathbf {N}$
-homogeneous polynomial
so that a basis for
![]() $({\mathcal {C}_H}\otimes {(U^N_\sigma )^*})^H$
is given by
$({\mathcal {C}_H}\otimes {(U^N_\sigma )^*})^H$
is given by
![]() $\{1\otimes u_1^N,{N}_1{N}_2^2\otimes u_2^N\}$
.
$\{1\otimes u_1^N,{N}_1{N}_2^2\otimes u_2^N\}$
.
Thus, we witness the general isomorphism
from the proof of Corollary 3.7 in this example, because we obtain
![]() $a_{22}^H\otimes u_2^N\mapsto u_2^G$
by collapsing the first tensor in
$a_{22}^H\otimes u_2^N\mapsto u_2^G$
by collapsing the first tensor in
 $$ \begin{align*} a_{22}^H\otimes u_2^N&=(x^5y-xy^5)(x^8+14x^4y^4+y^8)^2\otimes(y\otimes x^\sigma-x\otimes y^\sigma)\in({\mathcal{C}_H}\otimes{(U^N_\sigma)^*})^H\\ &\mapsto (x^5y-xy^5)(x^8+14x^4y^4+y^8)^2(y\otimes x^\sigma-x\otimes y^\sigma)=u_2^G\in({\mathcal{C}_G}\otimes{(V^\sigma)^*})^G. \end{align*} $$
$$ \begin{align*} a_{22}^H\otimes u_2^N&=(x^5y-xy^5)(x^8+14x^4y^4+y^8)^2\otimes(y\otimes x^\sigma-x\otimes y^\sigma)\in({\mathcal{C}_H}\otimes{(U^N_\sigma)^*})^H\\ &\mapsto (x^5y-xy^5)(x^8+14x^4y^4+y^8)^2(y\otimes x^\sigma-x\otimes y^\sigma)=u_2^G\in({\mathcal{C}_G}\otimes{(V^\sigma)^*})^G. \end{align*} $$
Acknowledgements
We thank Theo Douvropoulos for many helpful remarks and suggestions. C. Arreche was partially supported by NSF grant CCF-1815108. N. Williams was partially supported by Simons Foundation award number 585380.