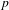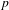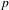Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Molina, Santiago
2019.
Anticyclotomic 𝑝-adic 𝐿-functions and the exceptional zero phenomenon.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 4,
p.
2659.
Disegni, Daniel
2020.
On the p-adic Birch and Swinnerton-Dyer conjecture for elliptic curves over number fields.
Kyoto Journal of Mathematics,
Vol. 60,
Issue. 2,
Castella, Francesc
2020.
ON THE -ADIC VARIATION OF HEEGNER POINTS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 6,
p.
2127.
Bertolini, Massimo
Darmon, Henri
and
Venerucci, Rodolfo
2022.
Heegner points and Beilinson–Kato elements: A conjecture of Perrin-Riou.
Advances in Mathematics,
Vol. 398,
Issue. ,
p.
108172.