Article contents
ON THE NUMBER OF DEDEKIND CUTS AND TWO-CARDINAL MODELS OF DEPENDENT THEORIES
Published online by Cambridge University Press: 23 January 2015
Abstract
For an infinite cardinal  ${\it\kappa}$ , let
${\it\kappa}$ , let 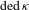 $\text{ded}\,{\it\kappa}$ denote the supremum of the number of Dedekind cuts in linear orders of size
$\text{ded}\,{\it\kappa}$ denote the supremum of the number of Dedekind cuts in linear orders of size  ${\it\kappa}$ . It is known that
${\it\kappa}$ . It is known that 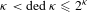 ${\it\kappa}<\text{ded}\,{\it\kappa}\leqslant 2^{{\it\kappa}}$ for all
${\it\kappa}<\text{ded}\,{\it\kappa}\leqslant 2^{{\it\kappa}}$ for all  ${\it\kappa}$ and that
${\it\kappa}$ and that 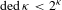 $\text{ded}\,{\it\kappa}<2^{{\it\kappa}}$ is consistent for any
$\text{ded}\,{\it\kappa}<2^{{\it\kappa}}$ is consistent for any  ${\it\kappa}$ of uncountable cofinality. We prove however that
${\it\kappa}$ of uncountable cofinality. We prove however that 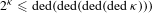 $2^{{\it\kappa}}\leqslant \text{ded}(\text{ded}(\text{ded}(\text{ded}\,{\it\kappa})))$ always holds. Using this result we calculate the Hanf numbers for the existence of two-cardinal models with arbitrarily large gaps and for the existence of arbitrarily large models omitting a type in the class of countable dependent first-order theories. Specifically, we show that these bounds are as large as in the class of all countable theories.
$2^{{\it\kappa}}\leqslant \text{ded}(\text{ded}(\text{ded}(\text{ded}\,{\it\kappa})))$ always holds. Using this result we calculate the Hanf numbers for the existence of two-cardinal models with arbitrarily large gaps and for the existence of arbitrarily large models omitting a type in the class of countable dependent first-order theories. Specifically, we show that these bounds are as large as in the class of all countable theories.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 771 - 784
- Copyright
- © Cambridge University Press 2015
References
- 3
- Cited by

