Article contents
PINNING ON A DEFECT LINE: CHARACTERIZATION OF MARGINAL DISORDER RELEVANCE AND SHARP ASYMPTOTICS FOR THE CRITICAL POINT SHIFT
Published online by Cambridge University Press: 29 January 2016
Abstract
The effect of disorder for pinning models is a subject which has attracted much attention in theoretical physics and rigorous mathematical physics. A peculiar point of interest is the question of coincidence of the quenched and annealed critical point for a small amount of disorder. The question has been mathematically settled in most cases in the last few years, giving in particular a rigorous validation of the Harris criterion on disorder relevance. However, the marginal case, where the return probability exponent is equal to 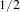 $1/2$ , that is, where the interarrival law of the renewal process is given by
$1/2$ , that is, where the interarrival law of the renewal process is given by 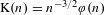 $\text{K}(n)=n^{-3/2}\unicode[STIX]{x1D719}(n)$ where
$\text{K}(n)=n^{-3/2}\unicode[STIX]{x1D719}(n)$ where  $\unicode[STIX]{x1D719}$ is a slowly varying function, has been left partially open. In this paper, we give a complete answer to the question by proving a simple necessary and sufficient criterion on the return probability for disorder relevance, which confirms earlier predictions from the literature. Moreover, we also provide sharp asymptotics on the critical point shift: in the case of the pinning of a one-dimensional simple random walk, the shift of the critical point satisfies the following high temperature asymptotics
$\unicode[STIX]{x1D719}$ is a slowly varying function, has been left partially open. In this paper, we give a complete answer to the question by proving a simple necessary and sufficient criterion on the return probability for disorder relevance, which confirms earlier predictions from the literature. Moreover, we also provide sharp asymptotics on the critical point shift: in the case of the pinning of a one-dimensional simple random walk, the shift of the critical point satisfies the following high temperature asymptotics  $$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0}\unicode[STIX]{x1D6FD}^{2}\log h_{c}(\unicode[STIX]{x1D6FD})=-\frac{\unicode[STIX]{x1D70B}}{2}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0}\unicode[STIX]{x1D6FD}^{2}\log h_{c}(\unicode[STIX]{x1D6FD})=-\frac{\unicode[STIX]{x1D70B}}{2}.\end{eqnarray}$$
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 305 - 346
- Copyright
- © Cambridge University Press 2016
References
- 24
- Cited by

