Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-04T12:44:37.890Z Has data issue: false hasContentIssue false
  • English
  • Français

THE $q$-SCHUR ALGEBRAS AND $q$-SCHUR DUALITIES OF FINITE TYPE

Part of: Linear algebraic groups and related topics Lie algebras and Lie superalgebras Representation theory of groups

Published online by Cambridge University Press:  19 February 2020

Li Luo Open the ORCID record for Li Luo [Opens in a new window]  and
Weiqiang Wang
Li Luo
Affiliation:
School of Mathematical Sciences, Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, Shanghai200241, China (lluo@math.ecnu.edu.cn)
Weiqiang Wang
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22904, USA (ww9c@virginia.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate a $q$-Schur algebra associated with an arbitrary 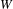$W$-invariant finite set 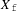$X_{\text{f}}$ of integral weights for a complex simple Lie algebra with Weyl group 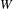$W$. We establish a $q$-Schur duality between the $q$-Schur algebra and Hecke algebra associated with 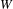$W$. We then realize geometrically the $q$-Schur algebra and duality and construct a canonical basis for the $q$-Schur algebra with positivity. With suitable choices of 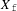$X_{\text{f}}$ in classical types, we recover the $q$-Schur algebras in the literature. Our $q$-Schur algebras are closely related to the category 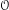${\mathcal{O}}$, where the type 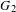$G_{2}$ is studied in detail.

Keywords

Hecke algebrasq-Schur algebrascanonical basis

MSC classification

Primary: 20G43: Schur and $q$-Schur algebras
Secondary: 17B10: Representations, algebraic theory (weights) 20C08: Hecke algebras and their representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 1 , January 2022 , pp. 129 - 160
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bao, H., Kazhdan–Lusztig theory of super type D and quantum symmetric pairs, Represent. Theory 21 (2017), 247–276.CrossRefGoogle Scholar
Bao, H., Kujawa, J., Li, Y. and Wang, W., Geometric Schur duality of classical type, (Appendix by Bao, Li and Wang), Transform. Groups 23 (2018), 329–389.CrossRefGoogle Scholar
Bao, H. and Wang, W., A new approach to Kazhdan–Lusztig theory of type B via quantum symmetric pairs, Astérisque 402 (2018), vii+134 pp.Google Scholar
Bao, H., Wang, W. and Watanabe, H., Multiparameter quantum Schur duality of type B, Proc. Amer. Math. Soc. 146 (2018), 3203–3216.CrossRefGoogle Scholar
Beilinson, A., Lusztig, G. and MacPherson, R., A geometric setting for the quantum deformation of GL n , Duke Math. J. 61 (1990), 655–677.CrossRefGoogle Scholar
Brundan, J., Kazhdan–Lusztig polynomials and character formulae for the Lie superalgebra gl(m|n), J. Amer. Math. Soc. 16 (2003), 185–231.Google Scholar
Cheng, S.-J., Lam, N. and Wang, W., Brundan–Kazhdan–Lusztig conjecture for general linear Lie superalgebras, Duke J. Math. 164 (2015), 617–695.CrossRefGoogle Scholar
Curtis, C., On Lusztig’s isomorphism theorem for Hecke algebras, J. Algebra 92 (1985), 348–365.CrossRefGoogle Scholar
Curtis, C. and Reiner, I., Methods of Representation Theory, Volume I and II (Wiley, New York, 1981/1987).Google Scholar
Deng, B., Du, J., Parshall, B. and Wang., J., Finite Dimensional Algebras and Quantum Groups, Mathematical Surveys and Monographs, Volume 150 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Deodhar, V., On some geometric aspects of Bruhat orderings. II. The parabolic analogue of Kazhdan–Lusztig polynomials, J. Algebra 111 (1987), 483–506.CrossRefGoogle Scholar
Dipper, R. and Donkin, S., Quantum GL n , Proc. Lond. Math. Soc. (3) 63 (1991), 165–211.CrossRefGoogle Scholar
Dipper, R. and James, G., The q-Schur algebra, Proc. Lond. Math. Soc. (3) 59 (1989), 23–50.CrossRefGoogle Scholar
Dipper, R., James, G. and Mathas, A., The (Q, q)-Schur algebra, Proc. Lond. Math. Soc. (3) 77 (1998), 327–361.CrossRefGoogle Scholar
Dipper, R., James, G. and Mathas, A., Cyclotomic q-Schur algebras, Math. Z. 229 (1998), 385–416.CrossRefGoogle Scholar
Donkin, S., On Schur algebras and related algebras I, J. Algebra 104 (1986), 310–328.CrossRefGoogle Scholar
Doty, S., Presenting generalized q-Schur algebras, Represent. Theory 7 (2003), 196–213.CrossRefGoogle Scholar
Doty, S. and Li, Y., A geometric construction of generalized q-Schur algebras, in Recent Advances in Representation Theory, Quantum Groups, Algebraic Geometry, and Related Topics, Contemporary Mathematics, Volume 623, pp. 55–62 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Du, J., Kazhdan–Lusztig bases and isomorphism theorems for q-Schur algebras, in Kazhdan–Lusztig Theory and Related Topics (Chicago, IL, 1989), Contemporary Mathematics, Volume 139, pp. 121–140 (American Mathematical Society, Providence, RI, 1992).CrossRefGoogle Scholar
Du, J., IC bases and quantum linear groups, in Algebraic Groups and Their Generalizations: Quantum and Infinite-Dimensional Methods (University Park, PA, 1991), Proceedings of Symposia in Pure Mathematics, Volume 56, (2) pp. 135–148 (AMS, Providence, RI, 1994).CrossRefGoogle Scholar
Du, J. and Scott, L., The q-Schur2 algebra, Trans. Amer. Math. Soc. 352 (2000), 4325–4353.CrossRefGoogle Scholar
Fan, Z., Lai, C., Li, Y., Luo, L. and Wang, W., Affine flag varieties and quantum symmetric pairs, Mem. Amer. Math. Soc. to appear arXiv:1602.04383v2.Google Scholar
Fan, Z. and Li, Y., Geometric Schur duality of classical type, II, Trans. Amer. Math. Soc. Series B 2 (2015), 51–92.CrossRefGoogle Scholar
Green, R. M., Hyperoctahedral Schur algebras, J. Algebra 192 (1997), 418–438.CrossRefGoogle Scholar
Grojnowski, I. and Lusztig, G., On bases of irreducible representations of quantum GL n , in Kazhdan–Lusztig Theory and Related Topics (Chicago, IL, 1989), Contemporary Mathematics, Volume 139, pp. 167–174 (American Mathematical Society, Providence, RI, 1992).CrossRefGoogle Scholar
Jimbo, M., A q-analogue of U (gl(N + 1)), Hecke algebra, and the Yang–Baxter equation, Lett. Math. Phys. 11 (1986), 247–252.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184.CrossRefGoogle Scholar
Li, Y., A geometric realization of quantum groups of type D, Adv. Math. 224 (2010), 1071–1096.CrossRefGoogle Scholar
Lusztig, G., Introduction to Quantum Groups, Progress in Mathematics, Volume 10 (Birkhäuser Boston, Inc., Boston, MA, 1993).Google Scholar