Article contents
RANK TWO TOPOLOGICAL AND INFINITESIMAL EMBEDDED JUMP LOCI OF QUASI-PROJECTIVE MANIFOLDS
Published online by Cambridge University Press: 15 February 2018
Abstract
We study the germs at the origin of 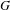 $G$-representation varieties and the degree 1 cohomology jump loci of fundamental groups of quasi-projective manifolds. Using the Morgan–Dupont model associated to a convenient compactification of such a manifold, we relate these germs to those of their infinitesimal counterparts, defined in terms of flat connections on those models. When the linear algebraic group
$G$-representation varieties and the degree 1 cohomology jump loci of fundamental groups of quasi-projective manifolds. Using the Morgan–Dupont model associated to a convenient compactification of such a manifold, we relate these germs to those of their infinitesimal counterparts, defined in terms of flat connections on those models. When the linear algebraic group 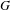 $G$ is either
$G$ is either 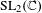 $\text{SL}_{2}(\mathbb{C})$ or its standard Borel subgroup and the depth of the jump locus is 1, this dictionary works perfectly, allowing us to describe in this way explicit irreducible decompositions for the germs of these embedded jump loci. On the other hand, if either
$\text{SL}_{2}(\mathbb{C})$ or its standard Borel subgroup and the depth of the jump locus is 1, this dictionary works perfectly, allowing us to describe in this way explicit irreducible decompositions for the germs of these embedded jump loci. On the other hand, if either 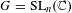 $G=\text{SL}_{n}(\mathbb{C})$ for some
$G=\text{SL}_{n}(\mathbb{C})$ for some 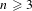 $n\geqslant 3$, or the depth is greater than 1, then certain natural inclusions of germs are strict.
$n\geqslant 3$, or the depth is greater than 1, then certain natural inclusions of germs are strict.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 451 - 485
- Copyright
- © Cambridge University Press 2018
Footnotes
The first author’s work was partially supported by the Romanian Ministry of Research and Innovation, CNCS–UEFISCDI, grant PN-III-P4-ID-PCE-2016-0030, within PNCDI III. The second author was partially supported by the Simons Foundation collaboration grant for mathematicians 354156.
Deceased 10 January 2018.
References
- 1
- Cited by

