1.Benoist, F., Théorie des modèles des corps munis d’une dérivation de Hasse, PhD thesis, Univ. Paris 7 (2005).
2.Benoist, F., A theorem of the Kernel in characteristic 
$p$, preprint, 2011. 4.Benoist, F. and Delon, F. , Questions de corps de définition pour les variétés abéliennes en caractéristique positive, Journal de l’Institut de Mathématiques de Jussieu 7 (2008), 623–639.
5.Bertrand, D., Endomorphismes de groupes algébriques, in Diophantine Approximations and Transcendental Numbers (Luminy, 1982).
6.Bertrand, D. and Pillay, A., A Lindemann–Weierstrass theorem for semiabelian varieties over function fields, J. Amer. Math. Soc. 23 (2010), 491–533.
7.Bouscaren, E. and Delon, F., Groups definable in separably closed fields, Trans. Amer. Math. Soc. 354 (2002), 945–966.
8.Bouscaren, E. and Delon, F., Minimal groups in separably closed fields, J. Symbolic Logic 67 (2002), 239–259.
9.Borel, A., Linear algebraic groups, 2nd enlarged ed., Graduate Text in Mathematics, (Springer, New York, 1991).
10.Buium, A., Differential algebraic group of finite dimension, Lecture Notes in Mathematics 1506 (Springer-Verlag, 1992).
11.Buium, A., Differential Algebra and Diophantine Geometry (Hermann, Paris, 1994).
12.Conrad, B., Chow’s K∕k-image and K∕k-trace and the Lang–Néron theorem, Enseign. Math. (2) 52 (2006), 37–108.
13.Demazure, M. and Gabriel, P., Groupes algébriques Tome I (Masson, Paris, 1970).
14.Erimbetov, M. M., Complete theories with 1-cardinal formulas, Algebra Logika 14 (1975), 245–257.
15.Grothendieck, A. and Raynaud, M., Revêtements étales et groupe fondamental, in Séminaire de géométrie algébrique du Bois Marie (SGA1), 1960–61, Lecture Notes in Mathematics, Volume 224 (Springer-Verlag, 1971).
16.Hrushovski, E., The Mordell–Lang conjecture for function fields, J. Amer. Math. Soc. 9 (1996), 667–690.
17.Kowalski, P. and Pillay, A. , Quantifier elimination for algebraic D-groups, Trans. Amer. Math. Soc. 358 (2006), 167–181.
18.Kowalski, P. and Pillay, A. , On the isotriviality of projective iterative ∂-varieties, J. Pure Appl. Algebra 216 (2012), 20–37.
19.Lang, S., Abelian Varieties (Interscience, London, 1959).
20.Marker, D., Manin kernels, Quaderni Math., Volume 6, pp. 1–21 (Napoli, 2000).
21.Marker, D., Model theory of differential fields, in Model Theory of Fields, second edition, Lecture Notes in Logic (ASL, AK Peters, 2006).
22.Marker, D. and Pillay, A., Differential Galois Theory III: Some inverse problems, Illinois J. Math. 41 (1997), 453–461.
23.Mazur, B. and Messing, W., Universal extensions and one dimensional crystalline cohomology, Lecture Notes in Mathematics, Volume 370 (Springer, 1974).
24.Milne, J. S., Etale cohomology (Princeton University Press, 1980).
25.Moosa, R. and Scanlon, T. , Jet and prolongations spaces, J. Inst. Math. Jussieu 9 (2010), 391–430.
26.Mumford, D., Abelian varieties (Oxford University Press, 1985). Published for the Tata Institute of Fundamental Research, Bombay.
27.Mumford, D. and Fogarty, J., Geometric invariant theory, 2nd enlarged edition (Springer, 1982).
28.Pillay, A., Differential algebraic groups and the number of countable differentially closed fields, in Model Theory of Fields, cited above.
29.Poizat, B., Stable groups, Mathematical Surveys and Monographs (American Mathematical Society, 2001).
30.Rosenlicht, M., Some basic theorems on algebraic groups, Amer. J. Math. 76 (1956), 401–443.
31.Rosenlicht, M., Extensions of vector groups by abelian varieties, Amer. J. Math. 80 (1958), 685–714.
32.Rössler, D., Infinitely p-divisible points on abelian varieties defined over function fields of characteristic p > 0, Notre Dame J. Formal Logic 54 (2013), 579–589.
33.Serre, J.-P., Quelques propriétes des variétes abéliennes en caractéristique p, Amer. J. Math. 80(3) (1958), 715–739.
34.Serre, J.-P., Algebraic groups and class fields, Graduate Texts in Mathematics (Springer, 1988).
35.Shelah, S., Classification Theory, 2nd ed. (North Holland, 1990).
36.Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics (Springer-Verlag, 1986).
37.Vojta, P., Jets via Hasse–Schmidt derivations, in Diophantine Geometry, CRM Series, Volume 4, pp. 335–361 (Ed. Norm., Pisa, 2007).
38.Voloch, F., Diophantine approximation on Abelian varieties in characteristic p, Amer. J. Math. 4 (1995), 1089–1095.
39.Wagner, F. O., Stable groups, London Mathematical Society Lecture Notes (Cambridge University Press, 1997).
41.Ziegler, M., Separably closed field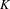s with Hasse derivations, J. Symbolic Logic 68 (2003), 311–318.
$K$
of characteristic 
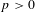$p>0$
and finite degree of imperfection, we study the 
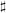$\sharp$
functor which takes a semiabelian variety 
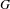$G$
over 
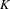$K$
to the maximal divisible subgroup of 
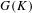$G(K)$
. Our main result is an example where 
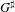$G^{\sharp }$
, as a ‘type-definable group’ in 
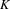$K$
, does not have ‘relative Morley rank’, yielding a counterexample to a claim in Hrushovski [J. Amer. Math. Soc. 9 (1996), 667–690]. Our methods involve studying the question of the preservation of exact sequences by the 
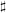$\sharp$
functor, and relating this to issues of descent as well as model-theoretic properties of 
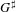$G^{\sharp }$
. We mention some characteristic 0 analogues of these ‘exactness-descent’ results, where differential algebraic methods are more prominent. We also develop the notion of an iterative D-structure on a group scheme over an iterative Hasse field, which is interesting in its own right, as well as providing a uniform treatment of the characteristic 0 and characteristic 
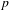$p$
cases of ‘exactness descent’.
