Article contents
SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA
Published online by Cambridge University Press: 25 May 2018
Abstract
This paper sets up the foundations for derived algebraic geometry, Goerss–Hopkins obstruction theory, and the construction of commutative ring spectra in the abstract setting of operadic algebras in symmetric spectra in an (essentially) arbitrary model category. We show that one can do derived algebraic geometry a la Toën–Vezzosi in an abstract category of spectra. We also answer in the affirmative a question of Goerss and Hopkins by showing that the obstruction theory for operadic algebras in spectra can be done in the generality of spectra in an (essentially) arbitrary model category. We construct strictly commutative simplicial ring spectra representing a given cohomology theory and illustrate this with a strictly commutative motivic ring spectrum representing higher order products on Deligne cohomology. These results are obtained by first establishing Smith’s stable positive model structure for abstract spectra and then showing that this category of spectra possesses excellent model-theoretic properties: we show that all colored symmetric operads in symmetric spectra valued in a symmetric monoidal model category are admissible, i.e., algebras over such operads carry a model structure. This generalizes the known model structures on commutative ring spectra and 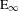 $\text{E}_{\infty }$-ring spectra in simplicial sets or motivic spaces. We also show that any weak equivalence of operads in spectra gives rise to a Quillen equivalence of their categories of algebras. For example, this extends the familiar strictification of
$\text{E}_{\infty }$-ring spectra in simplicial sets or motivic spaces. We also show that any weak equivalence of operads in spectra gives rise to a Quillen equivalence of their categories of algebras. For example, this extends the familiar strictification of 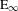 $\text{E}_{\infty }$-rings to commutative rings in a broad class of spectra, including motivic spectra. We finally show that operadic algebras in Quillen equivalent categories of spectra are again Quillen equivalent. This paper is also available at arXiv:1410.5699v2.
$\text{E}_{\infty }$-rings to commutative rings in a broad class of spectra, including motivic spectra. We finally show that operadic algebras in Quillen equivalent categories of spectra are again Quillen equivalent. This paper is also available at arXiv:1410.5699v2.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 707 - 758
- Creative Commons
- This is a work of the U.S. Government and is not subject to copyright protection in the United States.
- Copyright
- © Cambridge University Press 2018
Footnotes
The original version of this article was published with some references containing links to pirated websites. A notice detailing with this has been published and the error rectified in the online PDF and HTML copies.
References
A correction has been issued for this article:
- 9
- Cited by
Linked content
Please note a has been issued for this article.

