Article contents
A VARIANT OF HARISH-CHANDRA FUNCTORS
Published online by Cambridge University Press: 14 August 2017
Abstract
Harish-Chandra induction and restriction functors play a key role in the representation theory of reductive groups over finite fields. In this paper, extending earlier work of Dat, we introduce and study generalisations of these functors which apply to a wide range of finite and profinite groups, typical examples being compact open subgroups of reductive groups over non-archimedean local fields. We prove that these generalisations are compatible with two of the tools commonly used to study the (smooth, complex) representations of such groups, namely Clifford theory and the orbit method. As a test case, we examine in detail the induction and restriction of representations from and to the Siegel Levi subgroup of the symplectic group 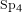 $\text{Sp}_{4}$ over a finite local principal ideal ring of length two. We obtain in this case a Mackey-type formula for the composition of these induction and restriction functors which is a perfect analogue of the well-known formula for the composition of Harish-Chandra functors. In a different direction, we study representations of the Iwahori subgroup
$\text{Sp}_{4}$ over a finite local principal ideal ring of length two. We obtain in this case a Mackey-type formula for the composition of these induction and restriction functors which is a perfect analogue of the well-known formula for the composition of Harish-Chandra functors. In a different direction, we study representations of the Iwahori subgroup 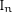 $I_{n}$ of
$I_{n}$ of 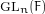 $\text{GL}_{n}(F)$, where
$\text{GL}_{n}(F)$, where 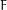 $F$ is a non-archimedean local field. We establish a bijection between the set of irreducible representations of
$F$ is a non-archimedean local field. We establish a bijection between the set of irreducible representations of 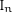 $I_{n}$ and tuples of primitive irreducible representations of smaller Iwahori subgroups, where primitivity is defined by the vanishing of suitable restriction functors.
$I_{n}$ and tuples of primitive irreducible representations of smaller Iwahori subgroups, where primitivity is defined by the vanishing of suitable restriction functors.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 5 , September 2019 , pp. 993 - 1049
- Copyright
- © Cambridge University Press 2017
References
- 5
- Cited by

