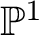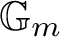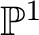1 Introduction
After recalling some preliminaries in §2, this article has two main sections of very different flavors. In §3 we establish a technical result about Rost–Schmid complexes of strictly homotopy-invariant sheaves. Then in §4 we draw applications to the stabilization problem in motivic homotopy theory. We now describe these two main sections in reverse order, and then sketch their relation. For more background and motivation, the reader may wish to consult the introduction of [Reference Bosch, Lütkebohmert and Raynaud2].
1.1
 $\mathbb P^1$
-stabilization in motivic homotopy theory
$\mathbb P^1$
-stabilization in motivic homotopy theory
Motivic homotopy theory is the universal homotopy theory of smooth algebraic varieties, say over a field k. It is built by freely adjoining homotopy colimits to the category of smooth k-varieties, and then enforcing Nisnevich descent and making
![]() $\mathbb A^1$
contractible [Reference Morel and Voevodsky19]. Write
$\mathbb A^1$
contractible [Reference Morel and Voevodsky19]. Write
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
for the pointed version of this theory.Footnote
1
This is a symmetric monoidal category (the monoidal operation being given by the smash product), and every pointed smooth variety defines an object in it. Given a pointed motivic space
$\mathcal {S}\mathrm {pc}{}(k)_*$
for the pointed version of this theory.Footnote
1
This is a symmetric monoidal category (the monoidal operation being given by the smash product), and every pointed smooth variety defines an object in it. Given a pointed motivic space
![]() $\mathcal X \in \mathcal {S}\mathrm {pc}{}(k)_*$
, the classical homotopy groups upgrade to homotopy sheaves
Footnote
2
$\mathcal X \in \mathcal {S}\mathrm {pc}{}(k)_*$
, the classical homotopy groups upgrade to homotopy sheaves
Footnote
2
![]() $\underline {\pi }_i(\mathcal X)$
.
$\underline {\pi }_i(\mathcal X)$
.
The Riemann sphere
 $\mathbb P^1 := \left (\mathbb P^1, 1\right ) \in \mathcal {S}\mathrm {pc}{}(k)_*$
plays a similar role to the ordinary sphere in classical topology. Stable motivic homotopy theory is concerned with the category obtained by making
$\mathbb P^1 := \left (\mathbb P^1, 1\right ) \in \mathcal {S}\mathrm {pc}{}(k)_*$
plays a similar role to the ordinary sphere in classical topology. Stable motivic homotopy theory is concerned with the category obtained by making
![]() $\Sigma _{\mathbb P^1} := \wedge \mathbb P^1$
into an equivalence. It is this context in which algebraic cycles and motivic cohomology naturally appear. We can take a more pedestrian approach. The functor
$\Sigma _{\mathbb P^1} := \wedge \mathbb P^1$
into an equivalence. It is this context in which algebraic cycles and motivic cohomology naturally appear. We can take a more pedestrian approach. The functor
![]() $\Sigma _{\mathbb P^1}$
has a right adjoint
$\Sigma _{\mathbb P^1}$
has a right adjoint
![]() $\Omega _{\mathbb P^1}$
, and there is a directed diagram of endofunctors of
$\Omega _{\mathbb P^1}$
, and there is a directed diagram of endofunctors of
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
:
$\mathcal {S}\mathrm {pc}{}(k)_*$
:
Denote by Q its homotopy colimit. Then
![]() $Q\mathcal X$
is the
$Q\mathcal X$
is the
![]() $\mathbb P^1$
-stabilization of
$\mathbb P^1$
-stabilization of
![]() $\mathcal X$
, and the homotopy sheaves of
$\mathcal X$
, and the homotopy sheaves of
![]() $Q\mathcal X$
are called the
$Q\mathcal X$
are called the
![]() $\mathbb P^1$
-stable homotopy sheaves of
$\mathbb P^1$
-stable homotopy sheaves of
![]() $\mathcal X$
.
$\mathcal X$
.
A simple form of our main application of our technical result is as follows. It is reminiscent of the fact that for an ordinary space X, the sequence of sets
 $\left \{\pi _0 \Omega ^i \Sigma ^i X\right \}_{i \ge 0}$
is given by
$\left \{\pi _0 \Omega ^i \Sigma ^i X\right \}_{i \ge 0}$
is given by
![]() $\pi _0 X$
,
$\pi _0 X$
,
![]() $F \pi _0 X$
,
$F \pi _0 X$
,
![]() $\mathbb {Z}(\pi _0 X)$
,
$\mathbb {Z}(\pi _0 X)$
,
![]() $\mathbb {Z}(\pi _0 X)$
, …, where for a pointed set A,
$\mathbb {Z}(\pi _0 X)$
, …, where for a pointed set A,
![]() $FA$
denotes the free group on A (with identity given by the base point) and
$FA$
denotes the free group on A (with identity given by the base point) and
![]() $\mathbb {Z}(A)$
denotes the free abelian group on A (with
$\mathbb {Z}(A)$
denotes the free abelian group on A (with
![]() $0$
given by the base point).
$0$
given by the base point).
Theorem 1.1. Let k be a perfect field and
![]() $n \ge 3$
(if
$n \ge 3$
(if
![]() $char(k) = 0$
,
$char(k) = 0$
,
![]() $n=2$
is also allowed). Then for
$n=2$
is also allowed). Then for
![]() $\mathcal X \in \mathcal {S}\mathrm {pc}{}(k)_*$
, the canonical map
$\mathcal X \in \mathcal {S}\mathrm {pc}{}(k)_*$
, the canonical map
is an isomorphism.
Proof. This is an immediate consequence of Corollary 4.9 and, for example, Morel’s Hurewicz theorem [18, Theorem 6.37].
Example 1.2. Morel’s computations [18, Corollary 6.43] imply that for
![]() $\mathcal X = S^0$
, already
$\mathcal X = S^0$
, already
![]() $\underline {\pi }_0 Q_2 S^0 \simeq \underline {GW} \simeq \underline {\pi }_0 Q S^0$
. Our result shows that this stabilization is not special to
$\underline {\pi }_0 Q_2 S^0 \simeq \underline {GW} \simeq \underline {\pi }_0 Q S^0$
. Our result shows that this stabilization is not special to
![]() $S^0$
, except that our results are not strong enough to establish stabilization at
$S^0$
, except that our results are not strong enough to establish stabilization at
![]() $Q_2$
, only at
$Q_2$
, only at
![]() $Q_3$
. See also Remark 4.3.
$Q_3$
. See also Remark 4.3.
We also obtain some conservativity results; here is a simple form. It is similar to the fact that stabilization is conservative on simply connected topological spaces. Write
![]() $\mathcal {S}\mathrm {pc}{}(k)_*(n) \subset \mathcal {S}\mathrm {pc}{}(k)_*$
for the subcategory generated under homotopy colimits by objects of the form
$\mathcal {S}\mathrm {pc}{}(k)_*(n) \subset \mathcal {S}\mathrm {pc}{}(k)_*$
for the subcategory generated under homotopy colimits by objects of the form
![]() $X_+ \wedge {\mathbb {G}_m^{\wedge n}}$
, with
$X_+ \wedge {\mathbb {G}_m^{\wedge n}}$
, with
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
(and
$X \in {\mathrm {S}\mathrm {m}}_k$
(and
 ${\mathbb {G}_m} := \left (\mathbb A^1 \setminus 0, 1\right )$
,
${\mathbb {G}_m} := \left (\mathbb A^1 \setminus 0, 1\right )$
,
![]() $X_+ := X \coprod *$
). Denote by
$X_+ := X \coprod *$
). Denote by
![]() $\mathcal {S}\mathrm {pc}{}(k)_{*,\ge 1} \subset \mathcal {S}\mathrm {pc}{}(k)_*$
the subcategory of
$\mathcal {S}\mathrm {pc}{}(k)_{*,\ge 1} \subset \mathcal {S}\mathrm {pc}{}(k)_*$
the subcategory of
![]() $\mathbb A^1$
-simply connected spaces.
$\mathbb A^1$
-simply connected spaces.
Theorem 1.3. Let k be perfect, and put
![]() $n=1$
if
$n=1$
if
![]() $char(k) = 0$
and
$char(k) = 0$
and
![]() $n = 3$
if
$n = 3$
if
![]() $char(k)> 0$
. Then the stabilization functor
$char(k)> 0$
. Then the stabilization functor
is conservative (i.e., detects equivalences).
In particular,
![]() $\Sigma _{\mathbb P^1}$
and all of its iterates, and also
$\Sigma _{\mathbb P^1}$
and all of its iterates, and also
![]() $\Sigma _{\mathbb P^1}^\infty $
, are conservative on the same subcategory.
$\Sigma _{\mathbb P^1}^\infty $
, are conservative on the same subcategory.
Proof. This is an immediate consequence of Corollary 4.15 and, for example, [24, Corollary 2.23].
The results in §4 are stronger than this sample; in fact, they are stated in terms of the stabilization functor from
![]() $S^1$
-spectra to
$S^1$
-spectra to
![]() $\mathbb P^1$
-spectra. The reader is encouraged to skip to this section directly. Our main results in the form of Corollary 4.9, Theorem 4.14, and Corollary 4.15 can be understood without reading the rest of the article (except perhaps for taking a glance at §4.1, where some notation is introduced).
$\mathbb P^1$
-spectra. The reader is encouraged to skip to this section directly. Our main results in the form of Corollary 4.9, Theorem 4.14, and Corollary 4.15 can be understood without reading the rest of the article (except perhaps for taking a glance at §4.1, where some notation is introduced).
1.2 Pullbacks and the Rost–Schmid complex
The results just sketched are obtained by combining the main results of [Reference Bosch, Lütkebohmert and Raynaud2] with a technical result that we describe now. Essentially, this establishes [2, Conjecture 6.10] (for
![]() $n \ge 3$
); all our applications are a consequence of this and were already anticipated in writing [Reference Bosch, Lütkebohmert and Raynaud2].
$n \ge 3$
); all our applications are a consequence of this and were already anticipated in writing [Reference Bosch, Lütkebohmert and Raynaud2].
Let M be a strictly homotopy-invariant sheaf (see §2 for this and related notions, and a more complete account of the following sketch) and X a smooth variety. Morel has proved [18, Corollary 5.43] that there is a very convenient complex, known as the Rost–Schmid complex
![]() $C^*(X, M)$
, which can be used to compute the Nisnevich cohomology
$C^*(X, M)$
, which can be used to compute the Nisnevich cohomology
![]() $H^*(X, M)$
. This complex has the special property that
$H^*(X, M)$
. This complex has the special property that
![]() $C^n(X, M)$
depends only on the n-fold contraction
$C^n(X, M)$
depends only on the n-fold contraction
![]() $M_{-n}$
, and similarly so does the boundary map
$M_{-n}$
, and similarly so does the boundary map
![]() $C^n(X, M) \to C^{n+1}(X, M)$
. Let
$C^n(X, M) \to C^{n+1}(X, M)$
. Let
![]() $Z \subset X$
have codimension
$Z \subset X$
have codimension
![]() $\ge d$
. An obvious modification
$\ge d$
. An obvious modification
![]() $C^*_Z(X, M)$
of
$C^*_Z(X, M)$
of
![]() $C^*(X,M)$
can be used to compute
$C^*(X,M)$
can be used to compute
![]() $H^*_Z(X, M)$
; by construction one has
$H^*_Z(X, M)$
; by construction one has
![]() $C^n_Z(X, M) = 0$
for
$C^n_Z(X, M) = 0$
for
![]() $n < d$
. It follows that the group
$n < d$
. It follows that the group
![]() $H^d_Z(X, M)$
depends only on
$H^d_Z(X, M)$
depends only on
![]() $M_{-d}$
(in fact this holds for all groups
$M_{-d}$
(in fact this holds for all groups
![]() $H^*_Z(X, M)$
, but we are most interested in the lowest one). Now let
$H^*_Z(X, M)$
, but we are most interested in the lowest one). Now let
![]() $f: Y \to X$
be a morphism of smooth varieties with
$f: Y \to X$
be a morphism of smooth varieties with
![]() $f^{-1}(Z)$
also of codimension
$f^{-1}(Z)$
also of codimension
![]() $\ge d$
on Y. Then the pullback map
$\ge d$
on Y. Then the pullback map
 $$ \begin{align} f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M) \end{align} $$
$$ \begin{align} f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M) \end{align} $$
is a morphism of abelian groups, both of which depend only on
![]() $M_{-d}$
.
$M_{-d}$
.
It is not difficult to show (using the results of [Reference Bosch, Lütkebohmert and Raynaud2]; see the proof of Theorem 4.6 in this article for details) that [2, Conjecture 6.10] is equivalent to the statement that the morphism (1) also depends only on
![]() $M_{-d}$
, in an appropriate sense.Footnote
3
The main result of this article (Theorem 3.1) states that this is true.
$M_{-d}$
, in an appropriate sense.Footnote
3
The main result of this article (Theorem 3.1) states that this is true.
We establish this by adapting an argument of Levine, using a variant of Gabber’s presentation lemma to set up an induction on d. (The case
![]() $d=0$
holds tautologically.)
$d=0$
holds tautologically.)
1.3 From pullbacks to stabilization
This article brings to conclusion a program started in [Reference Bosch, Lütkebohmert and Raynaud2]. There we developed the following strategy for establishing stabilization results such as Theorem 1.1. First we note that
![]() $S^1$
-stabilization is well understood and behaves largely as in topology; thus it suffices to prove the analogous result for motivic
$S^1$
-stabilization is well understood and behaves largely as in topology; thus it suffices to prove the analogous result for motivic
![]() $S^1$
-spectra. (For detailed definitions of this and the following notions, see §4.1.) Write
$S^1$
-spectra. (For detailed definitions of this and the following notions, see §4.1.) Write
 $\mathcal {SH}^{S^1}\!(k)(d) \subset \mathcal {SH}^{S^1}\!(k)$
for the localizing subcategory generated by d-fold
$\mathcal {SH}^{S^1}\!(k)(d) \subset \mathcal {SH}^{S^1}\!(k)$
for the localizing subcategory generated by d-fold
![]() ${\mathbb {G}_m}$
-suspensions, and similarly
${\mathbb {G}_m}$
-suspensions, and similarly
![]() $\mathcal {SH}(k)^{\text {eff}}(d) \subset \mathcal {SH}(k)$
for the localizing subcategory generated by the image of
$\mathcal {SH}(k)^{\text {eff}}(d) \subset \mathcal {SH}(k)$
for the localizing subcategory generated by the image of
 $\mathcal {SH}^{S^1}\!(k)(d)$
. These categories afford t-structures induced by the canonical generating sets, and hence the stabilization functor
$\mathcal {SH}^{S^1}\!(k)(d)$
. These categories afford t-structures induced by the canonical generating sets, and hence the stabilization functor
 $\mathcal {SH}^{S^1}\!(k)(d) \to \mathcal {SH}(k)^{\text {eff}}(d)$
is right-t-exact. One finds that in order to prove stabilization results, it will be enough to show that the induced functor on hearts
$\mathcal {SH}^{S^1}\!(k)(d) \to \mathcal {SH}(k)^{\text {eff}}(d)$
is right-t-exact. One finds that in order to prove stabilization results, it will be enough to show that the induced functor on hearts
 $\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit \to \mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit $
is an equivalence. Since the right-hand category is by now well understood, let us focus on the left-hand side. It is not difficult to show that the functor of d-fold
$\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit \to \mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit $
is an equivalence. Since the right-hand category is by now well understood, let us focus on the left-hand side. It is not difficult to show that the functor of d-fold
![]() ${\mathbb {G}_m}$
-loops
${\mathbb {G}_m}$
-loops
 $\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit \to \mathcal {SH}^{S^1}\!(k)^\heartsuit \simeq \mathbf {HI}(k)$
is monadic. In other words, we may think of objects of
$\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit \to \mathcal {SH}^{S^1}\!(k)^\heartsuit \simeq \mathbf {HI}(k)$
is monadic. In other words, we may think of objects of
 $\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
as strictly homotopy-invariant sheaves with extra structure. One way of phrasing the main result of [Reference Bosch, Lütkebohmert and Raynaud2] is (see, e.g., [2, Remark 4.17]) that this extra structure is precisely the data of closed pullbacks on cohomology with support in codimension d. These are precisely the kinds of maps that we show depend only on
$\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
as strictly homotopy-invariant sheaves with extra structure. One way of phrasing the main result of [Reference Bosch, Lütkebohmert and Raynaud2] is (see, e.g., [2, Remark 4.17]) that this extra structure is precisely the data of closed pullbacks on cohomology with support in codimension d. These are precisely the kinds of maps that we show depend only on
![]() $M_{-d}$
‘in an appropriate sense’. To be more specific, the appropriate sense is that
$M_{-d}$
‘in an appropriate sense’. To be more specific, the appropriate sense is that
![]() $M_{-d}$
is a so-called sheaf with
$M_{-d}$
is a so-called sheaf with
![]() $\mathbb A^1$
-transfers (see Remark 3.2 for details), and the pullback depends only on this additional structure.
$\mathbb A^1$
-transfers (see Remark 3.2 for details), and the pullback depends only on this additional structure.
All of this more or less impliesFootnote
4
that
 $\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
is equivalent to the full subcategory of the category of sheaves with
$\mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
is equivalent to the full subcategory of the category of sheaves with
![]() $\mathbb A^1$
-transfers on objects of the form
$\mathbb A^1$
-transfers on objects of the form
![]() $M_{-d}$
. It follows from [2, Theorem 5.19] that for d big enough, this subcategory is equivalent to
$M_{-d}$
. It follows from [2, Theorem 5.19] that for d big enough, this subcategory is equivalent to
![]() $\mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit $
, as desired.
$\mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit $
, as desired.
1.4 Notation and conventions
We fix throughout a field k. All nontrivial results will require k to be perfect.
Given a presheaf M on the category of smooth varieties over k, and an essentially smooth k-scheme X, we denote by
![]() $M(X)$
the evaluation at X of the canonical extension of M to pro-(smooth schemes), into which the category of essentially smooth schemes embeds by [8, Proposition 8.13.5]. In other words, if
$M(X)$
the evaluation at X of the canonical extension of M to pro-(smooth schemes), into which the category of essentially smooth schemes embeds by [8, Proposition 8.13.5]. In other words, if
![]() $X = \operatorname *{\mathrm {lim}}_i X_i$
is a cofiltered limit of smooth k-schemes with affine transition maps, then
$X = \operatorname *{\mathrm {lim}}_i X_i$
is a cofiltered limit of smooth k-schemes with affine transition maps, then
![]() $M(X) = \operatorname *{\mathrm {colim}}_i M(X_i)$
(and this is known to be independent of the presentation of X).
$M(X) = \operatorname *{\mathrm {colim}}_i M(X_i)$
(and this is known to be independent of the presentation of X).
Given a scheme X and a point
![]() $x \in X$
, we identify x and
$x \in X$
, we identify x and
![]() $\mathrm {Spec}(k(x))$
. In particular, if X is smooth and k is perfect (so that x is essentially smooth), then we write
$\mathrm {Spec}(k(x))$
. In particular, if X is smooth and k is perfect (so that x is essentially smooth), then we write
![]() $M(x)$
for what is often denoted
$M(x)$
for what is often denoted
![]() $M(k(x))$
.
$M(k(x))$
.
Given a scheme X and
![]() $d \ge 0$
, we write
$d \ge 0$
, we write
![]() $X^{(d)}$
for the set of points of X of codimension d on X; in other words, if
$X^{(d)}$
for the set of points of X of codimension d on X; in other words, if
![]() $x \in X$
, then
$x \in X$
, then
![]() $x \in X^{(d)}$
if and only if
$x \in X^{(d)}$
if and only if
![]() $\dim X_x = d$
, where
$\dim X_x = d$
, where
![]() $X_x$
denotes the localization of X in x. For example,
$X_x$
denotes the localization of X in x. For example,
![]() $X^{(0)}$
is the set of generic points of X.
$X^{(0)}$
is the set of generic points of X.
For a regular immersion
![]() $Y \hookrightarrow X$
, we denote by
$Y \hookrightarrow X$
, we denote by
![]() $N_{Y/X}$
the normal bundle and by
$N_{Y/X}$
the normal bundle and by
 $\omega _{Y/X} = \det N_{Y/X}^{\vee }$
the determinant of the conormal bundle. More generally, for any morphism
$\omega _{Y/X} = \det N_{Y/X}^{\vee }$
the determinant of the conormal bundle. More generally, for any morphism
![]() $Y \to X$
such that the cotangent complex
$Y \to X$
such that the cotangent complex
![]() $L_{Y/X}$
is perfect, we write
$L_{Y/X}$
is perfect, we write
![]() $\omega _{Y/X} = \det L_{Y/X}$
.
$\omega _{Y/X} = \det L_{Y/X}$
.
2 Preliminaries
We recall some well-known results from motivic homotopy theory.
2.1 Strictly homotopy-invariant sheaves
We write
![]() ${\mathrm {S}\mathrm {m}}_k$
for the category of smooth k-schemes. We make it into a site by endowing it with the Nisnevich topology [Reference Nisnevich20]. This is the only topology we shall use; all cohomology will be with respect to it. Unless noted otherwise, by a (pre)sheaf we mean a (pre)sheaf of abelian groups on
${\mathrm {S}\mathrm {m}}_k$
for the category of smooth k-schemes. We make it into a site by endowing it with the Nisnevich topology [Reference Nisnevich20]. This is the only topology we shall use; all cohomology will be with respect to it. Unless noted otherwise, by a (pre)sheaf we mean a (pre)sheaf of abelian groups on
![]() ${\mathrm {S}\mathrm {m}}_k$
.
${\mathrm {S}\mathrm {m}}_k$
.
Recall that a sheaf M is called strictly homotopy invariant if, for all
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
, the canonical map
$X \in {\mathrm {S}\mathrm {m}}_k$
, the canonical map
 $H^*(X, M) \to H^*\left (\mathbb A^1 \times X, M\right )$
is an isomorphism. We denote the category of strictly homotopy-invariant sheaves by
$H^*(X, M) \to H^*\left (\mathbb A^1 \times X, M\right )$
is an isomorphism. We denote the category of strictly homotopy-invariant sheaves by
![]() $\mathbf {HI}(k)$
.
$\mathbf {HI}(k)$
.
Example 2.1. For a commutative ring A, denote by
![]() $GW(A)$
its Grothendieck–Witt ring – that is, the additive group completion of the semiring of isometry classes of nondegenerate, symmetric bilinear forms on A [Reference Milnor and Husemoller14]. Write
$GW(A)$
its Grothendieck–Witt ring – that is, the additive group completion of the semiring of isometry classes of nondegenerate, symmetric bilinear forms on A [Reference Milnor and Husemoller14]. Write
![]() $\underline {GW}$
for the associated Nisnevich sheaf on
$\underline {GW}$
for the associated Nisnevich sheaf on
![]() ${\mathrm {S}\mathrm {m}}_k$
. Then
${\mathrm {S}\mathrm {m}}_k$
. Then
![]() $\underline {GW}$
turns out to be strictly homotopy invariant (combine [21, Theorem A] and [18, §§2,3]).
$\underline {GW}$
turns out to be strictly homotopy invariant (combine [21, Theorem A] and [18, §§2,3]).
Remark 2.2. As mentioned in the introduction, there exists a universal homotopy theory built out of (pointed) smooth varieties by enforcing
![]() $\mathbb A^1$
-homotopy invariance and Nisnevich descent [Reference Morel and Voevodsky19]; we denote it by
$\mathbb A^1$
-homotopy invariance and Nisnevich descent [Reference Morel and Voevodsky19]; we denote it by
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
. By construction, for
$\mathcal {S}\mathrm {pc}{}(k)_*$
. By construction, for
![]() $M \in \mathbf {HI}(k)$
, the Eilenberg–MacLane spaces
$M \in \mathbf {HI}(k)$
, the Eilenberg–MacLane spaces
![]() $K(M, i)$
define objects in
$K(M, i)$
define objects in
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
. In this way, results about
$\mathcal {S}\mathrm {pc}{}(k)_*$
. In this way, results about
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
translate into properties of the cohomology of strictly homotopy-invariant sheaves. For example, given
$\mathcal {S}\mathrm {pc}{}(k)_*$
translate into properties of the cohomology of strictly homotopy-invariant sheaves. For example, given
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and
$X \in {\mathrm {S}\mathrm {m}}_k$
and
![]() $Z \subset X$
closed, we have an isomorphism
$Z \subset X$
closed, we have an isomorphism
 $$ \begin{align*} H^i_Z(X,M) \simeq [X/X \setminus Z, K(M,i)]_{\mathcal{S}\mathrm{pc}{}(k)_*}, \end{align*} $$
$$ \begin{align*} H^i_Z(X,M) \simeq [X/X \setminus Z, K(M,i)]_{\mathcal{S}\mathrm{pc}{}(k)_*}, \end{align*} $$
and given a morphism
![]() $f: Y \to X$
(resp., a closed subset
$f: Y \to X$
(resp., a closed subset
![]() $Z' \subset Z$
) we have morphisms
$Z' \subset Z$
) we have morphisms
![]() $Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z$
(resp.,
$Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z$
(resp.,
![]() $X/X \setminus Z \to X/X \setminus Z'$
) inducing the pullback
$X/X \setminus Z \to X/X \setminus Z'$
) inducing the pullback
 $H^i_Z(X, M) \to H^i_{f^{-1}(Z)}(Y, M)$
(resp., the extension of the support map
$H^i_Z(X, M) \to H^i_{f^{-1}(Z)}(Y, M)$
(resp., the extension of the support map
![]() $H^i_{Z'}(X, M) \to H^i_Z(X,M)$
). We will use this correspondence freely in the sequel.
$H^i_{Z'}(X, M) \to H^i_Z(X,M)$
). We will use this correspondence freely in the sequel.
2.1.1 Unramifiedness
Let
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
be connected and
$X \in {\mathrm {S}\mathrm {m}}_k$
be connected and
![]() $\emptyset \ne U \subset X$
be open. Then for
$\emptyset \ne U \subset X$
be open. Then for
![]() $M \in \mathbf {HI}(k)$
, the canonical map
$M \in \mathbf {HI}(k)$
, the canonical map
![]() $M(X) \to M(U)$
is an injection [17, Lemma 6.4.4]. It follows that if
$M(X) \to M(U)$
is an injection [17, Lemma 6.4.4]. It follows that if
![]() $\xi \in X$
is the generic point, then
$\xi \in X$
is the generic point, then
![]() $M(X) \hookrightarrow M(\xi )$
.
$M(X) \hookrightarrow M(\xi )$
.
2.1.2 Contractions
For a presheaf M, write
![]() $M_{-1}$
for the presheaf given by
$M_{-1}$
for the presheaf given by
 $M_{-1}(X) = \mathrm {ker}\left (M\left (\left (\mathbb A^1 \setminus 0\right ) \times X\right ) \xrightarrow {i_1^*} M(X)\right )$
and
$M_{-1}(X) = \mathrm {ker}\left (M\left (\left (\mathbb A^1 \setminus 0\right ) \times X\right ) \xrightarrow {i_1^*} M(X)\right )$
and
![]() $M_{-n}$
for the n-fold iteration of this construction. Here
$M_{-n}$
for the n-fold iteration of this construction. Here
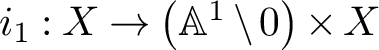 $i_1: X \to \left (\mathbb A^1 \setminus 0\right ) \times X$
denotes the inclusion at
$i_1: X \to \left (\mathbb A^1 \setminus 0\right ) \times X$
denotes the inclusion at
![]() $1 \in \mathbb A^1$
. Pullback along the structure map splits
$1 \in \mathbb A^1$
. Pullback along the structure map splits
![]() $i_1^*$
, and hence
$i_1^*$
, and hence
![]() $M_{-1}$
is a summand of the internal mapping object
$M_{-1}$
is a summand of the internal mapping object
 $\underline {\operatorname {Hom}}\left (\mathbb A^1 \setminus 0, M\right )$
. It follows that
$\underline {\operatorname {Hom}}\left (\mathbb A^1 \setminus 0, M\right )$
. It follows that
![]() $M_{-n}$
is a ((strictly) homotopy-invariant) (pre)sheaf if M is.
$M_{-n}$
is a ((strictly) homotopy-invariant) (pre)sheaf if M is.
Example 2.3. We have
 $H^1\left (\mathbb P^1_K, M\right ) \simeq M_{-1}(K)$
, for any finitely generated separable field extension
$H^1\left (\mathbb P^1_K, M\right ) \simeq M_{-1}(K)$
, for any finitely generated separable field extension
![]() $K/k$
. Indeed, we can cover
$K/k$
. Indeed, we can cover
![]() $\mathbb P^1_K$
by two copies of
$\mathbb P^1_K$
by two copies of
![]() $\mathbb A^1_K$
with intersection
$\mathbb A^1_K$
with intersection
 $\left (\mathbb A^1 \setminus 0\right )_K$
and
$\left (\mathbb A^1 \setminus 0\right )_K$
and
 $H^i\left (\mathbb A^1_K, M\right ) \simeq H^i(\mathrm {Spec}(K), M)$
(whence in particular
$H^i\left (\mathbb A^1_K, M\right ) \simeq H^i(\mathrm {Spec}(K), M)$
(whence in particular
 $H^1\left (\mathbb A^1_K, M\right ) = 0$
), so the claim follows from the Mayer–Vietoris sequence for this covering.
$H^1\left (\mathbb A^1_K, M\right ) = 0$
), so the claim follows from the Mayer–Vietoris sequence for this covering.
2.1.3
 $GW$
-module structure
$GW$
-module structure
Set
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and
$X \in {\mathrm {S}\mathrm {m}}_k$
and
![]() $u \in \mathcal O(X)^\times $
. Multiplication by u defines an endomorphism of
$u \in \mathcal O(X)^\times $
. Multiplication by u defines an endomorphism of
 $\left (\mathbb A^1 \setminus 0\right ) \times X$
and hence of
$\left (\mathbb A^1 \setminus 0\right ) \times X$
and hence of
 $\underline {\operatorname {Hom}}\left (\mathbb A^1 \setminus 0, M\right )(X)$
; passing to the summand, we obtain
$\underline {\operatorname {Hom}}\left (\mathbb A^1 \setminus 0, M\right )(X)$
; passing to the summand, we obtain
![]() $\left \langle u \right \rangle : M_{-1}(X) \to M_{-1}(X)$
. Suppose that
$\left \langle u \right \rangle : M_{-1}(X) \to M_{-1}(X)$
. Suppose that
![]() $M \in \mathbf {HI}(k)$
. Since the map
$M \in \mathbf {HI}(k)$
. Since the map
![]() $\mathbb {Z}\left [\mathcal O^\times \right ] \to \underline {GW}, u \mapsto \left \langle u \right \rangle $
, is surjective on fields, unramifiedness implies that this construction extends in at most one way to a
$\mathbb {Z}\left [\mathcal O^\times \right ] \to \underline {GW}, u \mapsto \left \langle u \right \rangle $
, is surjective on fields, unramifiedness implies that this construction extends in at most one way to a
![]() $\underline {GW}$
-module structure on
$\underline {GW}$
-module structure on
![]() $M_{-1}$
. It turns out that this
$M_{-1}$
. It turns out that this
![]() $\underline {GW}$
-module structure always exists [18, Lemma 3.49].
$\underline {GW}$
-module structure always exists [18, Lemma 3.49].
2.1.4 Twisting
Given a line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
, write
$X \in {\mathrm {S}\mathrm {m}}_k$
, write
![]() $\mathcal L^\times $
for the sheaf of nonvanishing sections. For
$\mathcal L^\times $
for the sheaf of nonvanishing sections. For
![]() $M \in \mathbf {HI}(k)$
and
$M \in \mathbf {HI}(k)$
and
![]() $d> 0$
, we put
$d> 0$
, we put
![]() $M_{-d}(X, \mathcal L) = H^0\left (X, M_{-d} \times _{\mathcal O^\times } \mathcal L^\times \right )$
; here the action of
$M_{-d}(X, \mathcal L) = H^0\left (X, M_{-d} \times _{\mathcal O^\times } \mathcal L^\times \right )$
; here the action of
![]() $\mathcal O^\times $
on
$\mathcal O^\times $
on
![]() $M_{-d}$
is via
$M_{-d}$
is via
![]() $\mathcal O^\times \to \underline {GW}$
, and the action on
$\mathcal O^\times \to \underline {GW}$
, and the action on
![]() $\mathcal L^\times $
is given by multiplication. Note that since
$\mathcal L^\times $
is given by multiplication. Note that since
 $\left \langle u \right \rangle = \left \langle u^{-1} \right \rangle $
, we have
$\left \langle u \right \rangle = \left \langle u^{-1} \right \rangle $
, we have
 $M_{-d}(X, \mathcal L) \simeq M_{-d}\left (X, \mathcal L^{-1}\right )$
.
$M_{-d}(X, \mathcal L) \simeq M_{-d}\left (X, \mathcal L^{-1}\right )$
.
2.1.5 Thom spaces
For
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and V a vector bundle on X of rank d, we have
$X \in {\mathrm {S}\mathrm {m}}_k$
and V a vector bundle on X of rank d, we have
![]() $Th(V) := V/V \setminus 0_X \in \mathcal {S}\mathrm {pc}{}(k)_*$
. For
$Th(V) := V/V \setminus 0_X \in \mathcal {S}\mathrm {pc}{}(k)_*$
. For
![]() $M \in \mathbf {HI}(k)$
, there are canonical isomorphisms [18, Lemma 5.35]
$M \in \mathbf {HI}(k)$
, there are canonical isomorphisms [18, Lemma 5.35]
 $$ \begin{align*} [V/V \setminus 0_X, K(M, d)]_{\mathcal{S}\mathrm{pc}{}(k)_*} \simeq H^d_{0_X}(V, M) \simeq M_{-d}(X, \det V). \end{align*} $$
$$ \begin{align*} [V/V \setminus 0_X, K(M, d)]_{\mathcal{S}\mathrm{pc}{}(k)_*} \simeq H^d_{0_X}(V, M) \simeq M_{-d}(X, \det V). \end{align*} $$
2.1.6 Homotopy purity
Set
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and
$X \in {\mathrm {S}\mathrm {m}}_k$
and
![]() $U \subset X$
open, with reduced closed complement
$U \subset X$
open, with reduced closed complement
![]() $Z = X \setminus U$
also smooth. Then in
$Z = X \setminus U$
also smooth. Then in
![]() $\mathcal {S}\mathrm {pc}{}(k)_*$
there is a canonical equivalence [19, §3 Theorem 2.23]
$\mathcal {S}\mathrm {pc}{}(k)_*$
there is a canonical equivalence [19, §3 Theorem 2.23]
 $$ \begin{align*} X/X \setminus Z \simeq Th\left(N_{Z/X}\right). \end{align*} $$
$$ \begin{align*} X/X \setminus Z \simeq Th\left(N_{Z/X}\right). \end{align*} $$
2.1.7 Boundary maps
Set
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and
$X \in {\mathrm {S}\mathrm {m}}_k$
and
![]() $x \in X^{(d)}$
. Then
$x \in X^{(d)}$
. Then
![]() $X_x$
is an essentially smooth scheme with closed point x. Homotopy purity supplies us with the collapse sequenceFootnote
5
$X_x$
is an essentially smooth scheme with closed point x. Homotopy purity supplies us with the collapse sequenceFootnote
5
 $$ \begin{align*} X_x \to X_x/X_x \setminus x \simeq Th\left(N_{x/X}\right) \xrightarrow{\partial} \Sigma(X_x \setminus x). \end{align*} $$
$$ \begin{align*} X_x \to X_x/X_x \setminus x \simeq Th\left(N_{x/X}\right) \xrightarrow{\partial} \Sigma(X_x \setminus x). \end{align*} $$
Pullback along
![]() $\partial $
induces the boundary map in the long exact sequence of cohomology with support. We most commonly use the case where
$\partial $
induces the boundary map in the long exact sequence of cohomology with support. We most commonly use the case where
![]() $d=1$
. Then
$d=1$
. Then
![]() $X_x \setminus x = \xi $
, where
$X_x \setminus x = \xi $
, where
![]() $\xi $
is the generic point of X (specializing to x), and the boundary map takes the familiar form
$\xi $
is the generic point of X (specializing to x), and the boundary map takes the familiar form
 $$ \begin{align*} \partial: M(\xi) \to M_{-1}\left(x, \omega_{x/X}\right). \end{align*} $$
$$ \begin{align*} \partial: M(\xi) \to M_{-1}\left(x, \omega_{x/X}\right). \end{align*} $$
2.1.8 Monogeneic transfers
Let k be perfect and
![]() $K/k$
be a finitely generated field extension, whence
$K/k$
be a finitely generated field extension, whence
![]() $X = \mathrm {Spec}(K)$
is an essentially smooth scheme. Let
$X = \mathrm {Spec}(K)$
is an essentially smooth scheme. Let
![]() $K(x)/K$
be a finite, monogeneic field extension. We are supplied with an embedding
$K(x)/K$
be a finite, monogeneic field extension. We are supplied with an embedding
 , and thus homotopy purity provides us with a collapse map
, and thus homotopy purity provides us with a collapse map
 $$ \begin{align*} \mathbb P^1_X \to \mathbb P^1_X/\mathbb P^1_X \setminus X^{\prime} \simeq Th\left(N_{X^{\prime}/\mathbb A^1_X}\right) \simeq Th\left(\mathcal O_{X^{\prime}}\right); \end{align*} $$
$$ \begin{align*} \mathbb P^1_X \to \mathbb P^1_X/\mathbb P^1_X \setminus X^{\prime} \simeq Th\left(N_{X^{\prime}/\mathbb A^1_X}\right) \simeq Th\left(\mathcal O_{X^{\prime}}\right); \end{align*} $$
here the normal bundle is canonically trivialized by the minimal polynomial of x. Pullback along this collapse map induces the monogeneic transfer Footnote 6 [18, p.99]
Slightly more generally, suppose that
![]() $z \in \mathbb P^1_K$
is any closed point. Then we have the transfer map
$z \in \mathbb P^1_K$
is any closed point. Then we have the transfer map
 $$ \begin{align*} \mathrm{tr}_z: M_{-1}\left(z, \omega_{z/\mathbb P^1_K}\right) \simeq H^1_z\left(\mathbb P^1_K, M\right) \to H^1\left(\mathbb P^1_K, M\right) \simeq M_{-1}(K). \end{align*} $$
$$ \begin{align*} \mathrm{tr}_z: M_{-1}\left(z, \omega_{z/\mathbb P^1_K}\right) \simeq H^1_z\left(\mathbb P^1_K, M\right) \to H^1\left(\mathbb P^1_K, M\right) \simeq M_{-1}(K). \end{align*} $$
This contains no new information: if
![]() $z \in \mathbb A^1_K$
, then
$z \in \mathbb A^1_K$
, then
![]() $\mathrm {tr}_z$
coincides up to isomorphism with
$\mathrm {tr}_z$
coincides up to isomorphism with
![]() $\tau _z$
, and the only other case is
$\tau _z$
, and the only other case is
![]() $z = \infty $
, which is a rational point, so
$z = \infty $
, which is a rational point, so
![]() $\mathrm {tr}_z$
is isomorphic to the identity.
$\mathrm {tr}_z$
is isomorphic to the identity.
2.2 Cousin and Rost–Schmid complexes
Let M be a sheaf of abelian groups on X. The cohomology of M on X can be computed using the coniveau spectral sequence (see, e.g., [3, §1]). On the zero line of the
![]() $E_1$
page one finds the so-called Cousin complex [3, (1.3)]:
$E_1$
page one finds the so-called Cousin complex [3, (1.3)]:
 $$ \begin{align} M(X) \to \bigoplus_{x \in X^{(0)}} M(x) \to \bigoplus_{x \in X^{(1)}} H^1_x(X, M) \to \cdots \to \bigoplus_{x \in X^{(d)}} H^d_x(X, M) =: C^d(X, M) \to \cdots. \end{align} $$
$$ \begin{align} M(X) \to \bigoplus_{x \in X^{(0)}} M(x) \to \bigoplus_{x \in X^{(1)}} H^1_x(X, M) \to \cdots \to \bigoplus_{x \in X^{(d)}} H^d_x(X, M) =: C^d(X, M) \to \cdots. \end{align} $$
Here
 $$ \begin{align} H^d_x(X, M) = \operatorname*{\mathrm{colim}}_{V \ni x} H^d_{\overline{\{x\}} \cap V}(V, X), \end{align} $$
$$ \begin{align} H^d_x(X, M) = \operatorname*{\mathrm{colim}}_{V \ni x} H^d_{\overline{\{x\}} \cap V}(V, X), \end{align} $$
where the colimit runs over open neighborhoods of x. The boundary maps in formula (2) are induced by certain boundary maps in long exact sequences of cohomology with support.
Now suppose that
![]() $M \in \mathbf {HI}(k)$
. By the Bloch–Ogus–Gabber theorem [3, Theorem 6.2.1], the Cousin complex (2) is then exact when viewed as a complex of sheaves (i.e., for X local). Since it consists of flasque sheafes, it can thus be used to compute the Zariski cohomology of M. The terms also turn out to be Nisnevich-acyclic (see [3, Theorem 8.3.1] or [18, Lemma 5.42]), and hence the Cousin complex computes the Nisnevich cohomology of M as well (which thus turns out to coincide with the Zariski cohomology).
$M \in \mathbf {HI}(k)$
. By the Bloch–Ogus–Gabber theorem [3, Theorem 6.2.1], the Cousin complex (2) is then exact when viewed as a complex of sheaves (i.e., for X local). Since it consists of flasque sheafes, it can thus be used to compute the Zariski cohomology of M. The terms also turn out to be Nisnevich-acyclic (see [3, Theorem 8.3.1] or [18, Lemma 5.42]), and hence the Cousin complex computes the Nisnevich cohomology of M as well (which thus turns out to coincide with the Zariski cohomology).
Remark 2.4. The Cousin complex can also be used to compute cohomology with support in a closed subscheme Z; just replace
 $$ \begin{align*} C^d(X, M) = \bigoplus_{x \in X^{(d)}} H^d_x(X, M) \quad\text{by}\quad C^d_Z(X, M) = \bigoplus_{x \in X^{(d)} \cap Z} H^d_x(X, M). \end{align*} $$
$$ \begin{align*} C^d(X, M) = \bigoplus_{x \in X^{(d)}} H^d_x(X, M) \quad\text{by}\quad C^d_Z(X, M) = \bigoplus_{x \in X^{(d)} \cap Z} H^d_x(X, M). \end{align*} $$
This holds, since the resolving sheaves are flasque.
Now let k be perfect. We would like to make this complex more explicit. As a first step, homotopy purity (see §§2.1.5 and 2.1.6) allows us to identify the groups (3) in the Cousin complex more explicitly as
 $$ \begin{align*} H^d_x(X, M) \simeq M_{-d}\left(x, \omega_{x/X}\right). \end{align*} $$
$$ \begin{align*} H^d_x(X, M) \simeq M_{-d}\left(x, \omega_{x/X}\right). \end{align*} $$
Indeed, by generic smoothness, shrinking V if necessary, we may assume that
![]() $Z := \overline {\{x\}} \cap V$
is smooth of codimension d on V, and then
$Z := \overline {\{x\}} \cap V$
is smooth of codimension d on V, and then
 $$ \begin{align*} H^d_Z(V, M) \simeq [V/V \setminus Z, K(d,M)] \simeq \left[Th\left(N_{Z/V}\right), K(d,M)\right] \simeq M_{-d}\left(Z, \omega_{Z/V}\right); \end{align*} $$
$$ \begin{align*} H^d_Z(V, M) \simeq [V/V \setminus Z, K(d,M)] \simeq \left[Th\left(N_{Z/V}\right), K(d,M)\right] \simeq M_{-d}\left(Z, \omega_{Z/V}\right); \end{align*} $$
the claim now follows by taking colimits. The boundary maps of the Cousin complex can also be identified. We only use the following weak form of this result:
Theorem 2.5. Morel [Reference Morel18]
Set
![]() $M \in \mathbf {HI}(k)$
,
$M \in \mathbf {HI}(k)$
,
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
, and
$X \in {\mathrm {S}\mathrm {m}}_k$
, and
![]() $d \ge 0$
. Then the boundary map
$d \ge 0$
. Then the boundary map
![]() $C^d(X, M) \to C^{d+1}(X, M)$
in the Cousin complex depends only on the sheaf
$C^d(X, M) \to C^{d+1}(X, M)$
in the Cousin complex depends only on the sheaf
![]() $M_{-d}$
, together with (if
$M_{-d}$
, together with (if
![]() $d>0$
) its structure as a
$d>0$
) its structure as a
![]() $\underline {GW}$
-module from §2.1.3.
$\underline {GW}$
-module from §2.1.3.
In fact, Morel proves this result by identifying the Cousin complex with another complex called the Rost–Schmid complex (which has the same terms but a priori different boundary maps). In other words, the boundary map in the Cousin complex admits an explicit formula, involving only the codimension
![]() $1$
boundary of §2.1.7 and (composites of) the monogeneic transfer of §2.1.8.Footnote
7
$1$
boundary of §2.1.7 and (composites of) the monogeneic transfer of §2.1.8.Footnote
7
In the sequel, we will not distinguish between the Cousin and Rost–Schmid complexes.
3 A ‘formula’ for closed pullback
In this section we establish our main result.
Theorem 3.1. Let k be a perfect field and set
![]() $M \in \mathbf {HI}(k)$
,
$M \in \mathbf {HI}(k)$
,
![]() $f: Y \to X \in {\mathrm {S}\mathrm {m}}_k$
,
$f: Y \to X \in {\mathrm {S}\mathrm {m}}_k$
,
![]() $d \ge 1$
, and
$d \ge 1$
, and
![]() $Z \subset X$
closed of codimension
$Z \subset X$
closed of codimension
![]() $\ge d$
such that
$\ge d$
such that
![]() $f^{-1}(Z) \subset Y$
is also of codimension
$f^{-1}(Z) \subset Y$
is also of codimension
![]() $\ge d$
. Then the map
$\ge d$
. Then the map
 $$ \begin{align*} f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M) \end{align*} $$
$$ \begin{align*} f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M) \end{align*} $$
depends only on
![]() $M_{-d} \in \mathbf {HI}(k)$
, together with its
$M_{-d} \in \mathbf {HI}(k)$
, together with its
![]() $GW$
-module structure and transfers along monogeneic field extensions (in the sense of §§2.1.3 and 2.1.8).
$GW$
-module structure and transfers along monogeneic field extensions (in the sense of §§2.1.3 and 2.1.8).
In the sequel, we shall say ‘depends only on
![]() $M_{-d}$
’ to mean what is asserted in the theorem – that is, ‘depends only on
$M_{-d}$
’ to mean what is asserted in the theorem – that is, ‘depends only on
![]() $M_{-d}$
as a
$M_{-d}$
as a
![]() $GW$
-module with transfers’.
$GW$
-module with transfers’.
Remark 3.2. Let us make precise the notion that ‘
![]() $f^*$
depends only on
$f^*$
depends only on
![]() $M_{-d}$
’.
$M_{-d}$
’.
For this, first recall from [Reference Bosch, Lütkebohmert and Raynaud2, §5.1] the notion of a presheaf with
![]() $\mathbb A^1$
-transfers. This is just a presheaf F on
$\mathbb A^1$
-transfers. This is just a presheaf F on
![]() ${\mathrm {S}\mathrm {m}}_k$
together with, for every finitely generated field
${\mathrm {S}\mathrm {m}}_k$
together with, for every finitely generated field
![]() $K/k$
, a
$K/k$
, a
![]() $GW(K)$
-module structure on
$GW(K)$
-module structure on
![]() $F(K)$
, and for every finite monogeneic extension
$F(K)$
, and for every finite monogeneic extension
![]() $K(x)/K$
, a transfer
$K(x)/K$
, a transfer
![]() $\tau _x: F(K(x)) \to F(K)$
. A morphism of presheaves with
$\tau _x: F(K(x)) \to F(K)$
. A morphism of presheaves with
![]() $\mathbb A^1$
-transfers is a morphisms of sheaves which commutes with the
$\mathbb A^1$
-transfers is a morphisms of sheaves which commutes with the
![]() $GW(K)$
-module structures and the transfers. If
$GW(K)$
-module structures and the transfers. If
![]() $M \in \mathbf {HI}(k)$
and
$M \in \mathbf {HI}(k)$
and
![]() $d \ge 1$
, then
$d \ge 1$
, then
![]() $M_{-d}$
acquires the structure of a presheaf with
$M_{-d}$
acquires the structure of a presheaf with
![]() $\mathbb A^1$
-transfers (see §§2.1.3 and 2.1.8 or [Reference Bosch, Lütkebohmert and Raynaud2, Example 5.2]).
$\mathbb A^1$
-transfers (see §§2.1.3 and 2.1.8 or [Reference Bosch, Lütkebohmert and Raynaud2, Example 5.2]).
Now suppose we are given
![]() $M, N \in \mathbf {HI}(k)$
, and an isomorphism
$M, N \in \mathbf {HI}(k)$
, and an isomorphism
![]() $M_{-d} \simeq N_{-d}$
of presheaves with
$M_{-d} \simeq N_{-d}$
of presheaves with
![]() $\mathbb A^1$
-transfers. Then there is a canonical induced isomorphism
$\mathbb A^1$
-transfers. Then there is a canonical induced isomorphism
![]() $H^d_Z(X, M) \simeq H^d_Z(X, N)$
(and similarly for Y), by identifying the Rost–Schmid resolutions with support in Z (i.e., using Remark 2.4 and Theorem 2.5; this does not even depend on the identification of the transfers). The theorem asserts that this isomorphism is compatible with the pullback
$H^d_Z(X, M) \simeq H^d_Z(X, N)$
(and similarly for Y), by identifying the Rost–Schmid resolutions with support in Z (i.e., using Remark 2.4 and Theorem 2.5; this does not even depend on the identification of the transfers). The theorem asserts that this isomorphism is compatible with the pullback
![]() $f^*$
(and for this we crucially need the compatibility of the transfers).
$f^*$
(and for this we crucially need the compatibility of the transfers).
Remark 3.3. Note that the Rost–Schmid complex is functorial in smooth morphisms in an obvious way, so that the theorem is clear, for example, for f an open immersion. We will often use this in conjunction with the observation (which follows, e.g., from the form of the Rost–Schmid complex) that if Z has codimension
![]() $\ge d$
on X, then
$\ge d$
on X, then
 $$ \begin{align*} H^d_Z(X, M) \hookrightarrow \bigoplus_z H^d_z(X_z, M), \end{align*} $$
$$ \begin{align*} H^d_Z(X, M) \hookrightarrow \bigoplus_z H^d_z(X_z, M), \end{align*} $$
where the sum is over the (finitely many) generic points of Z of codimension d on X.
If the support is smooth and the intersection is transverse, all is well.
Lemma 3.4. Suppose that both Z and
![]() $f^{-1}(Z)$
(with its induced scheme structure as a pullback) are smooth. Then
$f^{-1}(Z)$
(with its induced scheme structure as a pullback) are smooth. Then
 $f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
depends only on
$f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
depends only on
![]() $M_{-d}$
.
$M_{-d}$
.
Proof. Since Z is smooth (and so is X), we may write
![]() $Z = Z_0 \coprod Z_1$
, where all components of
$Z = Z_0 \coprod Z_1$
, where all components of
![]() $Z_0$
have codimension precisely d on X and all components of
$Z_0$
have codimension precisely d on X and all components of
![]() $Z_1$
have codimension
$Z_1$
have codimension
![]() $>d$
. Consider the commutative diagram
$>d$
. Consider the commutative diagram

Here the vertical maps are extension of support, and hence depend only on
![]() $M_{-d}$
. Moreover, by construction the left-hand vertical map is an isomorphism. We may thus replace Z by
$M_{-d}$
. Moreover, by construction the left-hand vertical map is an isomorphism. We may thus replace Z by
![]() $Z_0$
– that is, assume that all components of Z have codimension precisely d on X.
$Z_0$
– that is, assume that all components of Z have codimension precisely d on X.
Recall from Remark 2.2 that the pullback
 $f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
is induced by pullback along the map
$f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
is induced by pullback along the map
![]() $Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z \in \mathcal {S}\mathrm {pc}{}(k)_*$
on
$Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z \in \mathcal {S}\mathrm {pc}{}(k)_*$
on
![]() $K(d,M)$
. Let
$K(d,M)$
. Let
![]() $\eta $
be a generic point of
$\eta $
be a generic point of
![]() $f^{-1}(Z)$
(necessarily of codimension d on Y). Shrinking X around
$f^{-1}(Z)$
(necessarily of codimension d on Y). Shrinking X around
![]() $f(\eta )$
using Remark 3.3, we may assume that the normal bundle
$f(\eta )$
using Remark 3.3, we may assume that the normal bundle
![]() $N_{Z/X}$
is trivial. Since
$N_{Z/X}$
is trivial. Since
 $f: \left (Y, f^{-1}(Z)\right ) \to (X, Z)$
is a morphism of smooth closed pairs [Reference Hoyois9, §3.5], the map
$f: \left (Y, f^{-1}(Z)\right ) \to (X, Z)$
is a morphism of smooth closed pairs [Reference Hoyois9, §3.5], the map
![]() $Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z$
is equivalent to
$Y/Y \setminus f^{-1}(Z) \to X/X \setminus Z$
is equivalent to
![]() $Th(g)$
, where
$Th(g)$
, where
![]() $g: N_{f^{-1}(Z)/Y} \to N_{Z/X}$
is the map induced by f [Reference Hoyois9, Theorem 3.23]. Our assumptions on codimension imply that
$g: N_{f^{-1}(Z)/Y} \to N_{Z/X}$
is the map induced by f [Reference Hoyois9, Theorem 3.23]. Our assumptions on codimension imply that
![]() $f^* N_{Z/X} \simeq N_{f^{-1}(Z)/Y}$
, whence
$f^* N_{Z/X} \simeq N_{f^{-1}(Z)/Y}$
, whence
![]() $g \simeq f\rvert _{f^{-1}(Z)} \times \operatorname {id}_{\mathbb A^d}$
. Pullback along
$g \simeq f\rvert _{f^{-1}(Z)} \times \operatorname {id}_{\mathbb A^d}$
. Pullback along
 $Th(g) \simeq \left (f\middle \rvert _{f^{-1}(Z)}\right )_+ \wedge T^d$
thus depends only on
$Th(g) \simeq \left (f\middle \rvert _{f^{-1}(Z)}\right )_+ \wedge T^d$
thus depends only on
![]() $M_{-d}$
, and the result follows.
$M_{-d}$
, and the result follows.
Recall that for (sets, say, and hence presheaves of sets)
![]() $A \subset X, B \subset Y$
, we have a canonical isomorphism
$A \subset X, B \subset Y$
, we have a canonical isomorphism
Construction 3.5. Let
![]() $Z \subset X \times \mathbb P^1$
be closed with image
$Z \subset X \times \mathbb P^1$
be closed with image
![]() $Z'$
in X. Applying the isomorphism (4) with
$Z'$
in X. Applying the isomorphism (4) with
![]() $Y = \mathbb P^1$
,
$Y = \mathbb P^1$
,
![]() $A=X \setminus Z'$
,
$A=X \setminus Z'$
,
![]() $B = \emptyset $
, we obtain the following equivalence:
$B = \emptyset $
, we obtain the following equivalence:
 $$ \begin{align*} X \times \mathbb P^1/\left(X \times \mathbb P^1 \setminus Z' \times \mathbb P^1\right) \simeq (X/X \setminus Z') \wedge \mathbb P^1_+. \end{align*} $$
$$ \begin{align*} X \times \mathbb P^1/\left(X \times \mathbb P^1 \setminus Z' \times \mathbb P^1\right) \simeq (X/X \setminus Z') \wedge \mathbb P^1_+. \end{align*} $$
Together with the stable splitting
![]() and extension of support, this induces a map
and extension of support, this induces a map
 $$ \begin{align*} \mathrm{tr}_Z: H^{d}_{Z}\left(X \times \mathbb P^1, M\right) \to H^{d}_{Z' \times \mathbb P^1}\left(X \times \mathbb P^1, M\right) \to H^{d-1}_{Z'}(X, M_{-1}). \end{align*} $$
$$ \begin{align*} \mathrm{tr}_Z: H^{d}_{Z}\left(X \times \mathbb P^1, M\right) \to H^{d}_{Z' \times \mathbb P^1}\left(X \times \mathbb P^1, M\right) \to H^{d-1}_{Z'}(X, M_{-1}). \end{align*} $$
Remark 3.6. This construction is clearly functorial in X.
Lemma 3.7. In the foregoing notation, suppose that
![]() $Z \subset X \times \mathbb P^1$
has codimension
$Z \subset X \times \mathbb P^1$
has codimension
![]() $\ge d$
(so that
$\ge d$
(so that
![]() $Z' \subset X$
has codimension
$Z' \subset X$
has codimension
![]() $\ge d-1$
). Then
$\ge d-1$
). Then
![]() $\mathrm {tr}_Z$
only depends on
$\mathrm {tr}_Z$
only depends on
![]() $M_{-d}$
.
$M_{-d}$
.
Proof. The transfer is given by pullback along the collapse map
![]() $\mathbb P^1_X/\mathbb P^1_X \setminus \mathbb P^1_{Z'} \to \mathbb P^1_X/\mathbb P^1_X \setminus Z$
. Remarks 3.6 and 3.3 imply that the problem is local on X around generic points of
$\mathbb P^1_X/\mathbb P^1_X \setminus \mathbb P^1_{Z'} \to \mathbb P^1_X/\mathbb P^1_X \setminus Z$
. Remarks 3.6 and 3.3 imply that the problem is local on X around generic points of
![]() $Z'$
of codimension
$Z'$
of codimension
![]() $d-1$
; we may thus assume that
$d-1$
; we may thus assume that
![]() $Z'$
is smooth [22, Tag 0B8X] and
$Z'$
is smooth [22, Tag 0B8X] and
![]() $N_{Z'/X}$
is trivial. Lemma 3.9 identifies the transfer with the collapse map
$N_{Z'/X}$
is trivial. Lemma 3.9 identifies the transfer with the collapse map
 $$ \begin{align*} N_{\mathbb P^1_{Z'}/\mathbb P^1_X}/N_{\mathbb P^1_{Z'}/\mathbb P^1_X} \setminus \mathbb P^1_{Z'} \to N_{\mathbb P^1_{Z'}/\mathbb P^1_X}/N_{\mathbb P^1_{Z'}/\mathbb P^1_X} \setminus Z. \end{align*} $$
$$ \begin{align*} N_{\mathbb P^1_{Z'}/\mathbb P^1_X}/N_{\mathbb P^1_{Z'}/\mathbb P^1_X} \setminus \mathbb P^1_{Z'} \to N_{\mathbb P^1_{Z'}/\mathbb P^1_X}/N_{\mathbb P^1_{Z'}/\mathbb P^1_X} \setminus Z. \end{align*} $$
By assumption,
 $N_{\mathbb P^1_{Z'}/\mathbb P^1_X}$
is trivial of rank
$N_{\mathbb P^1_{Z'}/\mathbb P^1_X}$
is trivial of rank
![]() $d-1$
, so this map identifies with
$d-1$
, so this map identifies with
 $$ \begin{align*} \mathbb A^{d-1}_{\mathbb P^1_{Z'}} / \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus \mathbb P^1_{Z'} \to \mathbb A^{d-1}_{\mathbb P^1_{Z'}} / \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus Z. \end{align*} $$
$$ \begin{align*} \mathbb A^{d-1}_{\mathbb P^1_{Z'}} / \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus \mathbb P^1_{Z'} \to \mathbb A^{d-1}_{\mathbb P^1_{Z'}} / \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus Z. \end{align*} $$
Applying isomorphism (4) with
![]() $X = \mathbb A^{d-1}$
,
$X = \mathbb A^{d-1}$
,
![]() $Y = \mathbb P^1_{Z'}$
,
$Y = \mathbb P^1_{Z'}$
,
![]() $A = \mathbb A^{d-1} \setminus 0$
, and respectively
$A = \mathbb A^{d-1} \setminus 0$
, and respectively
![]() $B=\emptyset $
or
$B=\emptyset $
or
![]() $B=\mathbb P^1_{Z'} \setminus Z$
, this identifies with
$B=\mathbb P^1_{Z'} \setminus Z$
, this identifies with
 $$ \begin{align*} \mathbb A^{d-1}/\mathbb A^{d-1} \setminus 0 \wedge \mathbb P^1_{Z'+} \xrightarrow{\operatorname{id} \wedge t} \mathbb A^{d-1}/\mathbb A^{d-1} \setminus 0 \wedge \mathbb P^1_{Z'}/\mathbb P^1_{Z'} \setminus Z. \end{align*} $$
$$ \begin{align*} \mathbb A^{d-1}/\mathbb A^{d-1} \setminus 0 \wedge \mathbb P^1_{Z'+} \xrightarrow{\operatorname{id} \wedge t} \mathbb A^{d-1}/\mathbb A^{d-1} \setminus 0 \wedge \mathbb P^1_{Z'}/\mathbb P^1_{Z'} \setminus Z. \end{align*} $$
![]() $\Big ($
Use the fact that
$\Big ($
Use the fact that
 $\left (\mathbb A^{d-1} \setminus 0\right ) \times \mathbb P^1_{Z'} = \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus \mathbb P^1_{Z'}$
and
$\left (\mathbb A^{d-1} \setminus 0\right ) \times \mathbb P^1_{Z'} = \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus \mathbb P^1_{Z'}$
and
 $\left (\mathbb A^{d-1} \setminus 0\right ) \times \mathbb P^1_{Z'} \cup \mathbb A^{d-1} \times \left (\mathbb P^1_{Z'} \setminus Z\right ) = \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus Z\Big )$
. Pullback along t is the monogeneic transfer for
$\left (\mathbb A^{d-1} \setminus 0\right ) \times \mathbb P^1_{Z'} \cup \mathbb A^{d-1} \times \left (\mathbb P^1_{Z'} \setminus Z\right ) = \mathbb A^{d-1}_{\mathbb P^1_{Z'}} \setminus Z\Big )$
. Pullback along t is the monogeneic transfer for
![]() $Z/Z'$
, essentially by definition (see §2.1.8). The result follows.
$Z/Z'$
, essentially by definition (see §2.1.8). The result follows.
Remark 3.8. The foregoing proof shows that on the level of the Rost–Schmid complex, the map
![]() $\mathrm {tr}_Z$
is given as follows. For
$\mathrm {tr}_Z$
is given as follows. For
![]() $z \in Z$
of codimension e in
$z \in Z$
of codimension e in
![]() $X \times \mathbb P^1$
and with image
$X \times \mathbb P^1$
and with image
![]() $z'$
of codimension
$z'$
of codimension
![]() $e-1$
in X, the map is given in components by
$e-1$
in X, the map is given in components by
 $$ \begin{align*} & C^e\left(X \times \mathbb P^1, M\right) \supset M_{-e}\left(z, \omega_{z/X \times \mathbb P^1}\right)\\ & \quad \simeq M_{-e}\left(z, \omega_{z/\mathbb P^1_{z'}} \otimes \omega_{\mathbb P^1_{z'}/\mathbb P^1_X}\right) \xrightarrow{\mathrm{tr}} M_{-e}\left(z', \omega_{z'/X}\right) \subset C^{e-1}(X, M_{-1}). \end{align*} $$
$$ \begin{align*} & C^e\left(X \times \mathbb P^1, M\right) \supset M_{-e}\left(z, \omega_{z/X \times \mathbb P^1}\right)\\ & \quad \simeq M_{-e}\left(z, \omega_{z/\mathbb P^1_{z'}} \otimes \omega_{\mathbb P^1_{z'}/\mathbb P^1_X}\right) \xrightarrow{\mathrm{tr}} M_{-e}\left(z', \omega_{z'/X}\right) \subset C^{e-1}(X, M_{-1}). \end{align*} $$
Here
![]() $\mathrm {tr}$
is the monogeneic transfer coming from the embedding
$\mathrm {tr}$
is the monogeneic transfer coming from the embedding
![]() $z \in \mathbb P^1_{z'}$
.
$z \in \mathbb P^1_{z'}$
.
We have used the following form of the homotopy purity equivalence:
Lemma 3.9. Let
![]() $Z \subset Y \subset X$
be closed immersions with
$Z \subset Y \subset X$
be closed immersions with
![]() $X, Y$
smooth. Then the collapse map
$X, Y$
smooth. Then the collapse map
is canonically homotopic to the collapse map
Proof. Write
![]() $X^{\prime } = X \setminus Z$
and
$X^{\prime } = X \setminus Z$
and
![]() $Y' = Y \setminus Z$
. We can write the collapse map as
$Y' = Y \setminus Z$
. We can write the collapse map as
 $$ \begin{align*} \frac{X}{X \setminus Y} \to \frac{X/X \setminus Y}{X^{\prime}/X^{\prime} \setminus Y'}. \end{align*} $$
$$ \begin{align*} \frac{X}{X \setminus Y} \to \frac{X/X \setminus Y}{X^{\prime}/X^{\prime} \setminus Y'}. \end{align*} $$
Since
![]() $(X^{\prime }, Y') \to (X, Y)$
is a morphism of smooth closed pairs, it is compatible with purity equivalences [Reference Hoyois9, after proof of Theorem 3.23], and so the collapse map identifies with
$(X^{\prime }, Y') \to (X, Y)$
is a morphism of smooth closed pairs, it is compatible with purity equivalences [Reference Hoyois9, after proof of Theorem 3.23], and so the collapse map identifies with
 $$ \begin{align*} \frac{N_{Y/X}}{N_{Y/X} \setminus Y} \to \frac{N_{Y/X}/\left(N_{Y/X} \setminus Y\right)}{N_{Y'/X^{\prime}}/\left(N_{Y'/X^{\prime}} \setminus Y'\right)} \simeq \frac{N_{Y/X}}{\left(N_{Y/X} \setminus Y\right) \cup N_{Y'/X^{\prime}}} = \frac{N_{Y/X}}{N_{Y/X} \setminus Z}; \end{align*} $$
$$ \begin{align*} \frac{N_{Y/X}}{N_{Y/X} \setminus Y} \to \frac{N_{Y/X}/\left(N_{Y/X} \setminus Y\right)}{N_{Y'/X^{\prime}}/\left(N_{Y'/X^{\prime}} \setminus Y'\right)} \simeq \frac{N_{Y/X}}{\left(N_{Y/X} \setminus Y\right) \cup N_{Y'/X^{\prime}}} = \frac{N_{Y/X}}{N_{Y/X} \setminus Z}; \end{align*} $$
see also [Reference Hoyois9, top of p. 24]. This is the desired result.
Lemma 3.10. Let X be (essentially) smooth,
![]() $i: Y \hookrightarrow X$
closed of codimension
$i: Y \hookrightarrow X$
closed of codimension
![]() $1$
with Y essentially smooth, and
$1$
with Y essentially smooth, and
![]() $Z \subset X \times \mathbb P^1$
of codimension
$Z \subset X \times \mathbb P^1$
of codimension
![]() $\ge d$
such that
$\ge d$
such that
 $W := \left (Y \times \mathbb P^1\right ) \cap Z$
also has codimension
$W := \left (Y \times \mathbb P^1\right ) \cap Z$
also has codimension
![]() $\ge d$
on
$\ge d$
on
![]() $Y \times \mathbb P^1$
. Write
$Y \times \mathbb P^1$
. Write
![]() $Z', W'$
for the images of Z and W in
$Z', W'$
for the images of Z and W in
![]() $X, Y$
, respectively. Let
$X, Y$
, respectively. Let
![]() $\eta _1, \ldots , \eta _r$
be the generic points of W of codimension d. Suppose further that
$\eta _1, \ldots , \eta _r$
be the generic points of W of codimension d. Suppose further that
![]() $Z \to Z'$
is quasi-finite and
$Z \to Z'$
is quasi-finite and
![]() $W \to W'$
is birational at
$W \to W'$
is birational at
![]() $\eta _1$
. Then
$\eta _1$
. Then
 $$ \begin{align*} i^*: H^d_Z\left(X \times \mathbb P^1, M\right) \to H^d_{W}\left(Y \times \mathbb P^1, M\right) \end{align*} $$
$$ \begin{align*} i^*: H^d_Z\left(X \times \mathbb P^1, M\right) \to H^d_{W}\left(Y \times \mathbb P^1, M\right) \end{align*} $$
depends only on
![]() $M_{-d}$
, the map
$M_{-d}$
, the map
 $$ \begin{align*} i^*: H^{d-1}_{Z'}(X, M_{-1}) \to H^{d-1}_{W'}(Y, M_{-1}), \end{align*} $$
$$ \begin{align*} i^*: H^{d-1}_{Z'}(X, M_{-1}) \to H^{d-1}_{W'}(Y, M_{-1}), \end{align*} $$
and the maps
 $$ \begin{align*} i^*_{\eta_j}: H^d_Z\left(\left(X \times \mathbb P^1\right)_{\eta_j}, M\right) \to H^d_{W}\left(\left(Y \times \mathbb P^1\right)_{\eta_j}, M\right), \end{align*} $$
$$ \begin{align*} i^*_{\eta_j}: H^d_Z\left(\left(X \times \mathbb P^1\right)_{\eta_j}, M\right) \to H^d_{W}\left(\left(Y \times \mathbb P^1\right)_{\eta_j}, M\right), \end{align*} $$
for
![]() $j> 1$
.
$j> 1$
.
In particular, the map
![]() $i^*$
does not depend on
$i^*$
does not depend on
![]() $i_1^*$
.
$i_1^*$
.
Proof. By Remarks 3.6 and 3.8, we have a commutative diagram

By Lemma 3.7, the vertical maps depend only on
![]() $M_{-d}$
, and it follows from Remark 3.8 and our assumption that
$M_{-d}$
, and it follows from Remark 3.8 and our assumption that
![]() $W \to W'$
is birational at
$W \to W'$
is birational at
![]() $\eta _1$
that the right-hand vertical map is injective on the component corresponding to
$\eta _1$
that the right-hand vertical map is injective on the component corresponding to
![]() $\eta _1$
. Set
$\eta _1$
. Set
 $a \in H^d_Z\left (X \times \mathbb P^1, M\right )$
. Write
$a \in H^d_Z\left (X \times \mathbb P^1, M\right )$
. Write
![]() $i^*(a) = b_1 + \cdots + b_r$
, where
$i^*(a) = b_1 + \cdots + b_r$
, where
 $b_i \in C^d_{\eta _i}\left (Y \times \mathbb P^1, M\right )$
. For
$b_i \in C^d_{\eta _i}\left (Y \times \mathbb P^1, M\right )$
. For
![]() $j>1$
, we know
$j>1$
, we know
![]() $i_{\eta _j}^*$
, hence we know
$i_{\eta _j}^*$
, hence we know
![]() $b_j$
and thus we know
$b_j$
and thus we know
![]() $\mathrm {tr}_W\left (b_j\right )$
. Since we know the bottom horizontal map, we know
$\mathrm {tr}_W\left (b_j\right )$
. Since we know the bottom horizontal map, we know
![]() $i^* \mathrm {tr}_Z(a) = \mathrm {tr}_W(i^*(a))$
. Consequently, we know
$i^* \mathrm {tr}_Z(a) = \mathrm {tr}_W(i^*(a))$
. Consequently, we know
 $\mathrm {tr}_W(b_1) = \mathrm {tr}_W(i^*a) - \sum _{j>1} \mathrm {tr}_W\left (b_j\right )$
, and hence
$\mathrm {tr}_W(b_1) = \mathrm {tr}_W(i^*a) - \sum _{j>1} \mathrm {tr}_W\left (b_j\right )$
, and hence
![]() $b_1$
. This concludes the proof.
$b_1$
. This concludes the proof.
Example 3.11. If
![]() $d=1$
, then the map
$d=1$
, then the map
 $i^*: H^{d-1}_{Z'}(X, M_{-1}) \subset M_{-1}(X) \to H^{d-1}_{W'}(Y, M_{-1}) \subset M_{-1}(Y)$
clearly depends only on
$i^*: H^{d-1}_{Z'}(X, M_{-1}) \subset M_{-1}(X) \to H^{d-1}_{W'}(Y, M_{-1}) \subset M_{-1}(Y)$
clearly depends only on
![]() $M_{-1}$
, as desired.
$M_{-1}$
, as desired.
Example 3.12. If Z is smooth and transverse to Y at
![]() $\eta _j$
for
$\eta _j$
for
![]() $j>1$
, then
$j>1$
, then
![]() $i^*_{\eta _j}$
depends only on
$i^*_{\eta _j}$
depends only on
![]() $M_{-d}$
by Lemma 3.4, as desired.
$M_{-d}$
by Lemma 3.4, as desired.
The following is the key reduction. It is an adaptation of [Reference Levine11, Lemma 7.2].
Lemma 3.13. Let
![]() $X, Y$
be (essentially) smooth,
$X, Y$
be (essentially) smooth,
![]() $i: Y \hookrightarrow X$
closed of codimension
$i: Y \hookrightarrow X$
closed of codimension
![]() $1$
, and
$1$
, and
![]() $Z \subset X$
of codimension
$Z \subset X$
of codimension
![]() $\ge d$
such that
$\ge d$
such that
![]() $W = Y \cap Z$
is of codimension
$W = Y \cap Z$
is of codimension
![]() $\ge d$
in Y. Then
$\ge d$
in Y. Then
depends only on
![]() $M_{-d}$
.
$M_{-d}$
.
Proof. By a continuity argument, we may assume that X is smooth over k.
Using Remark 3.3, we may shrink X around a generic point of W. We may thus assume that W is smooth over k and connected. Pullback along the smooth map
![]() $X \times \mathbb A^1 \to X$
yields an understood isomorphism
$X \times \mathbb A^1 \to X$
yields an understood isomorphism
 $H^d_Z(X, M) \to H^d_{Z \times \mathbb A^1}\left (X \times \mathbb A^1, M\right )$
, functorial in X. It hence suffices to understand pullback along
$H^d_Z(X, M) \to H^d_{Z \times \mathbb A^1}\left (X \times \mathbb A^1, M\right )$
, functorial in X. It hence suffices to understand pullback along
![]() $i \times \mathbb A^1$
. Let
$i \times \mathbb A^1$
. Let
![]() $w=\mathrm {Spec}(F)$
be a generic point of
$w=\mathrm {Spec}(F)$
be a generic point of
![]() $W \times \mathbb A^1$
of codimension d on
$W \times \mathbb A^1$
of codimension d on
![]() $Y \times \mathbb A^1$
. Then w lies over the generic point of
$Y \times \mathbb A^1$
. Then w lies over the generic point of
![]() $\mathbb A^1$
[22, Tag 0CC1]. We may thus (using Remark 3.3 again) pass to the generic fiber over
$\mathbb A^1$
[22, Tag 0CC1]. We may thus (using Remark 3.3 again) pass to the generic fiber over
![]() $\mathrm {Spec}(k(t)) \in \mathbb A^1$
; essentially we have base-changed the entire problem to
$\mathrm {Spec}(k(t)) \in \mathbb A^1$
; essentially we have base-changed the entire problem to
![]() $k(t)/k$
. Let us denote the base change of X by
$k(t)/k$
. Let us denote the base change of X by
![]() $X_1$
, and so on. Since Z is geometrically reduced over k [22, Tag 020I], its base change
$X_1$
, and so on. Since Z is geometrically reduced over k [22, Tag 020I], its base change
![]() $Z_1$
is geometrically reduced over
$Z_1$
is geometrically reduced over
![]() $k(t)$
[22, Tag 0384]. Lemma 3.14 below supplies us with an étale neighborhood
$k(t)$
[22, Tag 0384]. Lemma 3.14 below supplies us with an étale neighborhood
![]() $X_2 \to X_1$
of w and a smooth map
$X_2 \to X_1$
of w and a smooth map
![]() $X_2 \to W_1$
such that
$X_2 \to W_1$
such that
![]() $Z_2 \to X_2 \to W_1$
is generically smooth and
$Z_2 \to X_2 \to W_1$
is generically smooth and
![]() $Y_2 \to W_1$
is smooth. Let
$Y_2 \to W_1$
is smooth. Let
![]() $X_3 = X_2 \times _{W_1} \{w\}$
. Our base changes are illustrated in the following diagram:
$X_3 = X_2 \times _{W_1} \{w\}$
. Our base changes are illustrated in the following diagram:

By construction,
![]() $X_3 \to X_1$
is a pro-(étale neighborhood) of
$X_3 \to X_1$
is a pro-(étale neighborhood) of
![]() $w \in X \otimes k(t)$
, and so (again using Remark 3.3) we may replace
$w \in X \otimes k(t)$
, and so (again using Remark 3.3) we may replace
![]() $X \otimes k(t)$
by
$X \otimes k(t)$
by
![]() $X_3$
.
$X_3$
.
With these preparatory constructions out of the way, we rename
![]() $X_3$
to X,
$X_3$
to X,
![]() $Y_3$
to Y, and
$Y_3$
to Y, and
![]() $Z_3$
to Z. We now have a smooth map
$Z_3$
to Z. We now have a smooth map
![]() $X \to \mathrm {Spec}(F)$
, where F is infinite (since it contains
$X \to \mathrm {Spec}(F)$
, where F is infinite (since it contains
![]() $k(t)$
),
$k(t)$
),
![]() $Y \to \mathrm {Spec}(F)$
is smooth, and
$Y \to \mathrm {Spec}(F)$
is smooth, and
![]() $Z \to \mathrm {Spec}(F)$
is generically smooth. Also,
$Z \to \mathrm {Spec}(F)$
is generically smooth. Also,
![]() $W = \{w\}$
is an F-rational point of X,
$W = \{w\}$
is an F-rational point of X,
![]() $\dim X = d+1$
,
$\dim X = d+1$
,
![]() $\dim Y = d$
, and
$\dim Y = d$
, and
![]() $\dim Z = 1$
. Shrinking X if necessary, we may assume that
$\dim Z = 1$
. Shrinking X if necessary, we may assume that
![]() $Y \subset X$
is principal, say cut out by
$Y \subset X$
is principal, say cut out by
![]() $f \in \mathcal O(X)$
, that every component of Z meets w, that Z is smooth away from w, and that X is affine.
$f \in \mathcal O(X)$
, that every component of Z meets w, that Z is smooth away from w, and that X is affine.
Lemma 3.16 supplies us with
![]() $\bar u: Z \to \mathbb A^1$
with
$\bar u: Z \to \mathbb A^1$
with
![]() $\bar u(w) \ne 0$
,
$\bar u(w) \ne 0$
,
![]() $\bar u f: Z \to \mathbb A^1$
finite, and
$\bar u f: Z \to \mathbb A^1$
finite, and
![]() $\bar u$
having no double roots. Pick
$\bar u$
having no double roots. Pick
![]() $u \in \mathcal O(X)$
reducing to
$u \in \mathcal O(X)$
reducing to
![]() $\bar u \in \mathcal O(Z)$
. Then
$\bar u \in \mathcal O(Z)$
. Then
![]() $\phi _1 := uf: X \to \mathbb A^1$
is finite when restricted to Z and satisfies
$\phi _1 := uf: X \to \mathbb A^1$
is finite when restricted to Z and satisfies
![]() $\phi _1(w) = 0$
, and we claim that
$\phi _1(w) = 0$
, and we claim that
![]() $\phi _1$
is smooth at all points of
$\phi _1$
is smooth at all points of
![]() $\phi _1^{-1}(0) \cap Z$
. Note that by construction,
$\phi _1^{-1}(0) \cap Z$
. Note that by construction,
![]() $(u,f)$
have no common root on Z (w being the only root of f on Z), and neither do
$(u,f)$
have no common root on Z (w being the only root of f on Z), and neither do
![]() $(u,du)$
(u not having double roots on Z) or
$(u,du)$
(u not having double roots on Z) or
![]() $(f, df)$
(
$(f, df)$
(
![]() $Z(f)$
being smooth). It follows that
$Z(f)$
being smooth). It follows that
![]() $d(uf) = udf + fdu$
does not vanish at points
$d(uf) = udf + fdu$
does not vanish at points
![]() $p \in Z$
with
$p \in Z$
with
![]() $(uf)(p) = 0$
, proving the claim.
$(uf)(p) = 0$
, proving the claim.
We may thus apply Lemma 3.17 to obtain
![]() $\phi _2, \ldots , \phi _{d+1}: X \to \mathbb A^1$
such that
$\phi _2, \ldots , \phi _{d+1}: X \to \mathbb A^1$
such that
![]() $\phi = (\phi _1, \ldots , \phi _{d+1}): X \to \mathbb A^{d+1}$
is étale at all points of
$\phi = (\phi _1, \ldots , \phi _{d+1}): X \to \mathbb A^{d+1}$
is étale at all points of
![]() $\phi _1^{-1}(0) \cap Z$
and has
$\phi _1^{-1}(0) \cap Z$
and has
![]() $\phi (w) = 0$
, and there exists an open neighborhood
$\phi (w) = 0$
, and there exists an open neighborhood
![]() $0 \in U \subset \mathbb A^{d}_F$
such that
$0 \in U \subset \mathbb A^{d}_F$
such that
 $Z_U \xrightarrow {\phi } \mathbb A^1_U$
is a closed immersion (in fact,
$Z_U \xrightarrow {\phi } \mathbb A^1_U$
is a closed immersion (in fact,
![]() $U=U_1 \times \mathbb A^{d-1}$
). The non-étale locus of
$U=U_1 \times \mathbb A^{d-1}$
). The non-étale locus of
![]() $\phi $
meets Z in finitely many points (namely a closed subset not containing w, and hence no component of the curve Z), none of which map to
$\phi $
meets Z in finitely many points (namely a closed subset not containing w, and hence no component of the curve Z), none of which map to
![]() $0$
under
$0$
under
![]() $\phi _1$
. Shrinking U further, we may thus assume that
$\phi _1$
. Shrinking U further, we may thus assume that
![]() $Z_U$
is contained in the étale locus V of
$Z_U$
is contained in the étale locus V of
![]() $\phi $
. Since
$\phi $
. Since
![]() $Z_U \simeq \phi (Z_U) \to \phi ^{-1}(\phi (Z_U)) \cap V$
is a section of a separated unramified morphism, it is clopen [22, Tag 024T] – that is, we have
$Z_U \simeq \phi (Z_U) \to \phi ^{-1}(\phi (Z_U)) \cap V$
is a section of a separated unramified morphism, it is clopen [22, Tag 024T] – that is, we have
![]() $\phi ^{-1}(\phi (Z_U)) \cap V = Z_U \coprod Z'$
with
$\phi ^{-1}(\phi (Z_U)) \cap V = Z_U \coprod Z'$
with
![]() $Z'$
closed in V.
$Z'$
closed in V.
Let
![]() $D = D(u)$
; this is an open neighborhood of w in X. Note that
$D = D(u)$
; this is an open neighborhood of w in X. Note that
![]() $Z(uf) \cap D = Y \cap D$
. Let
$Z(uf) \cap D = Y \cap D$
. Let
 $$ \begin{gather*} X^{\prime} = \left(\phi^{-1}\left(\mathbb A^1_U\right) \cap V\right) \setminus Z', \\ U_0 = U \cap \left(\{0\} \times \mathbb A^{d-1}\right), \text{ and } Y' = \phi^{-1}\left(\mathbb A^1_{U_0}\right) \cap X^{\prime} = Z(uf) \cap X^{\prime}. \end{gather*} $$
$$ \begin{gather*} X^{\prime} = \left(\phi^{-1}\left(\mathbb A^1_U\right) \cap V\right) \setminus Z', \\ U_0 = U \cap \left(\{0\} \times \mathbb A^{d-1}\right), \text{ and } Y' = \phi^{-1}\left(\mathbb A^1_{U_0}\right) \cap X^{\prime} = Z(uf) \cap X^{\prime}. \end{gather*} $$
We have a commutative diagram of schemes

Here j is the canonical closed immersion and
![]() $\psi $
is the restriction (i.e., base change) of
$\psi $
is the restriction (i.e., base change) of
![]() $\phi $
. In particular,
$\phi $
. In particular,
![]() $\psi $
is étale and
$\psi $
is étale and
![]() $Y'$
is smooth. By construction,
$Y'$
is smooth. By construction,
![]() $\phi $
is an étale neighborhood of
$\phi $
is an étale neighborhood of
![]() $Z_U$
, and
$Z_U$
, and
 $Z_U \xrightarrow {\phi } \mathbb A^1_U \to U$
is finite. There is an induced commutative diagram
$Z_U \xrightarrow {\phi } \mathbb A^1_U \to U$
is finite. There is an induced commutative diagram

We need to understand the top left-hand horizontal map. All the labeled isomorphisms are pullback along étale maps, and isomorphisms by excision. The two maps labeled o are also pullback along étale morphisms (in fact open immersions), and hence understood.
We have thus reduced to understanding
![]() $j^*$
; we rename
$j^*$
; we rename
![]() $Z_U$
to Z and
$Z_U$
to Z and
![]() $Z_U \cap Z(uf)$
to V. Since Z is finite over U, it remains closed in
$Z_U \cap Z(uf)$
to V. Since Z is finite over U, it remains closed in
![]() $\mathbb P^1_U$
, and hence by a further excision argument it suffices to understand
$\mathbb P^1_U$
, and hence by a further excision argument it suffices to understand
 $$ \begin{align*} \bar j^*: H^d_Z\left(\mathbb P^1_U, M\right) \to H^d_V\left(\mathbb P^1_{U_0}, M\right). \end{align*} $$
$$ \begin{align*} \bar j^*: H^d_Z\left(\mathbb P^1_U, M\right) \to H^d_V\left(\mathbb P^1_{U_0}, M\right). \end{align*} $$
We have
![]() $V = \{w, z_1, \ldots , z_r\}$
, and each
$V = \{w, z_1, \ldots , z_r\}$
, and each
![]() $z_i$
is a smooth point of Z (since w is the only singular point of Z). Moreover,
$z_i$
is a smooth point of Z (since w is the only singular point of Z). Moreover,
![]() $z_i$
is a smooth point of V, since
$z_i$
is a smooth point of V, since
![]() $z_i$
is a simple root of u (since by construction u has no double roots on Z). By Lemma 3.4, the pullback
$z_i$
is a simple root of u (since by construction u has no double roots on Z). By Lemma 3.4, the pullback
 $$ \begin{align*} j_s^*: H^d_Z\left(\left(\mathbb P^1_U\right)_{z_s}, M\right) \to H^d_V\left(\left(\mathbb P^1_{U_0}\right)_{z_s}, M\right) \end{align*} $$
$$ \begin{align*} j_s^*: H^d_Z\left(\left(\mathbb P^1_U\right)_{z_s}, M\right) \to H^d_V\left(\left(\mathbb P^1_{U_0}\right)_{z_s}, M\right) \end{align*} $$
depends only on
![]() $M_{-d}$
. Thus applying Lemma 3.10, it suffices to understand
$M_{-d}$
. Thus applying Lemma 3.10, it suffices to understand
 $$ \begin{align*} k^*: H^{d-1}_{Z'}(U, M_{-1}) \to H^{d-1}_{V^{\prime}}(U_0, M_{-1}); \end{align*} $$
$$ \begin{align*} k^*: H^{d-1}_{Z'}(U, M_{-1}) \to H^{d-1}_{V^{\prime}}(U_0, M_{-1}); \end{align*} $$
here
![]() $Z'$
and
$Z'$
and
![]() $V^{\prime }$
are the images of Z and V in U. If
$V^{\prime }$
are the images of Z and V in U. If
![]() $d=1$
, we are done, by Example 3.11. The general case (i.e.,
$d=1$
, we are done, by Example 3.11. The general case (i.e.,
![]() $d>1$
) now follows by induction (i.e., restart the argument with
$d>1$
) now follows by induction (i.e., restart the argument with
![]() $(U, U_0, Z')$
in place of
$(U, U_0, Z')$
in place of
![]() $(X,Y,Z)$
).
$(X,Y,Z)$
).
Lemma 3.14. Let X be a smooth scheme over an infinite field K,
![]() $W \subset X, Y \subset X$
smooth closed subschemes,
$W \subset X, Y \subset X$
smooth closed subschemes,
![]() $W \subset Z \subset X$
with
$W \subset Z \subset X$
with
![]() $Z \subset X$
closed, and Z geometrically reduced over K (but not necessarily smooth). Set
$Z \subset X$
closed, and Z geometrically reduced over K (but not necessarily smooth). Set
![]() $w \in W \cap Y$
such that
$w \in W \cap Y$
such that
![]() $\dim _w W \le \dim _w Y$
. There exists an étale neighborhood
$\dim _w W \le \dim _w Y$
. There exists an étale neighborhood
![]() $X^{\prime } \to X$
of w together with a smooth morphism
$X^{\prime } \to X$
of w together with a smooth morphism
![]() $X^{\prime } \to W$
such that
$X^{\prime } \to W$
such that
![]() $Z \times _X X^{\prime } \to W$
is generically smooth (that is, the smooth locus is dense in the source) and
$Z \times _X X^{\prime } \to W$
is generically smooth (that is, the smooth locus is dense in the source) and
![]() $Y \times _X X^{\prime } \to W$
is smooth.
$Y \times _X X^{\prime } \to W$
is smooth.
Proof. We modify [Reference Déglise4, Corollary 5.11]. Shrinking X around w, we may assume that X is affine and there exist
![]() $f_1, \ldots , f_d \in \mathcal O(X)$
such that
$f_1, \ldots , f_d \in \mathcal O(X)$
such that
![]() $W = Z(f_1, \ldots , f_d)$
and W has codimension everywhere exactly d in X. Let
$W = Z(f_1, \ldots , f_d)$
and W has codimension everywhere exactly d in X. Let
![]() $\{z_1, \ldots , z_r\} \subset Z$
be a choice of smooth points in every component of Z, which exist because Z is geometrically reduced [22, Tag 056V]. Let
$\{z_1, \ldots , z_r\} \subset Z$
be a choice of smooth points in every component of Z, which exist because Z is geometrically reduced [22, Tag 056V]. Let
![]() $\dim X = d+n$
. We claim that there exist
$\dim X = d+n$
. We claim that there exist
![]() $g_1, \ldots , g_n \in \mathcal O(X)$
such that
$g_1, \ldots , g_n \in \mathcal O(X)$
such that
![]() $dg_1, \ldots , dg_n$
are linearly independent (over the respective residue fields) in
$dg_1, \ldots , dg_n$
are linearly independent (over the respective residue fields) in
![]() $\Omega _w W$
,
$\Omega _w W$
,
![]() $\Omega _w Y$
, and
$\Omega _w Y$
, and
![]() $\Omega _{z_i} Z$
for every i; we shall prove this at the end. It follows that
$\Omega _{z_i} Z$
for every i; we shall prove this at the end. It follows that
![]() $df_1, \ldots , df_d$
and
$df_1, \ldots , df_d$
and
![]() $dg_1, \ldots , dg_n$
are linearly independent in
$dg_1, \ldots , dg_n$
are linearly independent in
![]() $\Omega _w X$
. Consider the map
$\Omega _w X$
. Consider the map
![]() $F = (f_1, \ldots , f_d, g_1, \ldots , g_n): X \to \mathbb A^{d+n}$
. Let
$F = (f_1, \ldots , f_d, g_1, \ldots , g_n): X \to \mathbb A^{d+n}$
. Let
![]() $p: \mathbb A^{d+n} \to \mathbb A^n$
be the projection to the last n coordinates. By [Reference Grothendieck8, 17.11.1], F is smooth at w,
$p: \mathbb A^{d+n} \to \mathbb A^n$
be the projection to the last n coordinates. By [Reference Grothendieck8, 17.11.1], F is smooth at w,
![]() $pF\rvert _W$
is smooth at w,
$pF\rvert _W$
is smooth at w,
![]() $pF\rvert _Y$
is smooth at w, and
$pF\rvert _Y$
is smooth at w, and
![]() $pF\rvert _Z$
is smooth at
$pF\rvert _Z$
is smooth at
![]() $z_i$
. In particular,
$z_i$
. In particular,
![]() $pF\rvert _Z$
is generically smooth. Shrinking X further around w, we may assume that F,
$pF\rvert _Z$
is generically smooth. Shrinking X further around w, we may assume that F,
![]() $pF\rvert _W$
, and
$pF\rvert _W$
, and
![]() $pF\rvert _Y$
are smooth (whence the former two are étale), and of course
$pF\rvert _Y$
are smooth (whence the former two are étale), and of course
![]() $pF\rvert _Z$
remains generically smooth. Applying the construction of [Reference Déglise4, §5.5, §5.9], we obtain a commutative diagram as follows:
$pF\rvert _Z$
remains generically smooth. Applying the construction of [Reference Déglise4, §5.5, §5.9], we obtain a commutative diagram as follows:

Here both squares are cartesian by definition, j is an open immersion, and
![]() $qj$
is an étale neighborhood of W (by construction of
$qj$
is an étale neighborhood of W (by construction of
![]() $\Omega $
). Since p, F, and j are smooth, so is
$\Omega $
). Since p, F, and j are smooth, so is
![]() $\Omega \to W$
. By construction,
$\Omega \to W$
. By construction,
![]() $Z \to X \to \mathbb A^n$
is generically smooth, thus so is
$Z \to X \to \mathbb A^n$
is generically smooth, thus so is
![]() $Z \times _X P \to W$
, and hence also
$Z \times _X P \to W$
, and hence also
![]() $Z \times _X \Omega \to W$
. Similarly,
$Z \times _X \Omega \to W$
. Similarly,
![]() $Y \to X \to \mathbb A^n$
is smooth and hence so is
$Y \to X \to \mathbb A^n$
is smooth and hence so is
![]() $Y \times _X \Omega \to W$
. Setting
$Y \times _X \Omega \to W$
. Setting
![]() $X^{\prime } = \Omega $
, the result follows.
$X^{\prime } = \Omega $
, the result follows.
It remains to prove the claim. Embed X into
![]() $\mathbb A^N$
, and let
$\mathbb A^N$
, and let
![]() $g_1, \ldots , g_n$
be linear projections. By Lemma 3.15 applied to
$g_1, \ldots , g_n$
be linear projections. By Lemma 3.15 applied to
 $\left (\mathbb A^N\right )^* \otimes _K K(w) \subset \left (\Omega \mathbb A^N\right ) \otimes _K K(w) \rightarrow \Omega _w W$
,
$\left (\mathbb A^N\right )^* \otimes _K K(w) \subset \left (\Omega \mathbb A^N\right ) \otimes _K K(w) \rightarrow \Omega _w W$
,
![]() $dg_1, \ldots , dg_n$
will be linearly independent in
$dg_1, \ldots , dg_n$
will be linearly independent in
![]() $\Omega _w W$
for general
$\Omega _w W$
for general
![]() $g_j$
, and similarly for
$g_j$
, and similarly for
![]() $\Omega _w Y$
and
$\Omega _w Y$
and
![]() $\Omega _{z_i} Z$
. The result follows.
$\Omega _{z_i} Z$
. The result follows.
For completeness, we include a proof of the following elementary fact:
Lemma 3.15. Let
![]() $K^{\prime }/K$
be a finite field extension. Let V be a finite-dimensional K-vector space,
$K^{\prime }/K$
be a finite field extension. Let V be a finite-dimensional K-vector space,
![]() $V^{\prime }$
a
$V^{\prime }$
a
![]() $K^{\prime }$
-vector space of dimension
$K^{\prime }$
-vector space of dimension
![]() $\ge n$
, and
$\ge n$
, and
![]() $V_{K^{\prime }} \to V^{\prime }$
a surjection. Write
$V_{K^{\prime }} \to V^{\prime }$
a surjection. Write
![]() $\mathbb A(V)$
for the associated variety over K (isomorphic to
$\mathbb A(V)$
for the associated variety over K (isomorphic to
![]() $\mathbb A^{\dim V}_K$
). There is a nonempty open subset U of
$\mathbb A^{\dim V}_K$
). There is a nonempty open subset U of
![]() $\mathbb A(V)^n$
such that any
$\mathbb A(V)^n$
such that any
![]() $(v_1, \ldots , v_n) \in U(K)$
have
$(v_1, \ldots , v_n) \in U(K)$
have
![]() $K^{\prime }$
-linearly independent images in
$K^{\prime }$
-linearly independent images in
![]() $V^{\prime }$
. In particular, if F is infinite, then n general elements of V are linearly independent in
$V^{\prime }$
. In particular, if F is infinite, then n general elements of V are linearly independent in
![]() $V^{\prime }$
.
$V^{\prime }$
.
Proof. Replacing
![]() $V^{\prime }$
by a quotient of dimension n, we may assume that
$V^{\prime }$
by a quotient of dimension n, we may assume that
![]() $\dim _{K^{\prime }} V^{\prime } = n$
. There is a map
$\dim _{K^{\prime }} V^{\prime } = n$
. There is a map
![]() $D: \mathbb A(V^{\prime })^n \to \mathbb A_{K^{\prime }}^1$
such that n elements of
$D: \mathbb A(V^{\prime })^n \to \mathbb A_{K^{\prime }}^1$
such that n elements of
![]() $V^{\prime }$
are linearly independent if and only if their image under D is nonzero (pick a basis of
$V^{\prime }$
are linearly independent if and only if their image under D is nonzero (pick a basis of
![]() $V^{\prime }$
and let D be the determinant). By adjunction, the composite
$V^{\prime }$
and let D be the determinant). By adjunction, the composite
 $$ \begin{align*} \mathbb A(V)^n_{K^{\prime}} \to \mathbb A(V^{\prime})^n \xrightarrow{D} \mathbb A^1_{K^{\prime}} \end{align*} $$
$$ \begin{align*} \mathbb A(V)^n_{K^{\prime}} \to \mathbb A(V^{\prime})^n \xrightarrow{D} \mathbb A^1_{K^{\prime}} \end{align*} $$
defines a map
 $D^{\prime }: \mathbb A(V)^n \to R\left (\mathbb A^1_{K^{\prime }}\right )$
, where R denotes the Weil restriction along
$D^{\prime }: \mathbb A(V)^n \to R\left (\mathbb A^1_{K^{\prime }}\right )$
, where R denotes the Weil restriction along
![]() $K^{\prime }/K$
(see, e.g., [Reference Bachmann and Yakerson1, §7.6]). By construction, n elements of V have image in
$K^{\prime }/K$
(see, e.g., [Reference Bachmann and Yakerson1, §7.6]). By construction, n elements of V have image in
![]() $V^{\prime }$
linearly independent over
$V^{\prime }$
linearly independent over
![]() $K^{\prime }$
if and only if their image under
$K^{\prime }$
if and only if their image under
![]() $D^{\prime }$
is nonzero. Since D is not the zero map, neither is
$D^{\prime }$
is nonzero. Since D is not the zero map, neither is
![]() $D^{\prime }$
, and hence
$D^{\prime }$
, and hence
 $U = D^{\prime -1}\left (R\left (\mathbb A^1_{K^{\prime }}\right ) \setminus 0\right )$
is the desired nonempty open subset.
$U = D^{\prime -1}\left (R\left (\mathbb A^1_{K^{\prime }}\right ) \setminus 0\right )$
is the desired nonempty open subset.
The last statement follows because nonempty open subsets of affine space over an infinite field have rational points.
Lemma 3.16. Let Z be an affine curve over the field F, smooth away from a rational point w, and let
![]() $f: Z \to \mathbb A^1$
be nowhere constant. There exists
$f: Z \to \mathbb A^1$
be nowhere constant. There exists
![]() $u: Z \to \mathbb A^1$
such that
$u: Z \to \mathbb A^1$
such that
![]() $u(w) \ne 0$
and
$u(w) \ne 0$
and
![]() $fu: Z \to \mathbb A^1$
is finite. If F is infinite, it can be arranged that u has no double zeros.
$fu: Z \to \mathbb A^1$
is finite. If F is infinite, it can be arranged that u has no double zeros.
Proof. Let
![]() $\bar Z$
be a compactification of Z which is smooth away from w, and
$\bar Z$
be a compactification of Z which is smooth away from w, and
![]() $\bar Z \setminus Z = \{z_1, \ldots , z_r\}$
. Since Z is smooth at infinity, any map
$\bar Z \setminus Z = \{z_1, \ldots , z_r\}$
. Since Z is smooth at infinity, any map
![]() $Z \to \mathbb A^1$
extends to
$Z \to \mathbb A^1$
extends to
![]() $\bar Z \to \mathbb P^1$
. It suffices to find
$\bar Z \to \mathbb P^1$
. It suffices to find
![]() $u_i: Z \to \mathbb A^1$
such that
$u_i: Z \to \mathbb A^1$
such that
![]() $\mathrm {ord}_{z_i}(u_i) + \mathrm {ord}_{z_i}(f) < 0$
, for every i. Then
$\mathrm {ord}_{z_i}(u_i) + \mathrm {ord}_{z_i}(f) < 0$
, for every i. Then
![]() $u = \sum _i u_i^{e_i}$
for suitably big
$u = \sum _i u_i^{e_i}$
for suitably big
![]() $e_i$
will satisfy the same condition, but for all i at once. Now
$e_i$
will satisfy the same condition, but for all i at once. Now
![]() $uf: \bar Z \to \mathbb P^1$
is proper and
$uf: \bar Z \to \mathbb P^1$
is proper and
![]() $\bar Z \setminus Z \supset (uf)^{-1}(\infty ) \supset \{z_1, \ldots , z_r\}$
, which implies that
$\bar Z \setminus Z \supset (uf)^{-1}(\infty ) \supset \{z_1, \ldots , z_r\}$
, which implies that
![]() $uf: Z \to \mathbb A^1$
is finite (being proper and affine). If
$uf: Z \to \mathbb A^1$
is finite (being proper and affine). If
![]() $u(w) = 0$
, then replace u by
$u(w) = 0$
, then replace u by
![]() $u+1$
; the first claim follows. Replacing u by
$u+1$
; the first claim follows. Replacing u by
![]() $u^n + g$
for suitable g and n large, we may assume that
$u^n + g$
for suitable g and n large, we may assume that
![]() $du$
has only finitely many zeros. Then
$du$
has only finitely many zeros. Then
![]() $u+c$
for general c has no double zeros (away from w) and satisfies
$u+c$
for general c has no double zeros (away from w) and satisfies
![]() $u(w) \ne 0$
, so that if F is infinite we may arrange the second claim.
$u(w) \ne 0$
, so that if F is infinite we may arrange the second claim.
Let
![]() $\tilde {\bar Z}$
be the normalization of
$\tilde {\bar Z}$
be the normalization of
![]() $\bar Z$
, and
$\bar Z$
, and
![]() $\tilde Z \subset \tilde {\bar Z}$
the open subset over Z – that is, the normalization of Z. Note that
$\tilde Z \subset \tilde {\bar Z}$
the open subset over Z – that is, the normalization of Z. Note that
![]() $\tilde {\bar Z} \to \bar Z$
is an isomorphism near
$\tilde {\bar Z} \to \bar Z$
is an isomorphism near
![]() $z_i$
. By Riemann–Roch, we can find
$z_i$
. By Riemann–Roch, we can find
![]() $v: \tilde {\bar Z} \to \mathbb P^1$
with an arbitrarily large pole at
$v: \tilde {\bar Z} \to \mathbb P^1$
with an arbitrarily large pole at
![]() $z_i$
and no poles away from
$z_i$
and no poles away from
![]() $z_i$
, so in particular no poles on
$z_i$
, so in particular no poles on
![]() $\tilde Z$
. Since
$\tilde Z$
. Since
![]() $\tilde Z \to Z$
is integral, there exists an equation
$\tilde Z \to Z$
is integral, there exists an equation
![]() $v^n + a_1 v^{n-1} + \cdots + a_n = 0$
, with
$v^n + a_1 v^{n-1} + \cdots + a_n = 0$
, with
![]() $a_i: Z \to \mathbb A^1$
. It follows that (at least) one of the
$a_i: Z \to \mathbb A^1$
. It follows that (at least) one of the
![]() $a_i$
must have a pole at
$a_i$
must have a pole at
![]() $z_i$
(at least) as large as v. This concludes the proof.
$z_i$
(at least) as large as v. This concludes the proof.
We have used the following variant of the second part of Gabber’s lemma [Reference Gabber6, Lemma 3.1(b)]; our proof is heavily inspired by Gabber’s:
Lemma 3.17. Let F be an infinite field, X smooth and affine of dimension d over F,
![]() $Z \subset X$
closed,
$Z \subset X$
closed,
![]() $w \in Z$
a rational point,
$w \in Z$
a rational point,
![]() $e<d$
, and
$e<d$
, and
![]() $\phi ^{\prime } = (\phi _1, \ldots , \phi _e): X \to \mathbb A^e$
such that
$\phi ^{\prime } = (\phi _1, \ldots , \phi _e): X \to \mathbb A^e$
such that
![]() $\phi ^{\prime }(w) = 0$
,
$\phi ^{\prime }(w) = 0$
,
![]() $\phi ^{\prime }\rvert _Z: Z \to \mathbb A^e$
is finite, and
$\phi ^{\prime }\rvert _Z: Z \to \mathbb A^e$
is finite, and
![]() $\phi ^{\prime }$
is smooth at all points of
$\phi ^{\prime }$
is smooth at all points of
![]() $\phi ^{\prime -1}(0) \cap Z$
.
$\phi ^{\prime -1}(0) \cap Z$
.
Then there exist
![]() $\phi _{e+1}, \ldots , \phi _d: X \to \mathbb A^1$
such that
$\phi _{e+1}, \ldots , \phi _d: X \to \mathbb A^1$
such that
![]() $\phi = (\phi _1, \ldots , \phi _d): X \to \mathbb A^d$
is étale at all points of
$\phi = (\phi _1, \ldots , \phi _d): X \to \mathbb A^d$
is étale at all points of
![]() $\phi ^{\prime -1}(0) \cap Z$
,
$\phi ^{\prime -1}(0) \cap Z$
,
![]() $\phi (w) = 0$
, and there exists an open neighborhood
$\phi (w) = 0$
, and there exists an open neighborhood
![]() $0 \in W \subset \mathbb A^{e}$
such that
$0 \in W \subset \mathbb A^{e}$
such that
 $Z_W \to \mathbb A^{d-e}_W$
is a closed immersion.
$Z_W \to \mathbb A^{d-e}_W$
is a closed immersion.
Note that the new map
![]() $\phi $
is also finite when restricted to Z.
$\phi $
is also finite when restricted to Z.
Proof. Set
![]() $X \hookrightarrow \mathbb A^N$
with w mapped to
$X \hookrightarrow \mathbb A^N$
with w mapped to
![]() $0$
. We claim that general linear projections
$0$
. We claim that general linear projections
![]() $\phi _{e+1}, \ldots , \phi _d$
have the desired properties. They vanish on w by definition.
$\phi _{e+1}, \ldots , \phi _d$
have the desired properties. They vanish on w by definition.
In order for
![]() $\phi $
to be smooth at some point
$\phi $
to be smooth at some point
![]() $x \in \phi ^{\prime -1}(0) \cap Z$
, we need only ensure that
$x \in \phi ^{\prime -1}(0) \cap Z$
, we need only ensure that
![]() $d\phi _1, \ldots , d\phi _d \in \Omega _x X$
are linearly independent [Reference Grothendieck8, 17.11.1]. Since
$d\phi _1, \ldots , d\phi _d \in \Omega _x X$
are linearly independent [Reference Grothendieck8, 17.11.1]. Since
![]() $\phi ^{\prime }$
is smooth at x, the
$\phi ^{\prime }$
is smooth at x, the
![]() $d\phi _1, \ldots , d\phi _e$
are linearly independent at x, and then the other
$d\phi _1, \ldots , d\phi _e$
are linearly independent at x, and then the other
![]() $d\phi _i$
are linearly independent, for general
$d\phi _i$
are linearly independent, for general
![]() $\phi _i$
; this follows from Lemma 3.15 applied to
$\phi _i$
; this follows from Lemma 3.15 applied to
![]() $V^{\prime } = \Omega _x X/\left \langle d\phi _1, \ldots , d\phi _e \right \rangle $
. Since
$V^{\prime } = \Omega _x X/\left \langle d\phi _1, \ldots , d\phi _e \right \rangle $
. Since
![]() $\phi ^{\prime -1}(0) \cap Z$
is a finite set of points, the étaleness claim holds for general
$\phi ^{\prime -1}(0) \cap Z$
is a finite set of points, the étaleness claim holds for general
![]() $\phi _i$
.
$\phi _i$
.
It remains to prove the claim about the closed immersion. Note that by Nakayama’s lemma, if
![]() $f: X \to Y$
is a morphism of affine S-schemes with X finite over S and S Noetherian, and there exists
$f: X \to Y$
is a morphism of affine S-schemes with X finite over S and S Noetherian, and there exists
![]() $s \in S$
such that
$s \in S$
such that
![]() $f_s: X_s \to Y_s$
is a closed immersion, then there exists an open neighborhood U of s such that
$f_s: X_s \to Y_s$
is a closed immersion, then there exists an open neighborhood U of s such that
![]() $f_U: X_U \to Y_U$
is a closed immersion. Let
$f_U: X_U \to Y_U$
is a closed immersion. Let
![]() $\psi : Z \to \mathbb A^d$
be the restriction of
$\psi : Z \to \mathbb A^d$
be the restriction of
![]() $\phi $
, which we view as a morphism over
$\phi $
, which we view as a morphism over
![]() $S=\mathbb A^e$
via
$S=\mathbb A^e$
via
![]() $\phi ^{\prime }$
(and the projection
$\phi ^{\prime }$
(and the projection
![]() $\mathbb A^d \to \mathbb A^e$
to the first e coordinates). It is thus enough to show that
$\mathbb A^d \to \mathbb A^e$
to the first e coordinates). It is thus enough to show that
![]() $\psi _0: \phi ^{\prime -1}(0) \cap Z \to \mathbb A^{d-e}$
is a closed immersion (for general
$\psi _0: \phi ^{\prime -1}(0) \cap Z \to \mathbb A^{d-e}$
is a closed immersion (for general
![]() $\phi _i$
). Since
$\phi _i$
). Since
![]() $\phi $
is étale at all points of
$\phi $
is étale at all points of
![]() $\phi ^{\prime -1}(0) \cap Z$
(for general
$\phi ^{\prime -1}(0) \cap Z$
(for general
![]() $\phi _i$
) and
$\phi _i$
) and
![]() $Z \to X$
is a closed immersion,
$Z \to X$
is a closed immersion,
![]() $\psi $
is unramified at all points above
$\psi $
is unramified at all points above
![]() $0$
and so
$0$
and so
![]() $\psi _0$
is unramified (for general
$\psi _0$
is unramified (for general
![]() $\phi _i$
). Since
$\phi _i$
). Since
![]() $\phi : Z \to \mathbb A^d$
is finite, so is
$\phi : Z \to \mathbb A^d$
is finite, so is
![]() $\psi $
; in fact,
$\psi $
; in fact,
![]() $\phi ^{\prime -1}(0) \cap Z$
is finite over F. By [22, Tags 04XV and 01S4], a morphism is a closed immersion if and only if it is proper, unramified, and radicial; we already know that
$\phi ^{\prime -1}(0) \cap Z$
is finite over F. By [22, Tags 04XV and 01S4], a morphism is a closed immersion if and only if it is proper, unramified, and radicial; we already know that
![]() $\psi _0$
is finite (hence proper) and unramified. Being radicial is fpqc local on the target [22, Tag 02KW], so may be checked after geometric base change. In other words (using that
$\psi _0$
is finite (hence proper) and unramified. Being radicial is fpqc local on the target [22, Tag 02KW], so may be checked after geometric base change. In other words (using that
![]() $\phi ^{\prime -1}(0) \cap Z$
is finite over F), we need the
$\phi ^{\prime -1}(0) \cap Z$
is finite over F), we need the
![]() $\phi _i$
to separate a finite number of specified geometric points. This clearly holds for general
$\phi _i$
to separate a finite number of specified geometric points. This clearly holds for general
![]() $\phi _i$
.
$\phi _i$
.
Proof Proof of Theorem 3.1
If the theorem holds for composable maps f and g, then it holds for
![]() $fg$
. Given
$fg$
. Given
![]() $f: Y \to X$
, we factor it as
$f: Y \to X$
, we factor it as
 $$ \begin{align*} Y \xrightarrow{i} \Gamma_f \xrightarrow{p} X; \end{align*} $$
$$ \begin{align*} Y \xrightarrow{i} \Gamma_f \xrightarrow{p} X; \end{align*} $$
here
![]() $i: Y \to \Gamma _f$
is the graph of f. Then i is a regular immersion and p is smooth. It follows that
$i: Y \to \Gamma _f$
is the graph of f. Then i is a regular immersion and p is smooth. It follows that
![]() $p^{-1}(Z) \subset \Gamma _f$
has codimension
$p^{-1}(Z) \subset \Gamma _f$
has codimension
![]() $\ge d$
(see, e.g., [Reference Grothendieck8, Corollary 6.1.4]). Hence it suffices to prove the result for i and p separately – that is, we may assume that f is either a regular immersion or a smooth morphism. The case of smooth maps was already explained in Remark 3.3, so assume that
$\ge d$
(see, e.g., [Reference Grothendieck8, Corollary 6.1.4]). Hence it suffices to prove the result for i and p separately – that is, we may assume that f is either a regular immersion or a smooth morphism. The case of smooth maps was already explained in Remark 3.3, so assume that
![]() $f: Y \hookrightarrow X$
is a regular immersion. As usual, we may localize in a generic point of
$f: Y \hookrightarrow X$
is a regular immersion. As usual, we may localize in a generic point of
![]() $Z \cap Y$
of codimension d on Y; hence we may assume that
$Z \cap Y$
of codimension d on Y; hence we may assume that
![]() $Z \cap Y = \{z\}$
is a closed point, X is local, and
$Z \cap Y = \{z\}$
is a closed point, X is local, and
![]() $\dim Y = d$
. It follows (e.g., from [22, Tag 00NQ]) that there exists a sequence of codimension
$\dim Y = d$
. It follows (e.g., from [22, Tag 00NQ]) that there exists a sequence of codimension
![]() $1$
embeddings of essentially smooth schemes
$1$
embeddings of essentially smooth schemes
Let
![]() $Z_i = Z \cap Y_i$
. Then
$Z_i = Z \cap Y_i$
. Then
![]() $\dim Z_i \ge \dim Z_{i+1}-1$
[22, Tag 00KW], but
$\dim Z_i \ge \dim Z_{i+1}-1$
[22, Tag 00KW], but
![]() $\dim Z_n = n-d = \dim Z_d + n-d$
, so that
$\dim Z_n = n-d = \dim Z_d + n-d$
, so that
![]() $\dim Z_i = i-d$
for all i. It follows that we may prove the result for each
$\dim Z_i = i-d$
for all i. It follows that we may prove the result for each
![]() $Y_i \hookrightarrow Y_{i+1}$
separately; this is Lemma 3.13.
$Y_i \hookrightarrow Y_{i+1}$
separately; this is Lemma 3.13.
4 Applications
After introducing some notation in §4.1, we identify the heart of
 $\mathcal {SH}^{S^1}\!(k)(d)$
(for
$\mathcal {SH}^{S^1}\!(k)(d)$
(for
![]() $d \ge 3$
) in §4.2. This establishes [Reference Bosch, Lütkebohmert and Raynaud2, Conjecture 6.10]. Finally, in §4.3 we study convergence of the resolution of an
$d \ge 3$
) in §4.2. This establishes [Reference Bosch, Lütkebohmert and Raynaud2, Conjecture 6.10]. Finally, in §4.3 we study convergence of the resolution of an
![]() $S^1$
-spectrum by infinite
$S^1$
-spectrum by infinite
![]() $\mathbb P^1$
-loop spectra arising from the adjunction
$\mathbb P^1$
-loop spectra arising from the adjunction
 $\mathcal {SH}^{S^1}\!(k) \leftrightarrows \mathcal {SH}(k)$
and deduce some conservativity results.
$\mathcal {SH}^{S^1}\!(k) \leftrightarrows \mathcal {SH}(k)$
and deduce some conservativity results.
We also assume that k is perfect; we will restate this assumption with the most important results only.
4.1 Notation and hypotheses
We write
 $\mathcal {SH}^{S^1}\!(k)$
for the category of motivic
$\mathcal {SH}^{S^1}\!(k)$
for the category of motivic
![]() $S^1$
-spectra [Reference Morel16, §4] (i.e., the motivic localization of the category of spectral presheaves on
$S^1$
-spectra [Reference Morel16, §4] (i.e., the motivic localization of the category of spectral presheaves on
![]() ${\mathrm {S}\mathrm {m}}_k$
), and
${\mathrm {S}\mathrm {m}}_k$
), and
 $\mathcal {SH}(k) = \mathcal {SH}^{S^1}\!(k)\left [{\mathbb {G}_m^{\wedge -1}}\right ]$
for the category of motivic spectra [Reference Morel16, §5]. For the stabilization functors, we use the notation
$\mathcal {SH}(k) = \mathcal {SH}^{S^1}\!(k)\left [{\mathbb {G}_m^{\wedge -1}}\right ]$
for the category of motivic spectra [Reference Morel16, §5]. For the stabilization functors, we use the notation
 $$ \begin{align*} {\mathrm{S}\mathrm{m}}_{k*} \xrightarrow{\Sigma^\infty_{S^1}} \mathcal{SH}^{S^1}\!(k) \xrightarrow{\sigma^\infty} \mathcal{SH}(k)^{\text{eff}} \subset \mathcal{SH}(k), \end{align*} $$
$$ \begin{align*} {\mathrm{S}\mathrm{m}}_{k*} \xrightarrow{\Sigma^\infty_{S^1}} \mathcal{SH}^{S^1}\!(k) \xrightarrow{\sigma^\infty} \mathcal{SH}(k)^{\text{eff}} \subset \mathcal{SH}(k), \end{align*} $$
and we denote by
![]() $\omega ^\infty $
the right adjoint of
$\omega ^\infty $
the right adjoint of
![]() $\sigma ^\infty $
. Here
$\sigma ^\infty $
. Here
![]() $\mathcal {SH}(k)^{\text {eff}}$
is the localizing subcategory generated by the image of
$\mathcal {SH}(k)^{\text {eff}}$
is the localizing subcategory generated by the image of
![]() $\sigma ^\infty $
.
$\sigma ^\infty $
.
There are localizing subcategories
 $$ \begin{align*} \mathcal{SH}^{S^1}\!(k) \supset \mathcal{SH}^{S^1}\!(k)(1) \supset \cdots \supset \mathcal{SH}^{S^1}\!(k)(d) \supset \cdots; \end{align*} $$
$$ \begin{align*} \mathcal{SH}^{S^1}\!(k) \supset \mathcal{SH}^{S^1}\!(k)(1) \supset \cdots \supset \mathcal{SH}^{S^1}\!(k)(d) \supset \cdots; \end{align*} $$
here
 $\mathcal {SH}^{S^1}\!(k)(d)$
is generated by
$\mathcal {SH}^{S^1}\!(k)(d)$
is generated by
 $\Sigma ^\infty _{S^1} X_+ \wedge {\mathbb {G}_m^{\wedge d}}$
for
$\Sigma ^\infty _{S^1} X_+ \wedge {\mathbb {G}_m^{\wedge d}}$
for
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
. The inclusion
$X \in {\mathrm {S}\mathrm {m}}_k$
. The inclusion
 $\mathcal {SH}^{S^1}\!(k)(d) \subset \mathcal {SH}^{S^1}\!(k)$
has a right adjoint which we denote by
$\mathcal {SH}^{S^1}\!(k)(d) \subset \mathcal {SH}^{S^1}\!(k)$
has a right adjoint which we denote by
![]() $f_d$
.Footnote
8
There are canonical cofiber sequences
$f_d$
.Footnote
8
There are canonical cofiber sequences
![]() $f_{d+1} \to f_d \to s_d$
defining the functors
$f_{d+1} \to f_d \to s_d$
defining the functors
![]() $s_d$
. There is a similar filtration of
$s_d$
. There is a similar filtration of
![]() $\mathcal {SH}(k)^{\text {eff}}$
, given by
$\mathcal {SH}(k)^{\text {eff}}$
, given by
![]() $\mathcal {SH}(k)^{\text {eff}}(d) := \mathcal {SH}(k)^{\text {eff}} \wedge {\mathbb {G}_m^{\wedge d}}$
, and the right adjoints (resp., cofibers) are again denoted by
$\mathcal {SH}(k)^{\text {eff}}(d) := \mathcal {SH}(k)^{\text {eff}} \wedge {\mathbb {G}_m^{\wedge d}}$
, and the right adjoints (resp., cofibers) are again denoted by
![]() $f_d$
(resp.,
$f_d$
(resp.,
![]() $s_d$
). See [Reference Levine10, 23] or [Reference Bosch, Lütkebohmert and Raynaud2, §6.1] for more details on these functors.
$s_d$
). See [Reference Levine10, 23] or [Reference Bosch, Lütkebohmert and Raynaud2, §6.1] for more details on these functors.
Recall that
 $\mathcal {SH}^{S^1}\!(k)$
has a t-structure with nonnegative part generated by
$\mathcal {SH}^{S^1}\!(k)$
has a t-structure with nonnegative part generated by
![]() $\Sigma ^\infty _{S^1} X_+$
for
$\Sigma ^\infty _{S^1} X_+$
for
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
; its heart canonically identifies with
$X \in {\mathrm {S}\mathrm {m}}_k$
; its heart canonically identifies with
![]() $\mathbf {HI}(k)$
[Reference Morel16, Lemma 4.3.7(2)]. We denote by
$\mathbf {HI}(k)$
[Reference Morel16, Lemma 4.3.7(2)]. We denote by
![]() $E_{\ge 0}$
,
$E_{\ge 0}$
,
![]() $E_{\le 0}$
, and
$E_{\le 0}$
, and
![]() $\underline {\pi }_0 E$
the truncations and homotopy sheaves, respectively. The categories
$\underline {\pi }_0 E$
the truncations and homotopy sheaves, respectively. The categories
 $\mathcal {SH}^{S^1}\!(k)(d)$
,
$\mathcal {SH}^{S^1}\!(k)(d)$
,
![]() $\mathcal {SH}(k)$
, and
$\mathcal {SH}(k)$
, and
![]() $\mathcal {SH}(k)^{\text {eff}}(d)$
have related t-structures, with nonnegative parts generated by
$\mathcal {SH}(k)^{\text {eff}}(d)$
have related t-structures, with nonnegative parts generated by
![]() $X_+ \wedge {\mathbb {G}_m^{\wedge d}}$
.
$X_+ \wedge {\mathbb {G}_m^{\wedge d}}$
.
Recall from [Reference Bosch, Lütkebohmert and Raynaud2, §5.1] the notion of a presheaf with
![]() $\mathbb A^1$
-transfers. This is just a presheaf F on
$\mathbb A^1$
-transfers. This is just a presheaf F on
![]() ${\mathrm {S}\mathrm {m}}_k$
together with, for every finitely generated field
${\mathrm {S}\mathrm {m}}_k$
together with, for every finitely generated field
![]() $K/k$
, a
$K/k$
, a
![]() $GW(K)$
-module structure on
$GW(K)$
-module structure on
![]() $F(K)$
, and for every finite monogeneic extension
$F(K)$
, and for every finite monogeneic extension
![]() $K(x)/K$
, a transfer
$K(x)/K$
, a transfer
![]() $\tau _x: F(K(x)) \to F(K)$
. The category
$\tau _x: F(K(x)) \to F(K)$
. The category
![]() $\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$
embeds fully faithfully into the category of presheaves with
$\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$
embeds fully faithfully into the category of presheaves with
![]() $\mathbb A^1$
-transfers [Reference Bosch, Lütkebohmert and Raynaud2, Corollary 5.17] (morphisms in this category are given by morphisms of presheaves compatible with the
$\mathbb A^1$
-transfers [Reference Bosch, Lütkebohmert and Raynaud2, Corollary 5.17] (morphisms in this category are given by morphisms of presheaves compatible with the
![]() $GW$
-module structures and transfers). Given a presheaf with
$GW$
-module structures and transfers). Given a presheaf with
![]() $\mathbb A^1$
-transfers M, we say that the transfers extend to framed transfers if M is in the essential image of this embedding. Recall also that Morel has shown that if
$\mathbb A^1$
-transfers M, we say that the transfers extend to framed transfers if M is in the essential image of this embedding. Recall also that Morel has shown that if
![]() $M \in \mathbf {HI}(k)$
and
$M \in \mathbf {HI}(k)$
and
![]() $d>0$
, then
$d>0$
, then
![]() $M_{-d}$
canonically extends to a presheaf with
$M_{-d}$
canonically extends to a presheaf with
![]() $\mathbb A^1$
-transfers (see §2.1.8 or [Reference Bosch, Lütkebohmert and Raynaud2, Example 5.2]).
$\mathbb A^1$
-transfers (see §2.1.8 or [Reference Bosch, Lütkebohmert and Raynaud2, Example 5.2]).
Definition 4.1. Let k be a perfect field and
![]() $d>0$
.
$d>0$
.
-
(1) Set
 $M \in \mathbf {HI}(k)$
. We shall say that hypothesis
$M \in \mathbf {HI}(k)$
. We shall say that hypothesis
 $T_d(M)$
holds if the canonical
$T_d(M)$
holds if the canonical
 $\mathbb A^1$
-transfers on
$\mathbb A^1$
-transfers on
 $M_{-d}$
extend to framed transfers. We shall say that hypothesis
$M_{-d}$
extend to framed transfers. We shall say that hypothesis
 $T_d(k)$
holds if
$T_d(k)$
holds if
 $T_d(M)$
holds for all
$T_d(M)$
holds for all
 $M \in \mathbf {HI}(k)$
.
$M \in \mathbf {HI}(k)$
. -
(2) We shall say that hypothesis
 $S_d(k)$
holds if for any
$S_d(k)$
holds if for any
 $E \in \mathcal {SH}^{S^1}\!(k)$
and
$E \in \mathcal {SH}^{S^1}\!(k)$
and
 $i \in \mathbb {Z}$
, the spectrum
$i \in \mathbb {Z}$
, the spectrum
 $f_d \underline {\pi }_i s_d E$
is in the essential image of
$f_d \underline {\pi }_i s_d E$
is in the essential image of
 $\omega ^\infty : \mathcal {SH}(k) \to \mathcal {SH}^{S^1}\!(k)$
.
$\omega ^\infty : \mathcal {SH}(k) \to \mathcal {SH}^{S^1}\!(k)$
.
Remark 4.2. If k is perfect, then
![]() $T_d(k)$
holds for any
$T_d(k)$
holds for any
![]() $d \ge 3$
, and if
$d \ge 3$
, and if
![]() $char(k) = 0$
, then
$char(k) = 0$
, then
![]() $T_2(k)$
also holds [Reference Bosch, Lütkebohmert and Raynaud2, Theorem 5.19].
$T_2(k)$
also holds [Reference Bosch, Lütkebohmert and Raynaud2, Theorem 5.19].
Remark 4.3. We speculate that
![]() $T_1(k)$
holds for any perfect field.
$T_1(k)$
holds for any perfect field.
Remark 4.4. If
![]() $f: \mathrm {Spec}(l) \to \mathrm {Spec}(k)$
is an algebraic extension (automatically separable) and
$f: \mathrm {Spec}(l) \to \mathrm {Spec}(k)$
is an algebraic extension (automatically separable) and
![]() $M \in \mathbf {HI}(k)$
such that
$M \in \mathbf {HI}(k)$
such that
![]() $T_d(M)$
holds, then
$T_d(M)$
holds, then
![]() $T_d(f^*M)$
also holds. This is obvious for f finite, and the general case follows by continuity and essentially smooth base change.
$T_d(f^*M)$
also holds. This is obvious for f finite, and the general case follows by continuity and essentially smooth base change.
Theorem 4.5. Levine [Reference Levine11]
Let
![]() $char(k) = 0$
. Then
$char(k) = 0$
. Then
![]() $S_d(k)$
holds for any
$S_d(k)$
holds for any
![]() $d>0$
.
$d>0$
.
Proof. This is essentially [Reference Levine11, Theorem 2]; we just have to show that
 $$ \begin{align*} s_{p,n} E \simeq f_n \Sigma^{p+n} \underline{\pi}_{p+n} s_n E. \end{align*} $$
$$ \begin{align*} s_{p,n} E \simeq f_n \Sigma^{p+n} \underline{\pi}_{p+n} s_n E. \end{align*} $$
By definition [Reference Levine11, main construction (9.2)],
![]() $s_{p,n} E(X)$
is the realization of (a rectification of) the simplicial object
$s_{p,n} E(X)$
is the realization of (a rectification of) the simplicial object
![]() $\Sigma ^p\pi _p (s_n E)^{(n)}(X, \bullet )$
; here
$\Sigma ^p\pi _p (s_n E)^{(n)}(X, \bullet )$
; here
![]() $(s_n E)^{(n)}(X, \bullet )$
is the homotopy coniveau tower model of
$(s_n E)^{(n)}(X, \bullet )$
is the homotopy coniveau tower model of
![]() $f_n s_n E \simeq s_n E$
, and
$f_n s_n E \simeq s_n E$
, and
![]() $\pi _p$
just means taking the pth Eilenberg–MacLane spectrum of the (levelwise) ordinary spectrum
$\pi _p$
just means taking the pth Eilenberg–MacLane spectrum of the (levelwise) ordinary spectrum
![]() $(s_n E)^{(n)}(X, \bullet )$
.
$(s_n E)^{(n)}(X, \bullet )$
.
The map
![]() $(s_n E)_{\ge n+p} \to s_n E$
of spectral sheaves induces a map
$(s_n E)_{\ge n+p} \to s_n E$
of spectral sheaves induces a map
 $$ \begin{align*} \alpha_p: \left((s_n E)_{\ge p+n}\right)^{(n)}(\mathord-, \bullet) \to (s_n E)^{(n)}(\mathord-, \bullet) \end{align*} $$
$$ \begin{align*} \alpha_p: \left((s_n E)_{\ge p+n}\right)^{(n)}(\mathord-, \bullet) \to (s_n E)^{(n)}(\mathord-, \bullet) \end{align*} $$
of simplicial spectral presheaves. We claim that
![]() $\alpha _p$
induces an isomorphism on
$\alpha _p$
induces an isomorphism on
![]() $\pi _i$
for
$\pi _i$
for
![]() $i \ge p$
, and that the source has
$i \ge p$
, and that the source has
![]() $\pi _i = 0$
for
$\pi _i = 0$
for
![]() $i < p$
. This yields an equivalence
$i < p$
. This yields an equivalence
 $$ \begin{align*} \left((s_n E)_{\ge p+n}\right)^{(n)}(\mathord-, \bullet) \simeq \tau_{\ge p}(s_n E)^{(n)}(\mathord-, \bullet), \end{align*} $$
$$ \begin{align*} \left((s_n E)_{\ge p+n}\right)^{(n)}(\mathord-, \bullet) \simeq \tau_{\ge p}(s_n E)^{(n)}(\mathord-, \bullet), \end{align*} $$
where
![]() $\tau _{\ge p}$
just means levelwise truncation of the simplicial presheaf of spectra. Taking cofibers, we obtain
$\tau _{\ge p}$
just means levelwise truncation of the simplicial presheaf of spectra. Taking cofibers, we obtain
 $$ \begin{align*} \left(\Sigma^{p+n} \underline{\pi}_{p+n} s_n E\right)^{(n)}(\mathord-, \bullet) \simeq \Sigma^p \pi_p(s_n E)^{(n)}(\mathord-, \bullet), \end{align*} $$
$$ \begin{align*} \left(\Sigma^{p+n} \underline{\pi}_{p+n} s_n E\right)^{(n)}(\mathord-, \bullet) \simeq \Sigma^p \pi_p(s_n E)^{(n)}(\mathord-, \bullet), \end{align*} $$
which is what we set out to prove (using [Reference Levine10, Theorem 7.1.1]).
It is hence enough to prove the claim. Thus let
![]() $X \in {\mathrm {S}\mathrm {m}}_k$
and
$X \in {\mathrm {S}\mathrm {m}}_k$
and
![]() $W \subset \mathbb A^m_X$
have codimension
$W \subset \mathbb A^m_X$
have codimension
![]() $\ge n$
. The definition of the homotopy coniveau tower (recalled, e.g., in [Reference Levine11, §9]) implies that it is enough to show that
$\ge n$
. The definition of the homotopy coniveau tower (recalled, e.g., in [Reference Levine11, §9]) implies that it is enough to show that
 $$ \begin{align*} H^{-i}_W\left(\mathbb A^m_X, s_n E\right) \simeq H^{-i}_W\left(\mathbb A^m_X, (s_n E)_{\ge n+p}\right) \text{ for } i\ge p \end{align*} $$
$$ \begin{align*} H^{-i}_W\left(\mathbb A^m_X, s_n E\right) \simeq H^{-i}_W\left(\mathbb A^m_X, (s_n E)_{\ge n+p}\right) \text{ for } i\ge p \end{align*} $$
and
 $$ \begin{align*} H^{-i}_W\left(\mathbb A^m_X, (s_n E)_{\ge n+p}\right) = 0 \text{ for } i < p. \end{align*} $$
$$ \begin{align*} H^{-i}_W\left(\mathbb A^m_X, (s_n E)_{\ge n+p}\right) = 0 \text{ for } i < p. \end{align*} $$
Considering the (strongly convergent) descent spectral sequence (for
 $F \in \mathcal {SH}^{S^1}\!(k)$
)
$F \in \mathcal {SH}^{S^1}\!(k)$
)
 $$ \begin{align*} H^p_W\left(\mathbb A^m_X, \underline{\pi}_q F\right) \Rightarrow H^{p-q}_W\left(\mathbb A^m_X, F\right), \end{align*} $$
$$ \begin{align*} H^p_W\left(\mathbb A^m_X, \underline{\pi}_q F\right) \Rightarrow H^{p-q}_W\left(\mathbb A^m_X, F\right), \end{align*} $$
for this it suffices to show that for
![]() $j \in \mathbb {Z}$
we have
$j \in \mathbb {Z}$
we have
 $$ \begin{align*} H^i_W\left(\mathbb A^m_X, \underline{\pi}_j s_n E\right) = 0 \text{ for } i \ne n. \end{align*} $$
$$ \begin{align*} H^i_W\left(\mathbb A^m_X, \underline{\pi}_j s_n E\right) = 0 \text{ for } i \ne n. \end{align*} $$
We can compute this cohomology group using the Rost–Schmid resolution; since W has codimension
![]() $\ge n$
, the vanishing follows from the observation that
$\ge n$
, the vanishing follows from the observation that
![]() $\underline {\pi }_j(s_n E)_{-i} = 0$
for
$\underline {\pi }_j(s_n E)_{-i} = 0$
for
![]() $i> n$
, which holds because
$i> n$
, which holds because
 $\Omega _{{\mathbb {G}_m}}^{i} s_n E \simeq 0$
(for
$\Omega _{{\mathbb {G}_m}}^{i} s_n E \simeq 0$
(for
![]() $i>n$
) by definition.
$i>n$
) by definition.
4.2 The heart of
 $\mathcal {SH}^{S^1}\!(k)(d)$
$\mathcal {SH}^{S^1}\!(k)(d)$
Consider the adjunction
 $$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k) \leftrightarrows \mathcal{SH}(k): \omega^\infty. \end{align*} $$
$$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k) \leftrightarrows \mathcal{SH}(k): \omega^\infty. \end{align*} $$
Then
 $\sigma ^\infty \left (\mathcal {SH}^{S^1}\!(k)(d)\right ) \subset \mathcal {SH}(k)^{\text {eff}}(d)$
and
$\sigma ^\infty \left (\mathcal {SH}^{S^1}\!(k)(d)\right ) \subset \mathcal {SH}(k)^{\text {eff}}(d)$
and
 $\sigma ^\infty \left (\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}\right ) \subset \mathcal {SH}(k)^{\text {eff}}(d)_{\ge 0}$
, for any
$\sigma ^\infty \left (\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}\right ) \subset \mathcal {SH}(k)^{\text {eff}}(d)_{\ge 0}$
, for any
![]() $d \ge 0$
. Moreover, it follows from [Reference Bosch, Lütkebohmert and Raynaud2, Lemmas 6.1(2) and 6.2(1,2)] that
$d \ge 0$
. Moreover, it follows from [Reference Bosch, Lütkebohmert and Raynaud2, Lemmas 6.1(2) and 6.2(1,2)] that
 $\omega ^\infty \left (\mathcal {SH}(k)^{\text {eff}}(d)\right ) \subset \mathcal {SH}^{S^1}\!(k)(d)$
and
$\omega ^\infty \left (\mathcal {SH}(k)^{\text {eff}}(d)\right ) \subset \mathcal {SH}^{S^1}\!(k)(d)$
and
 $\omega ^\infty \left (\mathcal {SH}(k)^{\text {eff}}(d)_{\ge 0}\right ) \subset \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
. This implies that there is an induced adjunction
$\omega ^\infty \left (\mathcal {SH}(k)^{\text {eff}}(d)_{\ge 0}\right ) \subset \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
. This implies that there is an induced adjunction
 $$ \begin{align*} \pi_0^d \sigma^\infty: \mathcal{SH}^{S^1}\!(k)(d)^\heartsuit \leftrightarrows \mathcal{SH}(k)^{\text{eff}}(d)^\heartsuit: \omega^\infty, \end{align*} $$
$$ \begin{align*} \pi_0^d \sigma^\infty: \mathcal{SH}^{S^1}\!(k)(d)^\heartsuit \leftrightarrows \mathcal{SH}(k)^{\text{eff}}(d)^\heartsuit: \omega^\infty, \end{align*} $$
where
![]() $\pi _0^d$
denotes the truncation functor in the t-structure on
$\pi _0^d$
denotes the truncation functor in the t-structure on
![]() $\mathcal {SH}(k)^{\text {eff}}(d)$
.
$\mathcal {SH}(k)^{\text {eff}}(d)$
.
Theorem 4.6. Let k be a perfect field such that
![]() $T_d(k)$
holds. Then the functor
$T_d(k)$
holds. Then the functor
 $\omega ^{\infty }: \mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit \to \mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
is an equivalence of categories.
$\omega ^{\infty }: \mathcal {SH}(k)^{\text {eff}}(d)^\heartsuit \to \mathcal {SH}^{S^1}\!(k)(d)^\heartsuit $
is an equivalence of categories.
This establishes [Reference Bosch, Lütkebohmert and Raynaud2, Conjecture 6.10] (for
![]() $n=d$
).
$n=d$
).
Proof. The functor is fully faithful by [Reference Bosch, Lütkebohmert and Raynaud2, Theorem 6.9]; it hence suffices to prove essential surjectivity. We shall prove the following more precise statement: if
![]() $M \in \mathbf {HI}(k)$
and
$M \in \mathbf {HI}(k)$
and
![]() $T_d(M)$
holds, then M is in the essential image of
$T_d(M)$
holds, then M is in the essential image of
![]() $\omega ^\infty $
.
$\omega ^\infty $
.
We first prove this assuming that k is infinite. We have
![]() $\underline {\pi }_i(M)_{-d} = 0$
for
$\underline {\pi }_i(M)_{-d} = 0$
for
![]() $i \ne 0$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)], and hence the canonical map
$i \ne 0$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)], and hence the canonical map
![]() $M \to f_d \underline {\pi }_0 M$
is an equivalence (indeed, it induces an equivalence on
$M \to f_d \underline {\pi }_0 M$
is an equivalence (indeed, it induces an equivalence on
![]() $\underline {\pi }_i(\mathord -)_{-d}$
for every i, and this detects equivalence in
$\underline {\pi }_i(\mathord -)_{-d}$
for every i, and this detects equivalence in
 $\mathcal {SH}^{S^1}\!(k)(d)$
by [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.1(1)]). By assumption, the
$\mathcal {SH}^{S^1}\!(k)(d)$
by [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.1(1)]). By assumption, the
![]() $\mathbb A^1$
-transfers on
$\mathbb A^1$
-transfers on
![]() $\underline {\pi }_0(M)_{-d}$
extend to framed transfers; hence there exists
$\underline {\pi }_0(M)_{-d}$
extend to framed transfers; hence there exists
![]() $\tilde M \in \mathcal {SH}(k)^{{\text {eff}}\heartsuit }$
such that
$\tilde M \in \mathcal {SH}(k)^{{\text {eff}}\heartsuit }$
such that
 $\omega ^\infty \left (\tilde M\right )_{-d} \simeq \underline {\pi }_0(M)_{-d}$
as presheaves with
$\omega ^\infty \left (\tilde M\right )_{-d} \simeq \underline {\pi }_0(M)_{-d}$
as presheaves with
![]() $\mathbb A^1$
-transfers. By Lemma 4.7 (this is where we use the assumption that k is infinite), this implies that
$\mathbb A^1$
-transfers. By Lemma 4.7 (this is where we use the assumption that k is infinite), this implies that
 $f_d \omega ^\infty \left (\tilde M\right ) \simeq f_d \underline {\pi }_0(M)$
. It follows from [Reference Levine10, Theorem 9.0.3] that
$f_d \omega ^\infty \left (\tilde M\right ) \simeq f_d \underline {\pi }_0(M)$
. It follows from [Reference Levine10, Theorem 9.0.3] that
![]() $f_d$
commutes with
$f_d$
commutes with
![]() $\omega ^\infty $
; we thus find that
$\omega ^\infty $
; we thus find that
 $$ \begin{align*} M \simeq f_d \underline{\pi}_0 M \simeq f_d \omega^\infty\left(\tilde M\right) \simeq \omega^\infty f_d \tilde M. \end{align*} $$
$$ \begin{align*} M \simeq f_d \underline{\pi}_0 M \simeq f_d \omega^\infty\left(\tilde M\right) \simeq \omega^\infty f_d \tilde M. \end{align*} $$
The claim is thus proved for k infinite.
Now let k be finite and
![]() $M \in \mathbf {HI}(k)$
such that
$M \in \mathbf {HI}(k)$
such that
![]() $T_d(M)$
holds. Since
$T_d(M)$
holds. Since
![]() $\omega ^\infty $
is fully faithful, M is in the essential image of
$\omega ^\infty $
is fully faithful, M is in the essential image of
![]() $\omega ^\infty $
if and only if the canonical map
$\omega ^\infty $
if and only if the canonical map
![]() $M \to \omega ^\infty \sigma ^{\infty \heartsuit } M$
is an isomorphism. The functors
$M \to \omega ^\infty \sigma ^{\infty \heartsuit } M$
is an isomorphism. The functors
![]() $\omega ^\infty $
and
$\omega ^\infty $
and
![]() $\sigma ^{\infty \heartsuit }$
commute with essentially smooth base change. Let
$\sigma ^{\infty \heartsuit }$
commute with essentially smooth base change. Let
![]() $f: \mathrm {Spec}(l) \to \mathrm {Spec}(k)$
be an infinite algebraic p-extension of k, for some prime p. Using Lemma 4.8 we reduce to proving that
$f: \mathrm {Spec}(l) \to \mathrm {Spec}(k)$
be an infinite algebraic p-extension of k, for some prime p. Using Lemma 4.8 we reduce to proving that
![]() $f^*M$
is in the essential image of
$f^*M$
is in the essential image of
![]() $\omega ^\infty $
. By Remark 4.4,
$\omega ^\infty $
. By Remark 4.4,
![]() $T_d(f^*M)$
holds, and thus we are reduced to what was already established.
$T_d(f^*M)$
holds, and thus we are reduced to what was already established.
This concludes the proof.
Lemma 4.7. Let k be an infinite perfect field,
![]() $M, N \in \mathbf {HI}(k)$
, and
$M, N \in \mathbf {HI}(k)$
, and
![]() $d>0$
. Suppose that
$d>0$
. Suppose that
![]() $T_d(M)$
holds. Any isomorphism
$T_d(M)$
holds. Any isomorphism
![]() $M_{-d} \simeq N_{-d}$
respecting the
$M_{-d} \simeq N_{-d}$
respecting the
![]() $\mathbb A^1$
-transfers yields an equivalence
$\mathbb A^1$
-transfers yields an equivalence
![]() $f_d M \simeq f_d N$
.
$f_d M \simeq f_d N$
.
Proof. We have
![]() $f_d M \simeq M^{(d)}$
[Reference Levine10, Theorem 7.1.1] (this is where we use the assumption that k is infinite). As explained in [Reference Bosch, Lütkebohmert and Raynaud2, Remark 4.17], the (truncated) BLRS complex of M provides a model of
$f_d M \simeq M^{(d)}$
[Reference Levine10, Theorem 7.1.1] (this is where we use the assumption that k is infinite). As explained in [Reference Bosch, Lütkebohmert and Raynaud2, Remark 4.17], the (truncated) BLRS complex of M provides a model of
![]() $M^{(d)}$
which depends only on
$M^{(d)}$
which depends only on
![]() $M_{-d}$
as a presheaf of
$M_{-d}$
as a presheaf of
![]() $GW$
-modules together with the maps
$GW$
-modules together with the maps
 $f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
for
$f^*: H^d_Z(X, M) \to H^d_{f^{-1}(Z)}(Y, M)$
for
![]() $f: Y \to X \in {\mathrm {S}\mathrm {m}}_k$
, with
$f: Y \to X \in {\mathrm {S}\mathrm {m}}_k$
, with
![]() $Z \subset X$
closed of codimension
$Z \subset X$
closed of codimension
![]() $\ge d$
such that
$\ge d$
such that
![]() $f^{-1}(Z)$
also has codimension
$f^{-1}(Z)$
also has codimension
![]() $\ge d$
. (In order to apply this remark, we need to know that
$\ge d$
. (In order to apply this remark, we need to know that
![]() $M_{-d}$
has framed transfers – see, e.g., [Reference Bosch, Lütkebohmert and Raynaud2, Proposition 4.14]); this is the only reason for assuming
$M_{-d}$
has framed transfers – see, e.g., [Reference Bosch, Lütkebohmert and Raynaud2, Proposition 4.14]); this is the only reason for assuming
![]() $T_d(k)$
.) Theorem 3.1 shows that
$T_d(k)$
.) Theorem 3.1 shows that
![]() $f^*$
depends only on
$f^*$
depends only on
![]() $M_{-d}$
as a presheaf with
$M_{-d}$
as a presheaf with
![]() $\mathbb A^1$
-transfers. The result follows.
$\mathbb A^1$
-transfers. The result follows.
Lemma 4.8. Let k be a perfect field and
![]() $k_p/k$
(resp.,
$k_p/k$
(resp.,
![]() $k_q/k$
) a separable algebraic p-extension (resp., q-extension), for primes
$k_q/k$
) a separable algebraic p-extension (resp., q-extension), for primes
![]() $p \ne q$
. Set
$p \ne q$
. Set
 $\alpha : E \to F \in \mathcal {SH}^{S^1}\!(k)(d)$
such that
$\alpha : E \to F \in \mathcal {SH}^{S^1}\!(k)(d)$
such that
![]() $T_d(M)$
holds for any homotopy sheaf M of E or F. If the image of
$T_d(M)$
holds for any homotopy sheaf M of E or F. If the image of
![]() $\alpha $
in
$\alpha $
in
 $\mathcal {SH}^{S^1}\!\left (k_p\right )(d) \times \mathcal {SH}^{S^1}\!\left (k_q\right )(d)$
is an equivalence, then so is
$\mathcal {SH}^{S^1}\!\left (k_p\right )(d) \times \mathcal {SH}^{S^1}\!\left (k_q\right )(d)$
is an equivalence, then so is
![]() $\alpha $
.
$\alpha $
.
Proof. It suffices to prove that
 $\Omega ^d_{\mathbb {G}_m}(\alpha )$
is an equivalence [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.1(1)] – that is, that
$\Omega ^d_{\mathbb {G}_m}(\alpha )$
is an equivalence [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.1(1)] – that is, that
![]() $\underline {\pi }_i(\alpha )_{-d}$
is an isomorphism for all i. By assumption, this is a morphism between sheaves admitting framed transfers, and by [Reference Bosch, Lütkebohmert and Raynaud2, Corollary 5.17] the morphism preserves the transfers. The result thus follows from [Reference Elmanto, Hoyois, Khan, Sosnilo and Yakerson5, Corollary B.2.5] (using the fact that essentially smooth base change commutes with
$\underline {\pi }_i(\alpha )_{-d}$
is an isomorphism for all i. By assumption, this is a morphism between sheaves admitting framed transfers, and by [Reference Bosch, Lütkebohmert and Raynaud2, Corollary 5.17] the morphism preserves the transfers. The result thus follows from [Reference Elmanto, Hoyois, Khan, Sosnilo and Yakerson5, Corollary B.2.5] (using the fact that essentially smooth base change commutes with
 $\Omega ^d_{\mathbb {G}_m}$
).
$\Omega ^d_{\mathbb {G}_m}$
).
The following is our degree
![]() $0\; {\mathbb {G}_m}$
-Freudenthal theorem:
$0\; {\mathbb {G}_m}$
-Freudenthal theorem:
Corollary 4.9. Suppose that
![]() $T_d(k)$
holds.
$T_d(k)$
holds.
-
(1) Set
 $E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(d)$
. Then
$E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(d)$
. Then  $$ \begin{align*} \underline{\pi}_0(E) \simeq \underline{\pi}_0(\omega^\infty \sigma^\infty E). \end{align*} $$
$$ \begin{align*} \underline{\pi}_0(E) \simeq \underline{\pi}_0(\omega^\infty \sigma^\infty E). \end{align*} $$
-
(2) Set
 $E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
. Then
$E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
. Then  $$ \begin{align*} \underline{\pi}_0(\omega^\infty \sigma^\infty E) \simeq \underline{\pi}_0\left({\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d}. \end{align*} $$
$$ \begin{align*} \underline{\pi}_0(\omega^\infty \sigma^\infty E) \simeq \underline{\pi}_0\left({\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d}. \end{align*} $$
In particular, this holds for
![]() $d \ge 3$
if k is perfect, and for
$d \ge 3$
if k is perfect, and for
![]() $d \ge 2$
if
$d \ge 2$
if
![]() $char(k) = 0$
.
$char(k) = 0$
.
Proof. (1) We have
 $E \in \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)]. Write
$E \in \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)]. Write
![]() $\pi _0^d$
for the homotopy object in the t-structure on
$\pi _0^d$
for the homotopy object in the t-structure on
 $\mathcal {SH}^{S^1}\!(k)(d)$
. Then since
$\mathcal {SH}^{S^1}\!(k)(d)$
. Then since
![]() $\sigma ^\infty $
and
$\sigma ^\infty $
and
![]() $\omega ^\infty $
are both right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1,2)], we learn from Theorem 4.6 that
$\omega ^\infty $
are both right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1,2)], we learn from Theorem 4.6 that
Since
 $\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0} \subset \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
(by construction), we have
$\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0} \subset \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
(by construction), we have
![]() $\underline {\pi }_0 \pi _0^d \simeq \underline {\pi }_0$
(when applied to objects in
$\underline {\pi }_0 \pi _0^d \simeq \underline {\pi }_0$
(when applied to objects in
 $\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
), and hence the result follows by applying
$\mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
), and hence the result follows by applying
![]() $\underline {\pi }_0$
to
$\underline {\pi }_0$
to
![]() $(*)$
.
$(*)$
.
(2) We have
 $$ \begin{align*} \underline{\pi}_0(\omega^\infty \sigma^\infty E) &\simeq \underline{\pi}_0\left(\omega^\infty \Omega_{{\mathbb{G}_m}}^d \Sigma_{\mathbb{G}_m}^d \sigma^\infty E\right) \\ &\simeq \underline{\pi}_0\left(\Omega_{{\mathbb{G}_m}}^d \omega^\infty \sigma^\infty \Sigma_{\mathbb{G}_m}^d E\right) \\ &\simeq \underline{\pi}_0\left(\omega^\infty \sigma^\infty {\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d} \\ &\stackrel{(1)}{\simeq} \underline{\pi}_0\left({\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d}. \end{align*} $$
$$ \begin{align*} \underline{\pi}_0(\omega^\infty \sigma^\infty E) &\simeq \underline{\pi}_0\left(\omega^\infty \Omega_{{\mathbb{G}_m}}^d \Sigma_{\mathbb{G}_m}^d \sigma^\infty E\right) \\ &\simeq \underline{\pi}_0\left(\Omega_{{\mathbb{G}_m}}^d \omega^\infty \sigma^\infty \Sigma_{\mathbb{G}_m}^d E\right) \\ &\simeq \underline{\pi}_0\left(\omega^\infty \sigma^\infty {\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d} \\ &\stackrel{(1)}{\simeq} \underline{\pi}_0\left({\mathbb{G}_m^{\wedge d}} \wedge E\right)_{-d}. \end{align*} $$
4.3 Canonical resolutions
In this section we will freely use the language of
![]() $\infty $
-categories as set out in [Reference Lurie13, Reference Lurie12].
$\infty $
-categories as set out in [Reference Lurie13, Reference Lurie12].
Given any adjunction
![]() $F: \mathcal C \leftrightarrows \mathcal D: G$
of
$F: \mathcal C \leftrightarrows \mathcal D: G$
of
![]() $\infty $
-categories, there is a monad structure on
$\infty $
-categories, there is a monad structure on
![]() $GF$
[Reference Lurie12, Proposition 4.7.4.3]. Hence for
$GF$
[Reference Lurie12, Proposition 4.7.4.3]. Hence for
![]() $E \in \mathcal C$
there is a canonical ‘triple resolution’
$E \in \mathcal C$
there is a canonical ‘triple resolution’
![]() $E \to E^\bullet $
, where
$E \to E^\bullet $
, where
![]() $E^\bullet $
denotes a cosimplicial object with
$E^\bullet $
denotes a cosimplicial object with
![]() $E^n = (GF)^{\circ (n+1)}(E)$
. In more detail, by the definition of a monad,
$E^n = (GF)^{\circ (n+1)}(E)$
. In more detail, by the definition of a monad,
![]() $GF$
promotes to an
$GF$
promotes to an
![]() $\mathcal E_1$
-algebra in
$\mathcal E_1$
-algebra in
![]() $\mathrm {Fun}(\mathcal C, \mathcal C)$
under the composition monoidal structure, and then [Reference Mathew, Naumann and Noel15, Construction 2.7] yields an augmented cosimplical object in
$\mathrm {Fun}(\mathcal C, \mathcal C)$
under the composition monoidal structure, and then [Reference Mathew, Naumann and Noel15, Construction 2.7] yields an augmented cosimplical object in
![]() $\mathrm {Fun}(\mathcal C, \mathcal C)$
; the triple resolution is obtained by applying this cosimplicial endofunctor to E. This also makes it clear that the triple resolution is functorial in E.
$\mathrm {Fun}(\mathcal C, \mathcal C)$
; the triple resolution is obtained by applying this cosimplicial endofunctor to E. This also makes it clear that the triple resolution is functorial in E.
Applying this to the stabilization adjunction
 $\sigma ^\infty : \mathcal {SH}^{S^1}\!(k) \leftrightarrows \mathcal {SH}(k): \omega ^\infty $
, we obtain the canonical resolution
$\sigma ^\infty : \mathcal {SH}^{S^1}\!(k) \leftrightarrows \mathcal {SH}(k): \omega ^\infty $
, we obtain the canonical resolution
 $$ \begin{align*} E \to E^\wedge := \operatorname*{\mathrm{lim}}_{\Delta}\left[(\omega^\infty \sigma^\infty)^{\circ (\bullet + 1)} E\right], \end{align*} $$
$$ \begin{align*} E \to E^\wedge := \operatorname*{\mathrm{lim}}_{\Delta}\left[(\omega^\infty \sigma^\infty)^{\circ (\bullet + 1)} E\right], \end{align*} $$
functorially in E.
Definition 4.10. We say that the canonical resolution converges for E if this morphism is an equivalence.
Example 4.11. The canonical resolution converges if E is in the essential image of
![]() $\omega ^\infty $
, since then the cosimplicial object is split.
$\omega ^\infty $
, since then the cosimplicial object is split.
Example 4.12. Given a cofiber sequence
![]() $E_1 \to E_2 \to E_3$
, if the canonical resolution converges for any two of the three terms, then it converges for the third. This holds because all the functors involved are stable.
$E_1 \to E_2 \to E_3$
, if the canonical resolution converges for any two of the three terms, then it converges for the third. This holds because all the functors involved are stable.
The following result clearly holds in much greater generality, but for simplicity we state it in our restricted context:
Lemma 4.13. Set
 $E \in \mathcal {SH}^{S^1}\!(k)$
and suppose we are given a tower
$E \in \mathcal {SH}^{S^1}\!(k)$
and suppose we are given a tower
and a sequence
![]() $n_i \in \mathbb {Z}$
such that
$n_i \in \mathbb {Z}$
such that
-
(1)
 $\operatorname *{\mathrm {lim}}_i n_i = \infty $
,
$\operatorname *{\mathrm {lim}}_i n_i = \infty $
, -
(2)
 $E_i \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i}$
(for all i), and
$E_i \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i}$
(for all i), and -
(3) the canonical resolution converges for
 $cof(E_{i+1} \to E_i)$
(for all i).
$cof(E_{i+1} \to E_i)$
(for all i).
Then the canonical resolution converges for E.
Proof. Define an endofunctor F of
 $\mathcal {SH}^{S^1}\!(k)$
by
$\mathcal {SH}^{S^1}\!(k)$
by
![]() $F(X) = fib\left (X \to X^{\wedge }\right )$
. By construction, this is a stable functor such that
$F(X) = fib\left (X \to X^{\wedge }\right )$
. By construction, this is a stable functor such that
![]() $F(X) \simeq 0$
if and only if the canonical resolution converges for X. Since
$F(X) \simeq 0$
if and only if the canonical resolution converges for X. Since
![]() $F(cof(E_{i+1} \to E_i)) \simeq 0$
for all i, we find that the tower
$F(cof(E_{i+1} \to E_i)) \simeq 0$
for all i, we find that the tower
is constant. In order to prove that
![]() $F(E) = 0$
, it thus suffices to show that
$F(E) = 0$
, it thus suffices to show that
![]() $\operatorname *{\mathrm {lim}}_i F(E_i) \simeq 0$
. Commuting the limits, we find that
$\operatorname *{\mathrm {lim}}_i F(E_i) \simeq 0$
. Commuting the limits, we find that
 $$ \begin{align*} \operatorname*{\mathrm{lim}}_i F(E_i) \simeq \operatorname*{\mathrm{lim}}_{i \ge 0, n \in \Delta} fib\left(E_i \to (\omega^\infty \sigma^\infty)^{\circ (n+1)} E_i\right) \simeq \operatorname*{\mathrm{lim}}_{n \in \Delta} \operatorname*{\mathrm{lim}}_i fib\left(E_i \to (\omega^\infty \sigma^\infty)^{\circ (n+1)} E_i\right); \end{align*} $$
$$ \begin{align*} \operatorname*{\mathrm{lim}}_i F(E_i) \simeq \operatorname*{\mathrm{lim}}_{i \ge 0, n \in \Delta} fib\left(E_i \to (\omega^\infty \sigma^\infty)^{\circ (n+1)} E_i\right) \simeq \operatorname*{\mathrm{lim}}_{n \in \Delta} \operatorname*{\mathrm{lim}}_i fib\left(E_i \to (\omega^\infty \sigma^\infty)^{\circ (n+1)} E_i\right); \end{align*} $$
it thus suffices to show that the inner limit over i vanishes. Since
![]() $\sigma ^\infty $
and
$\sigma ^\infty $
and
![]() $\omega ^\infty $
are both right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1,2)], we have
$\omega ^\infty $
are both right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1,2)], we have
 $fib(\ldots ) \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i - 1}$
, and hence it is enough to show that if
$fib(\ldots ) \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i - 1}$
, and hence it is enough to show that if
![]() $X_i$
is a sequence of spectra with
$X_i$
is a sequence of spectra with
 $X_i \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i}$
then
$X_i \in \mathcal {SH}^{S^1}\!(k)_{\ge n_i}$
then
![]() $\operatorname *{\mathrm {lim}}_i X_i \simeq 0$
. Since
$\operatorname *{\mathrm {lim}}_i X_i \simeq 0$
. Since
 $\mathcal {SH}^{S^1}\!(k)$
is generated as a localizing subcategory by objects of the form
$\mathcal {SH}^{S^1}\!(k)$
is generated as a localizing subcategory by objects of the form
![]() $\Sigma ^\infty _{S^1} U_+$
for
$\Sigma ^\infty _{S^1} U_+$
for
![]() $U \in {\mathrm {S}\mathrm {m}}_k$
, considering the Milnor exact sequence [Reference Goerss and Jardine7, Proposition VI.2.15] it suffices to show that if
$U \in {\mathrm {S}\mathrm {m}}_k$
, considering the Milnor exact sequence [Reference Goerss and Jardine7, Proposition VI.2.15] it suffices to show that if
![]() $n> \dim U$
, then
$n> \dim U$
, then
 $\left [\Sigma ^\infty _{S^1} U_+, \mathcal {SH}^{S^1}\!(k)_{\ge n}\right ] = 0$
. This follows from the descent spectral sequence.
$\left [\Sigma ^\infty _{S^1} U_+, \mathcal {SH}^{S^1}\!(k)_{\ge n}\right ] = 0$
. This follows from the descent spectral sequence.
Theorem 4.14. Let k be a perfect field such that
![]() $T_d(k)$
holds.
$T_d(k)$
holds.
-
(1) The canonical resolution converges for all
 $E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(d)$
.
$E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(d)$
. -
(2) Suppose in addition that
 $S_j(k)$
holds for all
$S_j(k)$
holds for all
 $1 \le j < d$
. Then the canonical resolution converges for all
$1 \le j < d$
. Then the canonical resolution converges for all
 $E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(1)$
.
$E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal {SH}^{S^1}\!(k)(1)$
.
Proof. (1) Write
 $\tau _{\ge i}^d$
for the truncation in the t-structure on
$\tau _{\ge i}^d$
for the truncation in the t-structure on
 $\mathcal {SH}^{S^1}\!(k)(d)$
. We have
$\mathcal {SH}^{S^1}\!(k)(d)$
. We have
 $E \in \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)]. Apply Lemma 4.13 with
$E \in \mathcal {SH}^{S^1}\!(k)(d)_{\ge 0}$
[Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(3)]. Apply Lemma 4.13 with
 $E_i = \tau _{\ge i}^d E$
and
$E_i = \tau _{\ge i}^d E$
and
![]() $n_i = i$
; assumption (i) is clear, and (ii) holds by [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1)]. For (iii), it suffices by Example 4.11 to show that
$n_i = i$
; assumption (i) is clear, and (ii) holds by [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2(1)]. For (iii), it suffices by Example 4.11 to show that
![]() $\pi _i^d E$
is in the essential image of
$\pi _i^d E$
is in the essential image of
![]() $\omega ^\infty $
. This follows from Theorem 4.6.
$\omega ^\infty $
. This follows from Theorem 4.6.
(2) By Example 4.12, part (1) of the theorem, and induction, it suffices to show that the canonical resolution converges for
![]() $s_j E$
, for
$s_j E$
, for
![]() $1 \le j < d$
. Since
$1 \le j < d$
. Since
 $f_j: \mathcal {SH}^{S^1}\!(k) \to \mathcal {SH}^{S^1}\!(k)$
is right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2], we have
$f_j: \mathcal {SH}^{S^1}\!(k) \to \mathcal {SH}^{S^1}\!(k)$
is right-t-exact [Reference Bosch, Lütkebohmert and Raynaud2, Lemma 6.2], we have
 $s_j E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
. Apply Lemma 4.13 with
$s_j E \in \mathcal {SH}^{S^1}\!(k)_{\ge 0}$
. Apply Lemma 4.13 with
 $E_i = f_j\left [\left (s_j E\right )_{\ge i}\right ]$
and
$E_i = f_j\left [\left (s_j E\right )_{\ge i}\right ]$
and
![]() $n_i = i$
. Assumption (i) is clear, (ii) holds by the right-t-exactness of
$n_i = i$
. Assumption (i) is clear, (ii) holds by the right-t-exactness of
![]() $f_j$
, and (iii) holds by the definition of
$f_j$
, and (iii) holds by the definition of
![]() $S_j(k)$
and Example 4.11.
$S_j(k)$
and Example 4.11.
Corollary 4.15.
-
(1) Suppose that
 $T_d(k)$
holds. Then is conservative.
$T_d(k)$
holds. Then is conservative. $$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal{SH}^{S^1}\!(k)(d) \to \mathcal{SH}(k) \end{align*} $$
$$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal{SH}^{S^1}\!(k)(d) \to \mathcal{SH}(k) \end{align*} $$
-
(2) Suppose that additionally
 $S_j(k)$
holds, for
$S_j(k)$
holds, for
 $1 \le j < d$
. Then is conservative.
$1 \le j < d$
. Then is conservative. $$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal{SH}^{S^1}\!(k)(1) \to \mathcal{SH}(k) \end{align*} $$
$$ \begin{align*} \sigma^\infty: \mathcal{SH}^{S^1}\!(k)_{\ge 0} \cap \mathcal{SH}^{S^1}\!(k)(1) \to \mathcal{SH}(k) \end{align*} $$
In particular, (1) holds for
![]() $d = 3$
if k is perfect, and (2) holds if
$d = 3$
if k is perfect, and (2) holds if
![]() $char(k) = 0$
.
$char(k) = 0$
.
Proof. Clearly the convergence of canonical resolutions implies conservativity (which is equivalent to detecting zero objects, by considering cofibers), so this is immediate from Theorem 4.14.
Acknowledgments
It is my pleasure to thank Maria Yakerson, Marc Levine, and Mike Hopkins for fruitful discussions about these problems.
I would also like to thank Marc Hoyois and Maria Yakerson for comments on a draft of this article.
The author declares no competing interests.