1. Introduction
Climate change poses major challenges that climate policy has not yet been able to address. In addition, technological solutions have not yet reached the scale needed to be sufficiently effective and to reduce polluting emissions to the extent required. Sustained and coordinated efforts by all stakeholders such as public and private sectors are needed to significantly reverse the trend.
This study develops a theoretical dynamic general equilibrium model to explore the interplay between public finance, public investment in adaptation infrastructure, and public support for private mitigation. The environmental tax will raise public revenues, but public adaptation and subsidies for private mitigation expenditure require revenue. We are interested in the issue of the efficient mix between adaptation and mitigation, which has been extensively analyzed in the literature, but also in the role of fiscal policy in this mix. Pollution taxation encourages the reduction of polluting emissions and provides public revenue. This revenue can be used to finance both mitigation and adaptation. In addition, while adaptation can have undesirable effects on the environment and increase pollution-related tax revenues, mitigation reduces pollution and tax revenues (cf. Enríquez-de-Salamanca et al. Reference Enríquez-de-Salamanca, Díaz-Sierra, Martín-Aranda and Santos2017). The fiscal dimension has been neglected in economic literature, with the exception of Barrage (Reference Barrage2020), Catalano et al. (Reference Catalano, Forni and Pezzolla2020a), and Habla and Roeder (Reference Habla and Roeder2017). In the latter, the mitigation policy consists of taxation and adaptation is a public expenditure while Catalano et al. (Reference Catalano, Forni and Pezzolla2020a) focus only on adaptation financing. We add to this literature by considering a mitigation sector financed by private expenditure in abatement activities (which is different from the pollution tax assumed in Habla and Roeder Reference Habla and Roeder2017). By contrast, adaptation is a public policy, comprising public investment in infrastructure such as dams, bridges and roads. We assume investment in adaptation infrastructure as a public decision, because these investments require good knowledge of the long term.
To analyze the interactions between environmental taxation, adaptation, and mitigation investments, this study considers an overlapping generations (OLG) model with an environmental externality. We extend the model developed by John and Pecchenino (Reference John and Pecchenino1994) to consider public adaptation and private mitigation. We study the interactions between private decisions regarding pollution mitigation and government intervention in adaptation. We focus on an economy in which households are involved in environmental abatement through a trade-off between consumption and mitigation alongside public adaptation to protect them from the consequences of pollution. Pollution emissions occur through consumption, which harms the welfare of future generations. Public expenditure on adaptation investments is financed by taxation, and debt financing is also considered. Fiscal policy has a twofold effect on households’ budget constraints through taxation for financing public adaptation and through subsidies for private mitigation. We show that adaptation and mitigation may be substitutes or complements depending on the level of economic development, but also on the level of mitigation subsidy. Finally, when the government is indebted, we show that financing public adaptation and/or subsidizing private mitigation through an increase in public debt could be beneficial for countries with a high capital stock, but is detrimental when its capital stock is too low.
Our study contributes to the literature in two ways. First, it is related to the literature on the intergenerational issues of environmental policies (e.g., Bovenberg and Heijdra Reference Bovenberg and Heijdra1998, Reference Bovenberg and Heijdra2002; Chiroleu-Assouline and Fodha Reference Chiroleu-Assouline and Fodha2006; Mariani et al. Reference Mariani, Pérez-Barahona and Raffin2010; Karp and Rezai Reference Karp and Rezai2014). In these studies, intergenerational conflicts arise because of the distributional effects of environmental policies on the welfare of current and future generations. In Habla and Roeder (Reference Habla and Roeder2017), climate policies have heterogeneous welfare consequences mainly through the impacts on the budget constraints of current and future generations. Fodha and Seegmuller (Reference Fodha and Seegmuller2012, Reference Fodha and Seegmuller2014) and Fodha et al. (Reference Fodha, Seegmuller and Yamagami2018) analyze debt financing schemes of mitigation. They show that a poverty trap may exist, but efficient environmental tax reform may be designed under specific conditions on abatement technologies and initial level of capital stock. In these studies, public and private actions to mitigate pollution rely on the same technologies; they are thus supposed to be perfectly substitutable. In our study, we add adaptation policies and consider a vulnerability function that translates pollution into welfare losses. We show that public and private decisions may also be complements.
Second, our study adds to the theoretical literature on mitigation and adaptation, which focuses on the conditions under which adaptation and mitigation are substitutes or complements. Ayong and Pommeret (Reference Ayong le Kama and Pommeret2017) consider a pollution threshold above which adaptation is no longer efficient. Bréchet et al. (Reference Bréchet, Hritonenko and Yatsenko2013) study optimal mitigation and adaptation investments at the macroeconomic level and show that the issue of substitutability between the two instruments depends on the stage of development. Ingham et al. (Reference Ingham, Ma and Ulph2013) develop a range of economic models to explore the relationship between mitigation and adaptation. They show that mitigation and adaptation are substitutes in almost all economic models of climate change. However, they also find that complementarity is possible when adaptation costs depend on the level of mitigation. Schumacher (Reference Schumacher2019) assumes that mitigation is a public good, whereas adaptation is a private good, and concludes that mitigation must be preferred to adaptation. Regarding the public finance issue, the articles take into account the taxation of pollution to finance either adaptation expenditure (Barrage, Reference Barrage2020; Bachner et al. Reference Bachner, Bednar-Friedl and Knittel2019; Habla and Roeder Reference Habla and Roeder2017), or an abatement sector (Jondeau et al. Reference Jondeau, Levieuge, Sahuc and Vermandel2022). Barrage (Reference Barrage2020) shows that distortive taxation affects the efficiency of adaptation and increases the welfare costs of climate change. Conversely, Bachner et al. (Reference Bachner, Bednar-Friedl and Knittel2019) suggest that a well-designed adaptation policy has a positive effect on economic growth and welfare. Habla and Roeder (Reference Habla and Roeder2017) argue that the redistributive characteristics of the tax structure plays an important role for the acceptability of the adaptation policies. Finally, Jondeau et al. (Reference Jondeau, Levieuge, Sahuc and Vermandel2022) conclude that public subsidies to the abatement sector, when financed by pollution taxes, is an efficient policy. In our article, private mitigation and public adaptation decisions are considered simultaneously. This is important because the two investments interact with each other, affecting pollution emissions and public budget. We show that the financing scheme is an important argument in the debate on the optimal mix of adaptation and mitigation.
The remainder of this paper is organized as follows. Section 2 describes the OLG model. Section 3 defines the intertemporal equilibria and examines the stability of the steady states. Section 4 presents the welfare analysis. Section 5 considers three extensions: (i) adaptation investment proportional to pollution flow, (ii) adaptation financed by public debt, and (iii) mitigation by government and adaptation by private agents. The final section concludes.
2. An OLG model
We consider an OLG model with three agents: individuals (young and old), firms, and a government. In a model à la John and Pecchenino (Reference John and Pecchenino1994), we extend the results of Fodha and Seegmuller (Reference Fodha and Seegmuller2012) by considering public adaptation alongside private mitigation.
2.1. The environment
We suppose that a stock of pollution,
![]() $E_{t+1}$
, is increased by consumption,
$E_{t+1}$
, is increased by consumption,
![]() $c_t$
, but reduced by mitigation,
$c_t$
, but reduced by mitigation,
![]() $m_t$
:
$m_t$
:
where
![]() $\delta _E\in (0,1)$
measures a natural rate of pollution absorption.
$\delta _E\in (0,1)$
measures a natural rate of pollution absorption.
![]() $\epsilon,\gamma \gt 0$
represent the rate of pollution from consumption and the efficiency of pollution abatement from mitigation, respectively.Footnote
1
$\epsilon,\gamma \gt 0$
represent the rate of pollution from consumption and the efficiency of pollution abatement from mitigation, respectively.Footnote
1
Pollution stock is a source of damage, resulting in climate change, frequent flooding, rising sea levels, and an increase in infectious diseases. However, damage can be alleviated through adaptation
![]() $H_{t+1}$
, such as dams, sea- or river-side banks, and medical knowledge. This could be public infrastructure or human capital. The adaptation stock is increased by public investment
$H_{t+1}$
, such as dams, sea- or river-side banks, and medical knowledge. This could be public infrastructure or human capital. The adaptation stock is increased by public investment
![]() $h_t$
:
$h_t$
:
where
![]() $\bar {H}\gt 0$
is a basic (natural) adaptation level that nature provides and
$\bar {H}\gt 0$
is a basic (natural) adaptation level that nature provides and
![]() $\delta _H\in (0,1)$
denotes the rate of adaptation stock depreciation. Natural adaptation (
$\delta _H\in (0,1)$
denotes the rate of adaptation stock depreciation. Natural adaptation (
![]() $\bar {H}$
) is a long-term exogenous adaptation capacity that can be interpreted as the natural capacity of an ecosystem to protect humans. The higher the
$\bar {H}$
) is a long-term exogenous adaptation capacity that can be interpreted as the natural capacity of an ecosystem to protect humans. The higher the
![]() $\bar {H}$
, the more resistant the human being is to the hazards of nature, reflecting the low impact of pollution on well-being.
$\bar {H}$
, the more resistant the human being is to the hazards of nature, reflecting the low impact of pollution on well-being.
![]() $\bar {H}$
represents a natural long-term equilibrium (water, air, biodiversity, etc.) in the absence of any human activity.Footnote
2
$\bar {H}$
represents a natural long-term equilibrium (water, air, biodiversity, etc.) in the absence of any human activity.Footnote
2
Adaptation and mitigation investments play distinct roles. On the one hand, adaptation
![]() $h$
is an investment that increases a stock of public good,
$h$
is an investment that increases a stock of public good,
![]() $H$
, financed by the government. On the other hand, mitigation
$H$
, financed by the government. On the other hand, mitigation
![]() $m$
is a privately provided good that decreases the pollution stock
$m$
is a privately provided good that decreases the pollution stock
![]() $E$
. With regard to climate change,
$E$
. With regard to climate change,
![]() $h$
is investment in infrastructure, education and R&D.
$h$
is investment in infrastructure, education and R&D.
![]() $m$
is investment in GHG emission abatement services, such as CCS or renewable energy, and in the insulation of buildings.
$m$
is investment in GHG emission abatement services, such as CCS or renewable energy, and in the insulation of buildings.
2.2. Households
We consider an OLG model with 2-period-lived agents. The population size of each generation is assumed constant and normalized to unity. An individual born at time
![]() $t$
inelastically supplies one unit of labor when young, shares her wage between savings and investment in mitigation,
$t$
inelastically supplies one unit of labor when young, shares her wage between savings and investment in mitigation,
![]() $m_{t}$
, and consumes when old,
$m_{t}$
, and consumes when old,
![]() $c_{t+1}$
. In addition, she suffers from a stock of pollution when old,
$c_{t+1}$
. In addition, she suffers from a stock of pollution when old,
![]() $E_{t+1}$
, through climate change, sea level rise, or infectious diseases. However, vulnerability to environmental degradation is alleviated by a stock of adaptation,
$E_{t+1}$
, through climate change, sea level rise, or infectious diseases. However, vulnerability to environmental degradation is alleviated by a stock of adaptation,
![]() $H_{t+1}$
.
$H_{t+1}$
.
We define a sub-utility function,
![]() $q_{t+1}=Q(E_{t+1},H_{t+1})$
, which measures the quality of life related to the pollution stock. This quality is assumed to decrease with the pollution stock but increases with the adaptation stock. Together with consumption, we suppose that the utility of an individual born at time
$q_{t+1}=Q(E_{t+1},H_{t+1})$
, which measures the quality of life related to the pollution stock. This quality is assumed to decrease with the pollution stock but increases with the adaptation stock. Together with consumption, we suppose that the utility of an individual born at time
![]() $t$
is
$t$
is
where
![]() $\beta \in (0,1)$
is a preference parameter for consumption,
$\beta \in (0,1)$
is a preference parameter for consumption,
![]() $\phi \gt 0$
measures the sensitivity of quality of life to the pollution stock, and
$\phi \gt 0$
measures the sensitivity of quality of life to the pollution stock, and
![]() $\mu \gt 0$
is an efficiency parameter of the adaptation stock.
$\mu \gt 0$
is an efficiency parameter of the adaptation stock.
![]() $\phi$
can be interpreted as a parameter that determines the willingness to pay to reduce pollution or as a factor determining the share of mitigation expenditure in household income.
$\phi$
can be interpreted as a parameter that determines the willingness to pay to reduce pollution or as a factor determining the share of mitigation expenditure in household income.
![]() $\mu$
can be interpreted as a vulnerability parameter, and
$\mu$
can be interpreted as a vulnerability parameter, and
![]() $H^\mu$
represents the environmental resilience or the efficiency of adaptation to protect people from adverse climate change effects.
$H^\mu$
represents the environmental resilience or the efficiency of adaptation to protect people from adverse climate change effects.
An individual born at time
![]() $t$
earns disposable income when young as the difference between wage
$t$
earns disposable income when young as the difference between wage
![]() $w_t$
, and lump-sum tax
$w_t$
, and lump-sum tax
![]() $T_t$
. She allocates this to mitigation
$T_t$
. She allocates this to mitigation
![]() $m_t$
and savings
$m_t$
and savings
![]() $s_t$
. When old, the agent consumes
$s_t$
. When old, the agent consumes
![]() $(c_{t+1})$
her remunerated savings, with
$(c_{t+1})$
her remunerated savings, with
![]() $R_{t+1}$
the real interest rate. The mitigation subsidy is
$R_{t+1}$
the real interest rate. The mitigation subsidy is
![]() $v$
, and the rate of consumption tax is
$v$
, and the rate of consumption tax is
![]() $\tau _c$
. Thus, the individual maximizes (3) subject to (4) and (1) and the following budget constraints:
$\tau _c$
. Thus, the individual maximizes (3) subject to (4) and (1) and the following budget constraints:
Households have to pay a tax
![]() $\tau ^c$
on polluting consumption (i.e., Pigovian tax). Their life-cycle income is also affected by a transfer
$\tau ^c$
on polluting consumption (i.e., Pigovian tax). Their life-cycle income is also affected by a transfer
![]() $T_t$
(positive or negative) that balances the government budget. Households bear double taxation over their lifecycles (
$T_t$
(positive or negative) that balances the government budget. Households bear double taxation over their lifecycles (
![]() $T$
and
$T$
and
![]() $\tau _c$
). These two instruments are complementary, and allow us to define a complete system of instruments to decentralize the social optimum. The lump-sum tax has an impact on the level of life-cycle net income (scale effect), while the tax on consumption influences the pollution externalities from consumption.
$\tau _c$
). These two instruments are complementary, and allow us to define a complete system of instruments to decentralize the social optimum. The lump-sum tax has an impact on the level of life-cycle net income (scale effect), while the tax on consumption influences the pollution externalities from consumption.
Combining (5) and (6) leads to the intertemporal budget constraint.
![]() $H_{t+1}$
in (2) is given for agents. We derive the demand for mitigation when young, and consumption when old.
$H_{t+1}$
in (2) is given for agents. We derive the demand for mitigation when young, and consumption when old.
The consequences of mitigation on the pollution stock are twofold. First, mitigation
![]() $m_t$
directly decreases the pollution stock
$m_t$
directly decreases the pollution stock
![]() $E_{t+1}$
. Second, higher investment in mitigation implies a decrease in individual savings and lower consumption in period
$E_{t+1}$
. Second, higher investment in mitigation implies a decrease in individual savings and lower consumption in period
![]() $t+1$
. As adaptation is given, the vulnerability indicator does not influence agents’ trade-offs. Public adaptation has no direct consequence for the mitigation private decision.
$t+1$
. As adaptation is given, the vulnerability indicator does not influence agents’ trade-offs. Public adaptation has no direct consequence for the mitigation private decision.
2.3. Firms
The firm produces an aggregate output using a Cobb–Douglas technology with capital stock
![]() $K_t$
and labor
$K_t$
and labor
![]() $L_t$
:
$L_t$
:
![]() $Y_t =AK_t^\alpha L_t^{1-\alpha }$
with
$Y_t =AK_t^\alpha L_t^{1-\alpha }$
with
![]() $A \gt 0$
and
$A \gt 0$
and
![]() $\alpha \in (0,1)$
. Labor input equals one. We rewrite the production function as per capita
$\alpha \in (0,1)$
. Labor input equals one. We rewrite the production function as per capita
![]() $y_t = Ak_t$
, where
$y_t = Ak_t$
, where
![]() $y_t$
and
$y_t$
and
![]() $k_t$
are the output and capital stock per young capita, respectively. The tax rate on production is
$k_t$
are the output and capital stock per young capita, respectively. The tax rate on production is
![]() $\tau ^y$
. This will affect the dynamics of capital accumulation.
$\tau ^y$
. This will affect the dynamics of capital accumulation.
The first-order conditions of profit maximization are given by
We assume a full depreciation of capital in one period.
2.4. Government
The government’s budget is balanced at each period:
We first assume that investment in adaptation is constant over time,
![]() $h_t = \bar {h}$
,
$h_t = \bar {h}$
,
![]() $\forall t$
. This investment is an environmental policy instrument. We therefore assume that adaptation is a choice made by independent local authorities and taken as given by central authorities in charge of taxation. We will relax this assumption later.
$\forall t$
. This investment is an environmental policy instrument. We therefore assume that adaptation is a choice made by independent local authorities and taken as given by central authorities in charge of taxation. We will relax this assumption later.
The distributive effects of adaptation and mitigation differ. The costs of environmental policies at time
![]() $t$
(investment in adaptation and mitigation subsidies) are borne by all agents living at time
$t$
(investment in adaptation and mitigation subsidies) are borne by all agents living at time
![]() $t$
including old agents and firms, whereas the benefits will take place at time
$t$
including old agents and firms, whereas the benefits will take place at time
![]() $t + 1$
. Mitigation is privately financed by the young at time
$t + 1$
. Mitigation is privately financed by the young at time
![]() $t$
for their own benefit when old at time
$t$
for their own benefit when old at time
![]() $t + 1$
.
$t + 1$
.
3. Intertemporal equilibrium
Capital stock equals total savings:
![]() $k_{t+1} = s_t$
. By substituting (6) and (8), we obtain
$k_{t+1} = s_t$
. By substituting (6) and (8), we obtain
With (1), the dynamics of capital stock in (12) is rearranged as
We also rewrite
![]() $m_t$
in (7) with (10) – (12) and
$m_t$
in (7) with (10) – (12) and
![]() $c_t$
in (8) with (9) and (12):
$c_t$
in (8) with (9) and (12):
Substituting (14) and (15) into (13) yields the following dynamics of capital stock:
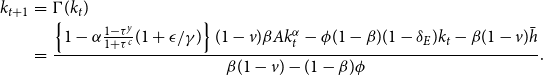 \begin{eqnarray} k_{t+1}&=&\Gamma (k_t)\nonumber \\ &=&\frac { \left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}(1-v)\beta Ak_t^\alpha -\phi (1-\beta)(1-\delta _E) k_t-\beta (1-v)\bar {h}}{\beta (1-v)-(1-\beta)\phi }. \end{eqnarray}
\begin{eqnarray} k_{t+1}&=&\Gamma (k_t)\nonumber \\ &=&\frac { \left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}(1-v)\beta Ak_t^\alpha -\phi (1-\beta)(1-\delta _E) k_t-\beta (1-v)\bar {h}}{\beta (1-v)-(1-\beta)\phi }. \end{eqnarray}
3.1. Laissez-faire equilibrium
We first consider the laissez-faire case (
![]() $\tau ^c =\tau ^y = v = \bar {h} = 0$
). Dynamics defined in eq. (16) reduces to
$\tau ^c =\tau ^y = v = \bar {h} = 0$
). Dynamics defined in eq. (16) reduces to
We make the following assumptions to obtain the nontrivial steady state in the laissez-faire economy:
Assumption 1.
(a)
![]() $\frac {\beta }{1-\beta }\gt \phi$
and (b)
$\frac {\beta }{1-\beta }\gt \phi$
and (b)
![]() $\frac {\gamma }{\epsilon } \gt \frac {\alpha }{1-\alpha }$
.
$\frac {\gamma }{\epsilon } \gt \frac {\alpha }{1-\alpha }$
.
Assumption1 (a) compares the sensitivity of the quality of life to pollution (
![]() $\phi$
) to the sensitivity of utility to consumption (
$\phi$
) to the sensitivity of utility to consumption (
![]() $\beta$
). Assumption1 (b) is standard and not too restrictive. This implies that
$\beta$
). Assumption1 (b) is standard and not too restrictive. This implies that
![]() $\gamma (1-\alpha)Ak^\alpha \gt \epsilon \alpha Ak^\alpha$
. In the absence of taxes, we have
$\gamma (1-\alpha)Ak^\alpha \gt \epsilon \alpha Ak^\alpha$
. In the absence of taxes, we have
![]() $c = Rs = Rk = \alpha Ak^\alpha$
and
$c = Rs = Rk = \alpha Ak^\alpha$
and
![]() $w = (1 -\alpha) Ak^\alpha$
. Thus, the assumption is rewritten as
$w = (1 -\alpha) Ak^\alpha$
. Thus, the assumption is rewritten as
![]() $\gamma (1 -\alpha)w \gt \epsilon \alpha c$
, meaning that if an agent uses all her wages for mitigation (
$\gamma (1 -\alpha)w \gt \epsilon \alpha c$
, meaning that if an agent uses all her wages for mitigation (
![]() $m = w$
), it efficiently fights the flow of pollution from consumption, and then ensures that the flow of net pollution is negative.
$m = w$
), it efficiently fights the flow of pollution from consumption, and then ensures that the flow of net pollution is negative.
Consequently, we have a positive denominator in (17) from assumption1 (a). Additionally,
![]() $\Gamma _0(0)=0$
,
$\Gamma _0(0)=0$
,
![]() $\lim _{k_t\rightarrow 0} \Gamma _0^{\prime} (k_t)=+ \infty$
, and
$\lim _{k_t\rightarrow 0} \Gamma _0^{\prime} (k_t)=+ \infty$
, and
![]() $\lim _{k_t\rightarrow +\infty } \Gamma _0^{\prime} (k_t)\lt 0$
.Footnote
3
Therefore, we obtain an inverted U-shaped curve in the dynamics of
$\lim _{k_t\rightarrow +\infty } \Gamma _0^{\prime} (k_t)\lt 0$
.Footnote
3
Therefore, we obtain an inverted U-shaped curve in the dynamics of
![]() $k$
with an intercept at
$k$
with an intercept at
![]() $k_{t+1}=0$
. Then, two steady states exist, such that
$k_{t+1}=0$
. Then, two steady states exist, such that
![]() $k=\Gamma _0(k)$
. Letting
$k=\Gamma _0(k)$
. Letting
![]() $k_{0,ss}^1$
and
$k_{0,ss}^1$
and
![]() $k_{0,ss}^2$
be the capital stock levels at steady state, we have
$k_{0,ss}^2$
be the capital stock levels at steady state, we have
To examine the stability of each steady state, we define
![]() $\overline {k_0}$
as the capital stock that satisfies
$\overline {k_0}$
as the capital stock that satisfies
![]() $\Gamma _0^{\prime}(\overline {k_0})=0$
and
$\Gamma _0^{\prime}(\overline {k_0})=0$
and
![]() $\underline {k_0}$
as the stock satisfying
$\underline {k_0}$
as the stock satisfying
![]() $\Gamma _0^{\prime}(\underline {k_0})=-1$
. These are rewritten as
$\Gamma _0^{\prime}(\underline {k_0})=-1$
. These are rewritten as
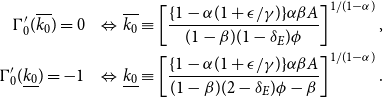 \begin{eqnarray*} \Gamma _0^{\prime}(\overline {k_0})=0\;\;\; & \Leftrightarrow & \overline {k_0}\equiv \left [ \frac {\{ 1-\alpha (1+\epsilon /\gamma) \}\alpha \beta A}{(1-\beta)(1-\delta _E)\phi } \right]^{1/(1-\alpha)}, \\ \Gamma _0^{\prime}(\underline {k_0})=-1\;\;\; & \Leftrightarrow & \underline {k_0}\equiv \left [ \frac {\{ 1-\alpha (1+\epsilon /\gamma) \}\alpha \beta A}{(1-\beta)(2-\delta _E)\phi -\beta } \right]^{1/(1-\alpha)}. \end{eqnarray*}
\begin{eqnarray*} \Gamma _0^{\prime}(\overline {k_0})=0\;\;\; & \Leftrightarrow & \overline {k_0}\equiv \left [ \frac {\{ 1-\alpha (1+\epsilon /\gamma) \}\alpha \beta A}{(1-\beta)(1-\delta _E)\phi } \right]^{1/(1-\alpha)}, \\ \Gamma _0^{\prime}(\underline {k_0})=-1\;\;\; & \Leftrightarrow & \underline {k_0}\equiv \left [ \frac {\{ 1-\alpha (1+\epsilon /\gamma) \}\alpha \beta A}{(1-\beta)(2-\delta _E)\phi -\beta } \right]^{1/(1-\alpha)}. \end{eqnarray*}
From Assumption1, we obtain
![]() $k_{0,ss}^1\lt \overline {k_0}\lt \underline {k_0}$
. Then, we present three cases of dynamics: (i)
$k_{0,ss}^1\lt \overline {k_0}\lt \underline {k_0}$
. Then, we present three cases of dynamics: (i)
![]() $k_{0,ss}^1\lt \overline {k_0}\lt \underline {k_0}\le k_{0,ss}^2$
; (ii)
$k_{0,ss}^1\lt \overline {k_0}\lt \underline {k_0}\le k_{0,ss}^2$
; (ii)
![]() $k_{0,ss}^1\lt \overline {k_0}\lt k_{0,ss}^2\lt \underline {k_0}$
; and (iii)
$k_{0,ss}^1\lt \overline {k_0}\lt k_{0,ss}^2\lt \underline {k_0}$
; and (iii)
![]() $k_{0,ss}^1\lt k_{0,ss}^2\le \overline {k_0}\lt \underline {k_0}$
, which are depicted in Figure 1. As shown in Figure 1, the positive steady state
$k_{0,ss}^1\lt k_{0,ss}^2\le \overline {k_0}\lt \underline {k_0}$
, which are depicted in Figure 1. As shown in Figure 1, the positive steady state
![]() $k_{0,ss}^2$
is unstable in case (i) and stable in cases (ii) and (iii).
$k_{0,ss}^2$
is unstable in case (i) and stable in cases (ii) and (iii).
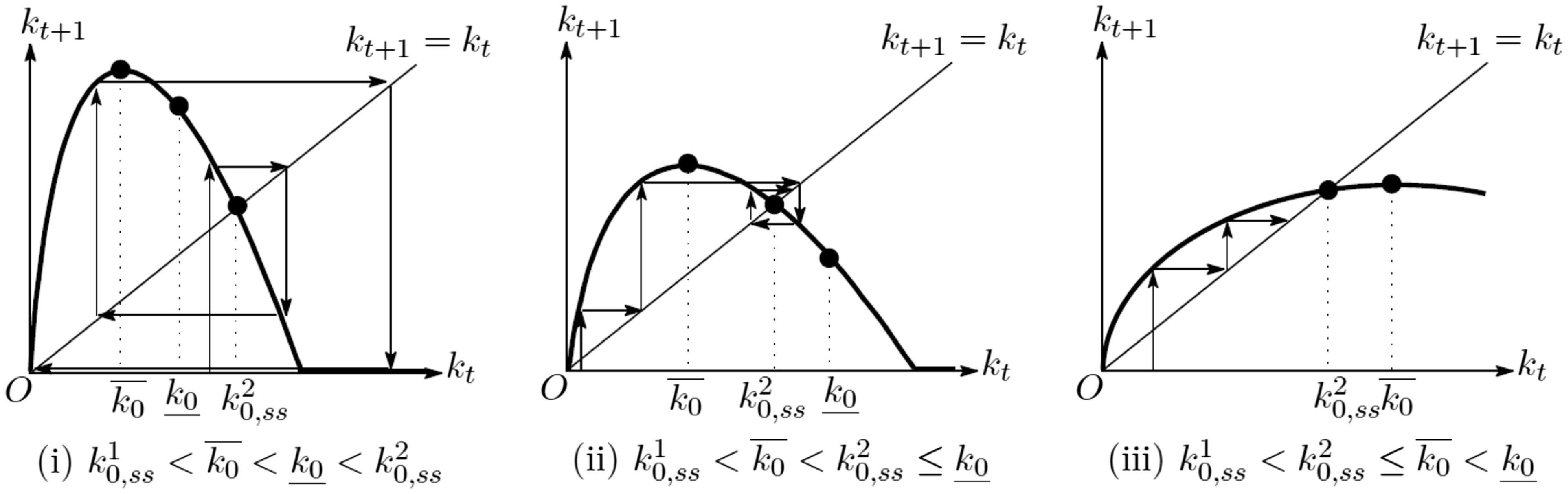
Figure 1. Capital stock dynamics in the laissez-faire economy.
We add the following assumption to ensure the existence of a nontrivial stable steady state in the laissez-faire cases, such as in cases (ii) and (iii). This is achieved by assuming
![]() $k_{0,ss}^2\lt \underline {k_0}$
, which is rearranged as follows:
$k_{0,ss}^2\lt \underline {k_0}$
, which is rearranged as follows:
Assumption 2.
![]() $1\gt \beta \gt \frac {\phi \{ 2-\delta _E(1-\alpha) \}}{(1+\alpha)+\phi \{ 2-\delta _E(1-\alpha) \}}\gt 0.$
$1\gt \beta \gt \frac {\phi \{ 2-\delta _E(1-\alpha) \}}{(1+\alpha)+\phi \{ 2-\delta _E(1-\alpha) \}}\gt 0.$
This assumption also implies that utility is sufficiently sensitive to consumption.
3.2. Steady states with environmental policies
While holding Assumptions1 and 2, we study the dynamics of
![]() $k$
with policies, as in (13). We define
$k$
with policies, as in (13). We define
![]() $k_{ss}$
as the capital stock per young person if the steady state is unique, whereas
$k_{ss}$
as the capital stock per young person if the steady state is unique, whereas
![]() $k_{ss}^i$
with
$k_{ss}^i$
with
![]() $i=\{1,2,\cdots,n\}$
are those with
$i=\{1,2,\cdots,n\}$
are those with
![]() $k^i_{ss}\lt k_{ss}^j$
for
$k^i_{ss}\lt k_{ss}^j$
for
![]() $i\lt j$
if there are multiple steady states.
$i\lt j$
if there are multiple steady states.
Let us examine the steady-state capital stock. For this purpose, we define
![]() $\overline {k}$
,
$\overline {k}$
,
![]() $\underline {k}$
, and
$\underline {k}$
, and
![]() $\hat {k}$
that satisfy
$\hat {k}$
that satisfy
![]() $\Gamma ^{\prime}(\overline {k})=0$
,
$\Gamma ^{\prime}(\overline {k})=0$
,
![]() $\Gamma ^{\prime}(\underline {k})=-1$
,
$\Gamma ^{\prime}(\underline {k})=-1$
,
![]() $\Gamma ^{\prime}(\hat {k})=1$
, respectively.
$\Gamma ^{\prime}(\hat {k})=1$
, respectively.
 \begin{eqnarray} \Gamma ^{\prime}(\overline {k})=0\;\;\; & \Leftrightarrow & \overline {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)}\right]^{1/(1-\alpha)},\qquad\,\, \end{eqnarray}
\begin{eqnarray} \Gamma ^{\prime}(\overline {k})=0\;\;\; & \Leftrightarrow & \overline {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)}\right]^{1/(1-\alpha)},\qquad\,\, \end{eqnarray}
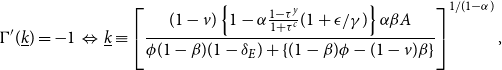 \begin{eqnarray} \Gamma ^{\prime}(\underline {k})=-1 & \Leftrightarrow & \underline {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)+\{(1-\beta)\phi -(1-v)\beta \}}\right]^{1/(1-\alpha)}, \end{eqnarray}
\begin{eqnarray} \Gamma ^{\prime}(\underline {k})=-1 & \Leftrightarrow & \underline {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)+\{(1-\beta)\phi -(1-v)\beta \}}\right]^{1/(1-\alpha)}, \end{eqnarray}
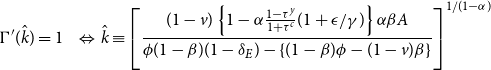 \begin{eqnarray} \Gamma ^{\prime}(\hat {k})=1 \;\;\; & \Leftrightarrow & \hat {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)-\{(1-\beta)\phi -(1-v)\beta \}}\right]^{1/(1-\alpha)}\,\,\, \end{eqnarray}
\begin{eqnarray} \Gamma ^{\prime}(\hat {k})=1 \;\;\; & \Leftrightarrow & \hat {k}\equiv \left [ \frac {(1-v)\left \{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A}{\phi (1-\beta)(1-\delta _E)-\{(1-\beta)\phi -(1-v)\beta \}}\right]^{1/(1-\alpha)}\,\,\, \end{eqnarray}
We define two values for the mitigation subsidy,
![]() $\underline {v}$
and
$\underline {v}$
and
![]() $\bar {v}$
, and summarize the existence and stability of the steady states as follows:
$\bar {v}$
, and summarize the existence and stability of the steady states as follows:
Note that
![]() $\bar {v}\gt \underline {v}$
because
$\bar {v}\gt \underline {v}$
because
![]() $\delta _E\in (0,1)$
.
$\delta _E\in (0,1)$
.
Additionally, from (16), we assume the following to exclude extreme cases:
Assumption 3.
![]() $(1-\beta)\phi -(1-v)\beta \neq 0 \Leftrightarrow v\neq \underline {v}.$
$(1-\beta)\phi -(1-v)\beta \neq 0 \Leftrightarrow v\neq \underline {v}.$
Assuming that the subsidy rate is sufficiently high or low, we can characterize the steady-state equilibrium conditions. This highlights the importance of environmental policy tools. The level of mitigation subsidy determines the properties of the steady-state equilibrium and will also help determine the consequences of environmental tax and public finance reforms.
PROPOSITION 1. Under Assumptions1, 2, and 3, the steady-state equilibria are characterized by the following nine cases.
-
(i) There is a unique steady state,
 $k_{ss}\gt 0$
, if
$k_{ss}\gt 0$
, if
 $\Gamma (\overline {k})\le \overline {k}$
and
$\Gamma (\overline {k})\le \overline {k}$
and
 $v\ge \bar {v}$
. Then, the steady state is stable if
$v\ge \bar {v}$
. Then, the steady state is stable if
 $k_{ss}\in (\underline {k},\overline {k})$
and unstable if
$k_{ss}\in (\underline {k},\overline {k})$
and unstable if
 $k_{ss}\le \underline {k}$
.
$k_{ss}\le \underline {k}$
. -
(ii) There exist two steady states,
 $k_{ss}^1$
and
$k_{ss}^1$
and
 $k_{ss}^2$
, such that
$k_{ss}^2$
, such that
 $0\lt k_{ss}^1\lt \overline {k}\lt k_{ss}^2$
if
$0\lt k_{ss}^1\lt \overline {k}\lt k_{ss}^2$
if
 $\Gamma (\overline {k})\le \overline {k}$
and
$\Gamma (\overline {k})\le \overline {k}$
and
 $\underline {v}\lt v\le \bar {v}$
. Then,
$\underline {v}\lt v\le \bar {v}$
. Then,
 $k_{ss}^2$
is unstable.
$k_{ss}^2$
is unstable.
 $k_{ss}^1$
is stable if
$k_{ss}^1$
is stable if
 $k_{ss}^1\in (\underline {k},\overline {k})$
and unstable if
$k_{ss}^1\in (\underline {k},\overline {k})$
and unstable if
 $k_{ss}^1\le \underline {k}$
.
$k_{ss}^1\le \underline {k}$
. -
(iii) There is a unique steady state,
 $k_{ss}$
, which is strictly greater than
$k_{ss}$
, which is strictly greater than
 $\overline {k}$
, if
$\overline {k}$
, if
 $\Gamma (\overline {k})\gt \overline {k}$
and
$\Gamma (\overline {k})\gt \overline {k}$
and
 $v\ge \bar {v}$
. Then, the steady state is stable.
$v\ge \bar {v}$
. Then, the steady state is stable.
-
(iv) There exist two steady states,
 $k_{ss}^1$
and
$k_{ss}^1$
and
 $k_{ss}^2$
, such that
$k_{ss}^2$
, such that
 $0\lt k_{ss}^1\lt \overline {k}\lt k_{ss}^2$
if
$0\lt k_{ss}^1\lt \overline {k}\lt k_{ss}^2$
if
 $\Gamma (\overline {k})\gt \overline {k}$
,
$\Gamma (\overline {k})\gt \overline {k}$
,
 $\underline {v}\lt v\lt \bar {v}$
, and
$\underline {v}\lt v\lt \bar {v}$
, and
 $\Gamma (\hat {k})\lt \hat {k}$
. Then,
$\Gamma (\hat {k})\lt \hat {k}$
. Then,
 $k_{ss}^1$
is stable and
$k_{ss}^1$
is stable and
 $k_{ss}^2$
is unstable.
$k_{ss}^2$
is unstable.
-
(v) There is a unique steady state,
 $k_{ss}\gt 0$
, if
$k_{ss}\gt 0$
, if
 $\Gamma (\overline {k})\gt \overline {k}$
,
$\Gamma (\overline {k})\gt \overline {k}$
,
 $\underline {v}\lt v\lt \bar {v}$
, and
$\underline {v}\lt v\lt \bar {v}$
, and
 $\Gamma (\hat {k})=\hat {k}$
. Then, the steady state,
$\Gamma (\hat {k})=\hat {k}$
. Then, the steady state,
 $k_{ss}$
, is unstable.
$k_{ss}$
, is unstable.
-
(vi) There is no steady state if
 $\Gamma (\overline {k})\gt \overline {k}$
,
$\Gamma (\overline {k})\gt \overline {k}$
,
 $\underline {v}\lt v\lt \bar {v}$
, and
$\underline {v}\lt v\lt \bar {v}$
, and
 $\Gamma (\hat {k})\gt \hat {k}$
.
$\Gamma (\hat {k})\gt \hat {k}$
. -
(vii) There is a unique steady state,
 $k_{ss}$
, if
$k_{ss}$
, if
 $\Gamma (\hat {k})\lt \hat {k}$
and
$\Gamma (\hat {k})\lt \hat {k}$
and
 $v\lt \underline {v}$
. Then, the steady state,
$v\lt \underline {v}$
. Then, the steady state,
 $k_{ss}$
, is zero and stable.
$k_{ss}$
, is zero and stable.
-
(viii) There exist two steady states,
 $k^1_{ss}$
and
$k^1_{ss}$
and
 $k^2_{ss}$
such that
$k^2_{ss}$
such that
 $k^1_{ss}\lt k^2_{ss}$
, if
$k^1_{ss}\lt k^2_{ss}$
, if
 $\Gamma (\hat {k})=\hat {k}$
and
$\Gamma (\hat {k})=\hat {k}$
and
 $v\lt \underline {v}$
. Then,
$v\lt \underline {v}$
. Then,
 $k^1_{ss}$
is zero and stable.
$k^1_{ss}$
is zero and stable.
 $k^2_{ss}$
is unstable.
$k^2_{ss}$
is unstable.
-
(ix) There are three steady states,
 $k^1_{ss}$
,
$k^1_{ss}$
,
 $k^2_{ss}$
, and
$k^2_{ss}$
, and
 $k^3_{ss}$
with
$k^3_{ss}$
with
 $k^1_{ss}\lt k^2_{ss}\lt k^3_{ss}$
, if
$k^1_{ss}\lt k^2_{ss}\lt k^3_{ss}$
, if
 $\Gamma (\hat {k})\gt \hat {k}$
and
$\Gamma (\hat {k})\gt \hat {k}$
and
 $v\lt \underline {v}$
. Then,
$v\lt \underline {v}$
. Then,
 $k^1_{ss}$
is zero and stable,
$k^1_{ss}$
is zero and stable,
 $k^2_{ss}$
is unstable, and
$k^2_{ss}$
is unstable, and
 $k^3_{ss}$
is stable if
$k^3_{ss}$
is stable if
 $k^3_{ss}\lt \underline {k}$
and unstable if
$k^3_{ss}\lt \underline {k}$
and unstable if
 $k^3_{ss}\ge \underline {k}$
.
$k^3_{ss}\ge \underline {k}$
.
Proof. See Appendix A.
In the following section, we focus on the stable steady state.
3.3. Comparative statics
We evaluate the capital stock dynamics shown in (16) at the steady state by setting
![]() $k_{t+1}=k_{t}=k_{ss}$
. We then define the implicit function
$k_{t+1}=k_{t}=k_{ss}$
. We then define the implicit function
![]() $I$
as
$I$
as
The implicit function theorem shows that
From (23),
![]() $d k_{ss}/d \bar {h}$
is positive if
$d k_{ss}/d \bar {h}$
is positive if
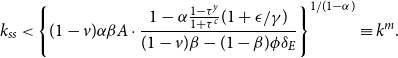 \begin{eqnarray} k_{ss}\lt \left \{ (1-v)\alpha \beta A\cdot \frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma)}{(1-v)\beta -(1-\beta)\phi \delta _E} \right \}^{1/(1-\alpha)}\equiv k^m. \end{eqnarray}
\begin{eqnarray} k_{ss}\lt \left \{ (1-v)\alpha \beta A\cdot \frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma)}{(1-v)\beta -(1-\beta)\phi \delta _E} \right \}^{1/(1-\alpha)}\equiv k^m. \end{eqnarray}
The numerator of
![]() $k^m$
is positive according to Assumption1(b). However, the denominator sign remains ambiguous. If
$k^m$
is positive according to Assumption1(b). However, the denominator sign remains ambiguous. If
![]() $v\ge \bar {v}$
, then the set of capital stocks satisfying (24) is empty. That is,
$v\ge \bar {v}$
, then the set of capital stocks satisfying (24) is empty. That is,
![]() $dk_{ss}/d\bar {h}\lt 0$
if
$dk_{ss}/d\bar {h}\lt 0$
if
![]() $v\ge \bar {v}$
. There is a range
$v\ge \bar {v}$
. There is a range
![]() $[0,k^m)$
that is not empty if
$[0,k^m)$
that is not empty if
![]() $v\lt \bar {v}$
. Then, we have
$v\lt \bar {v}$
. Then, we have
![]() $dk_{ss}/d\bar {h}\gt 0$
for
$dk_{ss}/d\bar {h}\gt 0$
for
![]() $k_{ss}\in [0,k^m)$
, whereas
$k_{ss}\in [0,k^m)$
, whereas
![]() $dk_{ss}/d\bar {h}\le 0$
for
$dk_{ss}/d\bar {h}\le 0$
for
![]() $k_{ss}\ge k^m$
. The discussion thus far is summarized in Proposition2.
$k_{ss}\ge k^m$
. The discussion thus far is summarized in Proposition2.
PROPOSITION 2.
Suppose Assumptions1, 2, and 3 are satisfied. Then, the capital stock in the steady-state equilibrium increases with public investment in adaptation if the steady-state capital stock is ex-ante sufficiently small, such that
![]() $k_{ss}\lt k^m$
and the mitigation subsidy is sufficiently low, such that
$k_{ss}\lt k^m$
and the mitigation subsidy is sufficiently low, such that
![]() $v\lt \bar {v}$
. Conversely, capital stock decreases if
$v\lt \bar {v}$
. Conversely, capital stock decreases if
![]() $v\ge \bar {v}$
or
$v\ge \bar {v}$
or
![]() $k_{ss}\ge k^m$
and
$k_{ss}\ge k^m$
and
![]() $v\lt \bar {v}$
.
$v\lt \bar {v}$
.
![]() $k_{ss}$
increases because the rise in public adaptation investment conditionally crowds out the private provision of mitigation services
$k_{ss}$
increases because the rise in public adaptation investment conditionally crowds out the private provision of mitigation services
![]() $m$
. Then, it allows for more savings when young, more consumption when old, and thereby more pollution, but with a lower effect on agent’s welfare since adaptation has also increased. Thus, when
$m$
. Then, it allows for more savings when young, more consumption when old, and thereby more pollution, but with a lower effect on agent’s welfare since adaptation has also increased. Thus, when
![]() $v$
and
$v$
and
![]() $k_{ss}$
are weak, more adaptation is beneficial.
$k_{ss}$
are weak, more adaptation is beneficial.
We also compute the effects of variations in the environmental regeneration rate. The effect is not so obvious a priori because if pollution absorption increases, the environment improves, and agents will lower their abatement and increase their consumption by saving more when young. However, these effects remain ambiguous.
From (22) and (23), we have
![]() $\mbox{sign}(dk_{ss}/d\delta _E)=\mbox{sign}( -dk_{ss}/d\bar {h})$
. Alternatively, we have
$\mbox{sign}(dk_{ss}/d\delta _E)=\mbox{sign}( -dk_{ss}/d\bar {h})$
. Alternatively, we have
![]() $dl k_{ss}/d \delta _E \gt$
0 if
$dl k_{ss}/d \delta _E \gt$
0 if
![]() $k_{ss}\gt k^m$
. Similarly, the effects of the mitigation rate (abatement rate to pollution rate,
$k_{ss}\gt k^m$
. Similarly, the effects of the mitigation rate (abatement rate to pollution rate,
![]() $\epsilon /\gamma$
) can be derived as
$\epsilon /\gamma$
) can be derived as
We have
![]() $d k_{ss}/d(\epsilon /\gamma)\gt 0$
if
$d k_{ss}/d(\epsilon /\gamma)\gt 0$
if
![]() $k_{ss}\lt k^m$
. If the ratio increases, then the conclusions are the same as those for
$k_{ss}\lt k^m$
. If the ratio increases, then the conclusions are the same as those for
![]() $\bar {h}$
. That is,
$\bar {h}$
. That is,
![]() $(\epsilon /\gamma)$
increases steady-state capital stock if
$(\epsilon /\gamma)$
increases steady-state capital stock if
![]() $k_{ss}$
is sufficiently low.
$k_{ss}$
is sufficiently low.
The effects of other policies on the steady-state capital stock level can also be derived.
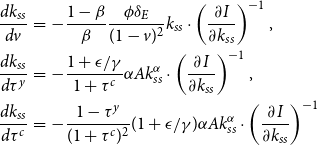 \begin{eqnarray*} \frac {d k_{ss}}{dv} &=& -\frac {1-\beta }{\beta }\frac {\phi \delta _E}{(1-v)^2} k_{ss} \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1},\\ \frac {d k_{ss}}{d\tau ^y} &=& -\frac {1+\epsilon /\gamma }{1+\tau ^c}\alpha Ak_{ss}^\alpha \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1},\\ \frac {d k_{ss}}{d\tau ^c} &=& - \frac {1-\tau ^y}{(1+\tau ^c)^2}(1+\epsilon /\gamma)\alpha Ak_{ss}^\alpha \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1} \end{eqnarray*}
\begin{eqnarray*} \frac {d k_{ss}}{dv} &=& -\frac {1-\beta }{\beta }\frac {\phi \delta _E}{(1-v)^2} k_{ss} \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1},\\ \frac {d k_{ss}}{d\tau ^y} &=& -\frac {1+\epsilon /\gamma }{1+\tau ^c}\alpha Ak_{ss}^\alpha \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1},\\ \frac {d k_{ss}}{d\tau ^c} &=& - \frac {1-\tau ^y}{(1+\tau ^c)^2}(1+\epsilon /\gamma)\alpha Ak_{ss}^\alpha \cdot \left (\frac {\partial I}{\partial k_{ss}}\right)^{-1} \end{eqnarray*}
These three derivatives are negative if
![]() $k_{ss}\lt k^m$
. The results are summarized below.
$k_{ss}\lt k^m$
. The results are summarized below.
COROLLARY 1.
Suppose Assumptions1, 2, and 3 are satisfied. Then, the capital stock at steady-state equilibrium becomes higher when
![]() $\delta _E$
and
$\delta _E$
and
![]() $\epsilon /\gamma$
are higher if
$\epsilon /\gamma$
are higher if
![]() $k_{ss}\lt k^m$
and
$k_{ss}\lt k^m$
and
![]() $v\lt \bar {v}$
. Furthermore, the mitigation subsidy, output tax, and consumption tax decrease steady-state capital stock if
$v\lt \bar {v}$
. Furthermore, the mitigation subsidy, output tax, and consumption tax decrease steady-state capital stock if
![]() $k_{ss}\lt k^m$
and
$k_{ss}\lt k^m$
and
![]() $v\lt \bar {v}$
.
$v\lt \bar {v}$
.
This result is interesting when we consider the heterogeneity between countries in terms of development and exposure to pollution. Indeed, the net effect of mitigation is all the more beneficial and significant the more developed the country (i.e., high per capita capital stock). Symmetrically, the lower the capital stock, the greater the risk that a low net mitigation efficiency rate will lead the country into decline. Indeed, the capital stock decreases in this ratio if the level of development is not sufficiently high.
From these results, we can assess the effect on consumption and mitigation at the steady state. Indeed, we have
![]() $c_{ss}=\frac {1-\tau ^y}{1+\tau ^c}\alpha Ak_{ss}^\alpha$
from (15). This implies that
$c_{ss}=\frac {1-\tau ^y}{1+\tau ^c}\alpha Ak_{ss}^\alpha$
from (15). This implies that
![]() $c_{ss}$
evolves with
$c_{ss}$
evolves with
![]() $k_{ss}$
. This also depends on the tax variables.
$k_{ss}$
. This also depends on the tax variables.
The same results apply for
![]() $m_{ss}$
from (14), given as
$m_{ss}$
from (14), given as
We show that the effects of public adaptation
![]() $\bar {h}$
on private mitigation
$\bar {h}$
on private mitigation
![]() $m_{ss}$
are ambiguous.
$m_{ss}$
are ambiguous.
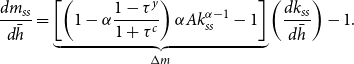 \begin{eqnarray} \frac {d m_{ss}}{d \bar {h}}=\underbrace {\left [ \left ( 1-\alpha \frac {1-\tau ^y}{1+\tau ^c} \right)\alpha Ak_{ss}^{\alpha -1}-1 \right]}_{\Delta m}\left (\frac {d k_{ss}}{d \bar {h}}\right)-1. \end{eqnarray}
\begin{eqnarray} \frac {d m_{ss}}{d \bar {h}}=\underbrace {\left [ \left ( 1-\alpha \frac {1-\tau ^y}{1+\tau ^c} \right)\alpha Ak_{ss}^{\alpha -1}-1 \right]}_{\Delta m}\left (\frac {d k_{ss}}{d \bar {h}}\right)-1. \end{eqnarray}
The last term of (26), that is, −1, represents the resource-constraint effect of public adaptation. If the adaptation is increased, the income available to spend on mitigation reduces by the same proportion. By contrast, when adaptation increases the steady-state capital stock (i.e., the two terms in square brackets,
![]() $\Delta m$
), it increases the current output, which leads to higher mitigation, whereas the increased savings lead to lower mitigation. Consequently, if the first term,
$\Delta m$
), it increases the current output, which leads to higher mitigation, whereas the increased savings lead to lower mitigation. Consequently, if the first term,
![]() $\Delta m\cdot \frac {dk_{ss}}{d\bar {h}}$
, is greater than unity, mitigation increases with adaptation.
$\Delta m\cdot \frac {dk_{ss}}{d\bar {h}}$
, is greater than unity, mitigation increases with adaptation.
However, because the sign of
![]() $\Delta m$
is ambiguous, we must examine it more closely. The term
$\Delta m$
is ambiguous, we must examine it more closely. The term
![]() $\Delta m$
becomes positive if the increase in output is greater than the increase in savings.
$\Delta m$
becomes positive if the increase in output is greater than the increase in savings.
![]() $\Delta m$
is positive if the capital stock in the steady state is sufficiently small such that
$\Delta m$
is positive if the capital stock in the steady state is sufficiently small such that
![]() $k^n$
is positive for all
$k^n$
is positive for all
![]() $v$
and is greater than
$v$
and is greater than
![]() $k^m$
if
$k^m$
if
![]() $v\lt 1-\frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}}{\alpha \frac {1-\tau ^y}{1+\tau ^c} \frac {\epsilon }{\gamma }} \frac {1-\beta }{\beta }\phi \delta _E\equiv \hat {v}$
. We have
$v\lt 1-\frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}}{\alpha \frac {1-\tau ^y}{1+\tau ^c} \frac {\epsilon }{\gamma }} \frac {1-\beta }{\beta }\phi \delta _E\equiv \hat {v}$
. We have
![]() $\hat {v}\lt \bar {v}$
from Assumption1 (b).
$\hat {v}\lt \bar {v}$
from Assumption1 (b).
As a result, mitigation and adaptation increase at the same time under certain conditions on the mitigation subsidy and capital stock level. Then, adaptation and mitigation are complements. The effect of
![]() $\bar {h}$
on
$\bar {h}$
on
![]() $k_{ss}$
is very important in the transmission channels. The greater the effect, the stronger the complementarity. Otherwise, they are considered substitutes. Proposition3 summarizes this discussion.
$k_{ss}$
is very important in the transmission channels. The greater the effect, the stronger the complementarity. Otherwise, they are considered substitutes. Proposition3 summarizes this discussion.
PROPOSITION 3.
Suppose Assumptions1, 2, and 3 are satisfied. Then, mitigation and adaptation are complements if the steady-state capital stock is sufficiently small such that
![]() $k_{ss}\lt k^m$
and
$k_{ss}\lt k^m$
and
![]() $k_{ss}\lt k^n$
, or large such that
$k_{ss}\lt k^n$
, or large such that
![]() $k_{ss}\gt k^m$
and
$k_{ss}\gt k^m$
and
![]() $k_{ss}\gt k_n$
, so that
$k_{ss}\gt k_n$
, so that
![]() $\Delta m \frac {dk_{ss}}{d\bar {h}}\gt 1$
.
$\Delta m \frac {dk_{ss}}{d\bar {h}}\gt 1$
.
Proof. See Appendix B
Whether mitigation and adaptation are complementary or substitutionary depends, as already shown in the literature,Footnote
4
on the level of economic development (
![]() $k$
), but also on the accompanying environmental policy, namely, pollution taxation and mitigation subsidies. This last result is in line with the results of the work of Habla and Roeder (Reference Habla and Roeder2017).
$k$
), but also on the accompanying environmental policy, namely, pollution taxation and mitigation subsidies. This last result is in line with the results of the work of Habla and Roeder (Reference Habla and Roeder2017).
4. Welfare analysis
We determine the optimal levels of investment for (i) mitigationof and (ii) adaptation to climate change. The objective is to definethe optimal policies to be implemented.
4.1. The social optimum
First, we derive the optimal solution, which is the benchmark. Following Ono (Reference Ono1996), we suppose that the benevolent social planner treats all generations symmetrically. There is no intergenerational discounting and we assume that there exists a unique and stable long-term optimal allocation. The latter should guide public policy over the very long term, and thus help to determine the optimal instruments. Then, the problem is to maximize
![]() $u=c^\beta \cdot (E^{-\phi }\cdot H^{\mu })^{1-\beta }$
subject to
$u=c^\beta \cdot (E^{-\phi }\cdot H^{\mu })^{1-\beta }$
subject to
![]() $H=(\bar {H}+h)/\delta _H$
,
$H=(\bar {H}+h)/\delta _H$
,
![]() $E=(\epsilon c -\gamma m)/\delta _E$
, and
$E=(\epsilon c -\gamma m)/\delta _E$
, and
![]() $Ak^\alpha =c+k+m+h$
.
$Ak^\alpha =c+k+m+h$
.
By defining
![]() $A_0\equiv (\alpha A)^{1/1-\alpha }\frac {1-\alpha }{\alpha }$
, we can derive the optimal allocation as follows:
$A_0\equiv (\alpha A)^{1/1-\alpha }\frac {1-\alpha }{\alpha }$
, we can derive the optimal allocation as follows:
To rule out trivial results, we assume the following parameter conditions:
Assumption 4.
![]() $\frac {\mu (1-\beta)A_0}{\beta -(1-\beta)\phi }\gt \bar {H}.$
$\frac {\mu (1-\beta)A_0}{\beta -(1-\beta)\phi }\gt \bar {H}.$
This assumption implies a not too high natural stock of adaptation
![]() $\bar {H}$
. Under Assumption4, the optimal investment in adaptation
$\bar {H}$
. Under Assumption4, the optimal investment in adaptation
![]() $h^*$
in (31) decreases with the natural adaptation stock
$h^*$
in (31) decreases with the natural adaptation stock
![]() $\bar {H}$
. This is because natural adaptation increases the adaptation stock
$\bar {H}$
. This is because natural adaptation increases the adaptation stock
![]() $H^*$
in (32) and decreases the marginal utility from the investment in adaptation. Conversely, natural adaptation,
$H^*$
in (32) and decreases the marginal utility from the investment in adaptation. Conversely, natural adaptation,
![]() $\bar {H}$
, increases investment in mitigation,
$\bar {H}$
, increases investment in mitigation,
![]() $m^*$
in (30), and consumption,
$m^*$
in (30), and consumption,
![]() $c^*$
in (33). The mechanism is as follows: Natural adaptation,
$c^*$
in (33). The mechanism is as follows: Natural adaptation,
![]() $\bar {H}$
, decreases
$\bar {H}$
, decreases
![]() $h^*$
, whereas it has no effect on the capital stock level,
$h^*$
, whereas it has no effect on the capital stock level,
![]() $k^*$
in (28). The saved investment in
$k^*$
in (28). The saved investment in
![]() $h^*$
thus increases
$h^*$
thus increases
![]() $c^*$
and
$c^*$
and
![]() $m^*$
via the resource constraint. We also note that any increase in natural adaptation increase the optimal level of the pollution stock,
$m^*$
via the resource constraint. We also note that any increase in natural adaptation increase the optimal level of the pollution stock,
![]() $E^*$
in (29), as increased natural adaptation decreases the effect on utility from pollution emissions. In addition, following the increase in natural adaptation, the increase in emissions due to increased consumption is greater than the decrease in emissions due to the increase in mitigation; the stock of pollutants increases, that is,
$E^*$
in (29), as increased natural adaptation decreases the effect on utility from pollution emissions. In addition, following the increase in natural adaptation, the increase in emissions due to increased consumption is greater than the decrease in emissions due to the increase in mitigation; the stock of pollutants increases, that is,
![]() $\epsilon \cdot (\partial c^*/\partial \bar {H})\gt \gamma \cdot (\partial m^*/\partial \bar {H})$
hence,
$\epsilon \cdot (\partial c^*/\partial \bar {H})\gt \gamma \cdot (\partial m^*/\partial \bar {H})$
hence,
![]() $(\partial E^*/\partial \bar {H})\gt 0$
.
$(\partial E^*/\partial \bar {H})\gt 0$
.
The optimal mix between mitigation and adaptation can besummarized by the ratio
![]() $(m^*/h^*)$
:
$(m^*/h^*)$
:
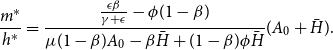 \begin{eqnarray} \frac {m^*}{h^*}=\frac {\frac {\epsilon \beta }{\gamma +\epsilon }-\phi (1-\beta)}{\mu (1-\beta)A_0-\beta \bar {H}+(1-\beta)\phi \bar {H}}(A_0+\bar {H}). \end{eqnarray}
\begin{eqnarray} \frac {m^*}{h^*}=\frac {\frac {\epsilon \beta }{\gamma +\epsilon }-\phi (1-\beta)}{\mu (1-\beta)A_0-\beta \bar {H}+(1-\beta)\phi \bar {H}}(A_0+\bar {H}). \end{eqnarray}
We can easily observe that this ratio decreases with
![]() $\mu$
,
$\mu$
,
![]() $\phi$
, and
$\phi$
, and
![]() $\gamma /\epsilon$
. That is, when the effects on utility from adaptation and pollution become greater (
$\gamma /\epsilon$
. That is, when the effects on utility from adaptation and pollution become greater (
![]() $\mu$
and
$\mu$
and
![]() $\phi$
), adaptation should be increased, rather than mitigation. Furthermore, even when mitigation efficiency is higher, adaptation is increased more than mitigation in the optimal policy plan.
$\phi$
), adaptation should be increased, rather than mitigation. Furthermore, even when mitigation efficiency is higher, adaptation is increased more than mitigation in the optimal policy plan.
4.2. Optimal policy schemes
The economy is characterized by four inefficiencies: dynamic inefficiency, pollution externality, public provision of adaptation, and private contribution to mitigation (Ono, Reference Ono1996). We need to determine the optimal values of the policy instruments, that is,
![]() $\tau ^c$
,
$\tau ^c$
,
![]() $\bar {h}$
,
$\bar {h}$
,
![]() $\tau ^y$
, and
$\tau ^y$
, and
![]() $v$
: (i)
$v$
: (i)
![]() $c_{ss}/E_{ss}=c^*/E^*$
, (ii)
$c_{ss}/E_{ss}=c^*/E^*$
, (ii)
![]() $\bar {h}=h^*$
, (iii)
$\bar {h}=h^*$
, (iii)
![]() $m_{ss}=m^*$
, and (iv)
$m_{ss}=m^*$
, and (iv)
![]() $k_{ss}=k^*$
.
$k_{ss}=k^*$
.
First, we derive
![]() $\tau ^c(\tau ^y,v)$
from (i), which satisfies:
$\tau ^c(\tau ^y,v)$
from (i), which satisfies:
Second, we set the adaptation
![]() $\bar {h}$
directly from (ii) as
$\bar {h}$
directly from (ii) as
![]() $\bar {h}=h^*$
in (31). Third, mitigation satisfies (iii) by setting
$\bar {h}=h^*$
in (31). Third, mitigation satisfies (iii) by setting
![]() $v(\tau ^y,\tau ^c)$
which equalizes the following:
$v(\tau ^y,\tau ^c)$
which equalizes the following:
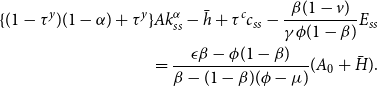 \begin{eqnarray} \{(1-\tau ^y)(1-\alpha)+\tau ^y\}Ak_{ss}^\alpha -\bar {h}+\tau ^c c_{ss}-\frac {\beta (1-v)}{\gamma \phi (1-\beta)}E_{ss}\nonumber \\ =\frac {\epsilon \beta -\phi (1-\beta)}{\beta -(1-\beta)(\phi -\mu)}(A_0+\bar {H}). \end{eqnarray}
\begin{eqnarray} \{(1-\tau ^y)(1-\alpha)+\tau ^y\}Ak_{ss}^\alpha -\bar {h}+\tau ^c c_{ss}-\frac {\beta (1-v)}{\gamma \phi (1-\beta)}E_{ss}\nonumber \\ =\frac {\epsilon \beta -\phi (1-\beta)}{\beta -(1-\beta)(\phi -\mu)}(A_0+\bar {H}). \end{eqnarray}
Finally,
![]() $\tau _y$
is set to derive (iv). Given that
$\tau _y$
is set to derive (iv). Given that
![]() $(1+\tau ^c)c_{ss}=R_{ss}s_{ss}$
from (6),
$(1+\tau ^c)c_{ss}=R_{ss}s_{ss}$
from (6),
![]() $R_ss=(1-\tau ^y)\alpha k_{ss}^{\alpha -1}$
from (9), and the law of motion in the capital market is
$R_ss=(1-\tau ^y)\alpha k_{ss}^{\alpha -1}$
from (9), and the law of motion in the capital market is
![]() $k_{ss}=s_{ss}$
, we can describe
$k_{ss}=s_{ss}$
, we can describe
![]() $\tau ^y$
such that
$\tau ^y$
such that
From the discussion in this subsection, we obtain the following proposition.
PROPOSITION 4. An environmental policy combining optimal taxes on output and consumption, a mitigation subsidy, and constant public investment in adaptation can achieve optimal allocation.
4.3. Numerical simulation
To illustrate how the model performs, this section reports the results from some simple numerical examples. We show that the economy can converge towards a unique and stable long-run steady-state, and that a stable social optimum exists. The objective is also to show that assumptions1 to 4 for the existence and stability of steady-states can be satisfied simultaneously, for reasonable parameter values. We limit our simulations on cases where a non-zero steady-state exists (case (iii) with a sufficiently high mitigation subsidy and case (ix) with a low one).
We set the values of the parameters
![]() $\left \{ \beta,\alpha,\phi,\gamma,\epsilon,\delta _{E}\right \}$
using the estimates usually found in the literature on applied models, and in order to comply with the conditions imposed by assumptions
$\left \{ \beta,\alpha,\phi,\gamma,\epsilon,\delta _{E}\right \}$
using the estimates usually found in the literature on applied models, and in order to comply with the conditions imposed by assumptions
![]() $1$
to
$1$
to
![]() $4$
. To select the environmental parameters we used Bonen et al. (Reference Bonen, Loungani, Semmler and Koch2016) for guidance. We also followed Catalano et al. (Reference Catalano, Forni and Pezzolla2020a, b) and Fried et al. (Reference Fried, Novan and Peterman2018) in order to maintain comparability with other life-cycle studies. The rest of the parameters are reasonably standard within the life-cycle literature. We choose the values for the exogenous parameters as shown in Table 1.
$4$
. To select the environmental parameters we used Bonen et al. (Reference Bonen, Loungani, Semmler and Koch2016) for guidance. We also followed Catalano et al. (Reference Catalano, Forni and Pezzolla2020a, b) and Fried et al. (Reference Fried, Novan and Peterman2018) in order to maintain comparability with other life-cycle studies. The rest of the parameters are reasonably standard within the life-cycle literature. We choose the values for the exogenous parameters as shown in Table 1.
Table 1. Parameter values

Concerning assumption about the consequences of adaptation, it is difficult to make comparisons with assumptions and results from other models.
Indeed, we assume that adaptation helps limit the effects of pollution on welfare, which is a subjective consequence. Empirical studies assessing the consequences of adaptation generally focus on objective physical indicators such as mortality risk (Carleton et al. Reference Carleton, Jina, Delgado, Greenstone, Houser, Hsiang, Hultgren, Kopp, McCusker, Nath, Rising, Rode, Seo, Viaene, Yuan and Zhang2022), agricultural yield (Hultgren et al. Reference Hultgren, Carleton, Delgado, Gergel, Greenstone, Houser, Hsiang, Jina, Kopp, Malevich, McCusker, Mayer, Nath, Rising, Rode and Yuan2022), factor productivity (Catalano et al. Reference Catalano, Forni and Pezzolla2020a, Reference Catalano, Forni and Pezzollab) or factor mobility (like migration). On the other hand, Bonen et al. (Reference Bonen, Loungani, Semmler and Koch2016) considers transmission channels for adaptation expenditure relatively close to our assumptions. Bonen et al. (Reference Bonen, Loungani, Semmler and Koch2016) introduces adaptation expenditure into the utility function, but as a flow of public expenditure and not as a stock of infrastructure or knowledge for adaptation. They assume a value for the elasticity of public capital used for adaptation in utility equal to 0.05, whereas we consider a value of 0.09, but for the impact of the adaptation stock.
First, we calculate the social optimal values, which depend only on technological (
![]() $A,\alpha$
) and environmental (
$A,\alpha$
) and environmental (
![]() $\gamma,\epsilon,\bar {H},\delta _{H},\delta _{E}$
) parameters and preferences (
$\gamma,\epsilon,\bar {H},\delta _{H},\delta _{E}$
) parameters and preferences (
![]() $\beta,\phi,\mu$
). As a benchmark, we obtain the optimal level of adaptation expenditure (
$\beta,\phi,\mu$
). As a benchmark, we obtain the optimal level of adaptation expenditure (
![]() $h$
) equal to 0.04. Then, we evaluate steady-states under different scenarios relating to budget spending. We present two alternative scenarios: in Table 2, the subsidy to mitigation
$h$
) equal to 0.04. Then, we evaluate steady-states under different scenarios relating to budget spending. We present two alternative scenarios: in Table 2, the subsidy to mitigation
![]() $v$
is low (equal to 0), while in Table 3, the subsidy is high (
$v$
is low (equal to 0), while in Table 3, the subsidy is high (
![]() $v=0.9$
). We add to these two policies decisions where the government engages in over- (resp. under-) spending on adaptation (
$v=0.9$
). We add to these two policies decisions where the government engages in over- (resp. under-) spending on adaptation (
![]() $\bar {h}=0.15\gt h^{\ast }$
resp.
$\bar {h}=0.15\gt h^{\ast }$
resp.
![]() $\bar {h}=0.029\lt h^{\ast }$
). These policies are combined with two tax schemes: laissez-faire
$\bar {h}=0.029\lt h^{\ast }$
). These policies are combined with two tax schemes: laissez-faire
![]() $\tau ^{y}=\tau ^{c}=0$
and taxation with
$\tau ^{y}=\tau ^{c}=0$
and taxation with
![]() $\tau ^{y}=0.2$
and
$\tau ^{y}=0.2$
and
![]() $\tau ^{c}=0.1$
.
$\tau ^{c}=0.1$
.
Table 2. Low mitigation subsidy (
![]() $v=0$
)
$v=0$
)
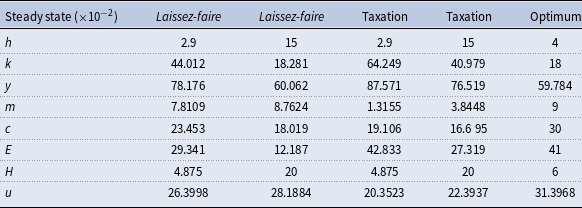
Table 3. High mitigation subsidy (
![]() $v=0.9$
)
$v=0.9$
)
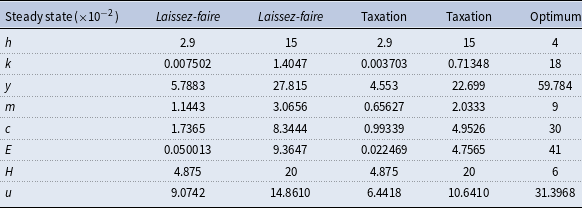
A first important result is that the level of subsidy
![]() $v$
significantly determines capital intensity at steady state. When the subsidy is low (Table 2), the economy is in a situation of capital over-accumulation, whereas a high subsidy (Table 3) causes capital to fall drastically, and the economy is then characterized by under-accumulation. We confirm the results in Proposition2. The increase in expenditure on adaptation (
$v$
significantly determines capital intensity at steady state. When the subsidy is low (Table 2), the economy is in a situation of capital over-accumulation, whereas a high subsidy (Table 3) causes capital to fall drastically, and the economy is then characterized by under-accumulation. We confirm the results in Proposition2. The increase in expenditure on adaptation (
![]() $\bar {h}$
increases from 0.029 to 0.15) reduces the capital stock per capita in a situation of over-accumulation. Conversely, in a situation of under-accumulation, the rise in
$\bar {h}$
increases from 0.029 to 0.15) reduces the capital stock per capita in a situation of over-accumulation. Conversely, in a situation of under-accumulation, the rise in
![]() $\bar {h}$
increases
$\bar {h}$
increases
![]() $k$
. In both cases, adaptation is beneficial in terms of well-being because
$k$
. In both cases, adaptation is beneficial in terms of well-being because
![]() $k$
moves closer to its optimum value. More generally, any increase in the subsidy
$k$
moves closer to its optimum value. More generally, any increase in the subsidy
![]() $v$
worsens the capital stock per capita, whatever the adaptation effort.
$v$
worsens the capital stock per capita, whatever the adaptation effort.
A second significant result relates to the impact on mitigation
![]() $m$
chosen by households. Private spending on mitigation has a twofold impact on pollution. A direct effect is to reduce the stock of pollution through the accumulation of pollutants, and an indirect effect is to reduce savings and hence consumption, the sole source of pollution. When the subsidy to mitigation is low (Table 2), the increase in
$m$
chosen by households. Private spending on mitigation has a twofold impact on pollution. A direct effect is to reduce the stock of pollution through the accumulation of pollutants, and an indirect effect is to reduce savings and hence consumption, the sole source of pollution. When the subsidy to mitigation is low (Table 2), the increase in
![]() $m$
is accompanied by a reduction in economic activity, consumption and therefore pollution. This situation is pareto-improving because the economy is over-accumulating capital. On the other hand, when the subsidy is high (Table 3), the opposite mechanisms are at work, since the increase in
$m$
is accompanied by a reduction in economic activity, consumption and therefore pollution. This situation is pareto-improving because the economy is over-accumulating capital. On the other hand, when the subsidy is high (Table 3), the opposite mechanisms are at work, since the increase in
![]() $m$
goes hand in hand with an increase in
$m$
goes hand in hand with an increase in
![]() $k,c$
and therefore
$k,c$
and therefore
![]() $E$
. In this case too, these changes are beneficial in terms of welfare despite the rise in pollution. Indeed, the increase in
$E$
. In this case too, these changes are beneficial in terms of welfare despite the rise in pollution. Indeed, the increase in
![]() $m,c$
and
$m,c$
and
![]() $k$
follows an increase in
$k$
follows an increase in
![]() $\bar {h}$
: households consume more and are better protected against pollution. In this example, we show that any increase in
$\bar {h}$
: households consume more and are better protected against pollution. In this example, we show that any increase in
![]() $\bar {h}$
leads to an increase in
$\bar {h}$
leads to an increase in
![]() $m$
, whatever the tax scheme (
$m$
, whatever the tax scheme (
![]() $v,\tau ^{y},\tau ^{c}$
). We are therefore in a situation where adaptation and mitigation are complements (see Proposition3).
$v,\tau ^{y},\tau ^{c}$
). We are therefore in a situation where adaptation and mitigation are complements (see Proposition3).
We find the results of corollary1 on the impact of instruments (i.e., laissez-faire vs taxation) on the capital stock per capita. When the latter is high (i.e.,
![]() $v$
low, Table 2), higher taxes increase the capital stock, whereas the effect is negative when the capital stock is low (Table 3).
$v$
low, Table 2), higher taxes increase the capital stock, whereas the effect is negative when the capital stock is low (Table 3).
When the mitigation subsidy is small (Table 2), the level of mitigation is low (relative to the optimum), and counter-intuitively, the level of pollution is also small. This result can be explained by the high level of the capital stock per capita, which absorbs the greater part of the production of goods, and which does not pollute, unlike consumption. This effect is even stronger when expenditure on adaptation is high (
![]() $\bar {h} =0.15$
), reflecting a substitution between consumption and adaptation to the environment. As a result, welfare increases. Note that when the mitigation subsidy is high, private mitigation choices and capital per capita are highly sensitive to public decisions on adaptation (
$\bar {h} =0.15$
), reflecting a substitution between consumption and adaptation to the environment. As a result, welfare increases. Note that when the mitigation subsidy is high, private mitigation choices and capital per capita are highly sensitive to public decisions on adaptation (
![]() $\bar {h}$
).
$\bar {h}$
).
5. Extensions
5.1. Proportional adaptation
We suppose a case in which the adaptation level is determined by the flow of pollutants. This implies that, in a sense, mitigation influences adaptation. Hence, if mitigation increases, it implies a lower consumption level (budget constraint) and adaptation level. We extend the previous results to the case where the investment in adaptation is set proportionally to the flow of pollution at a constant rate
![]() $z\ge 0$
:
$z\ge 0$
:
This policy implies a relationship between the current adaptation
![]() $h_t$
and previous mitigation
$h_t$
and previous mitigation
![]() $m_{t-1}$
. Indeed,
$m_{t-1}$
. Indeed,
![]() $h_t$
must increase if consumption
$h_t$
must increase if consumption
![]() $c_t$
increases. This is possible if savings
$c_t$
increases. This is possible if savings
![]() $s_{t-1}$
increases and mitigation
$s_{t-1}$
increases and mitigation
![]() $m_{t-1}$
decreases, ceteris paribus.
$m_{t-1}$
decreases, ceteris paribus.
By substituting (38) into (11) and using (8), (9), and (12), the dynamics of capital stock per young are given by
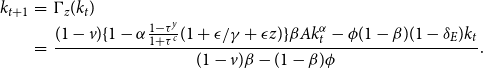 \begin{eqnarray} k_{t+1}&=&\Gamma _z(k_t)\nonumber \\ &=&\frac {(1-v)\{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \}\beta Ak_t^\alpha - \phi (1-\beta)(1-\delta _E)k_t}{(1-v)\beta - (1-\beta)\phi }. \end{eqnarray}
\begin{eqnarray} k_{t+1}&=&\Gamma _z(k_t)\nonumber \\ &=&\frac {(1-v)\{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \}\beta Ak_t^\alpha - \phi (1-\beta)(1-\delta _E)k_t}{(1-v)\beta - (1-\beta)\phi }. \end{eqnarray}
In this case, we have two steady states with
![]() $k^1_{ss}$
and
$k^1_{ss}$
and
![]() $k^2_{ss}$
such that
$k^2_{ss}$
such that
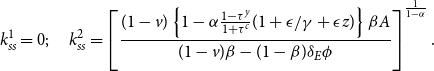 \begin{eqnarray} k^1_{ss}=0; \;\;\;\;\;\; k^2_{ss}=\left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \} \beta A}{(1-v)\beta -(1-\beta)\delta _E\phi }\right]^{\frac {1}{1-\alpha }}. \end{eqnarray}
\begin{eqnarray} k^1_{ss}=0; \;\;\;\;\;\; k^2_{ss}=\left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \} \beta A}{(1-v)\beta -(1-\beta)\delta _E\phi }\right]^{\frac {1}{1-\alpha }}. \end{eqnarray}
Let us consider the conditions for positive capital stock in a non-trivial steady state,
![]() $k_{ss}^2\gt 0$
. This is easily attained by assuming that
$k_{ss}^2\gt 0$
. This is easily attained by assuming that
![]() $\frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}{(1-v)\beta -(1-\beta)\delta _E\phi }\gt 0.$
On the one hand, the denominator becomes negative (resp. positive) if the mitigation subsidy is greater than
$\frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}{(1-v)\beta -(1-\beta)\delta _E\phi }\gt 0.$
On the one hand, the denominator becomes negative (resp. positive) if the mitigation subsidy is greater than
![]() $\bar {v}$
(resp. lower than
$\bar {v}$
(resp. lower than
![]() $\bar {v}$
). On the other hand, the numerator can also be negative (resp. positive) if the adaptation provision rate
$\bar {v}$
). On the other hand, the numerator can also be negative (resp. positive) if the adaptation provision rate
![]() $z$
is greater than
$z$
is greater than
![]() $\bar {z}$
(resp. lower than
$\bar {z}$
(resp. lower than
![]() $\bar {z}$
), as defined below.
$\bar {z}$
), as defined below.
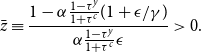 \begin{eqnarray} \bar {z}\equiv \frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma)}{\alpha \frac {1-\tau ^y}{1+\tau ^c}\epsilon }\gt 0. \end{eqnarray}
\begin{eqnarray} \bar {z}\equiv \frac {1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma)}{\alpha \frac {1-\tau ^y}{1+\tau ^c}\epsilon }\gt 0. \end{eqnarray}
From Assumption1(b),
![]() $\bar {z}$
is positive. For the nontrivial steady state with
$\bar {z}$
is positive. For the nontrivial steady state with
![]() $k_{ss}^2$
, we suppose that the environmental policy tools satisfy the following:
$k_{ss}^2$
, we suppose that the environmental policy tools satisfy the following:
Assumption 5.
We assume that either (i)
![]() $z\lt \bar {z}$
and
$z\lt \bar {z}$
and
![]() $v\lt \bar {v}$
or (ii)
$v\lt \bar {v}$
or (ii)
![]() $z\gt \bar {z}$
and
$z\gt \bar {z}$
and
![]() $v\gt \bar {v}$
.
$v\gt \bar {v}$
.
This assumption requires either sufficiently large or sufficiently small mitigation and adaptation. We therefore exclude intermediate cross-cases in order to restrict the analysis to situations where there exist two stationary states with at least one non-trivial stable steady state.
To examine the stability of the steady state, we define
![]() $\overline {k_z}$
,
$\overline {k_z}$
,
![]() $\underline {k_z}$
, and
$\underline {k_z}$
, and
![]() $\hat {k_z}$
as follows.
$\hat {k_z}$
as follows.
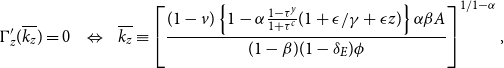 \begin{eqnarray} \Gamma _z^{\prime}(\overline {k_z})=0 \;\;\; &\Leftrightarrow & \;\;\; \overline {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-\beta)(1-\delta _E)\phi } \right]^{1/1-\alpha }, \end{eqnarray}
\begin{eqnarray} \Gamma _z^{\prime}(\overline {k_z})=0 \;\;\; &\Leftrightarrow & \;\;\; \overline {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-\beta)(1-\delta _E)\phi } \right]^{1/1-\alpha }, \end{eqnarray}
 \begin{eqnarray} \Gamma _z^{\prime}(\underline {k_z})=-1 \;\;\; &\Leftrightarrow & \;\;\; \underline {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-\beta)(2-\delta _E)\phi -(1-v)\beta } \right]^{1/1-\alpha }, \end{eqnarray}
\begin{eqnarray} \Gamma _z^{\prime}(\underline {k_z})=-1 \;\;\; &\Leftrightarrow & \;\;\; \underline {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-\beta)(2-\delta _E)\phi -(1-v)\beta } \right]^{1/1-\alpha }, \end{eqnarray}
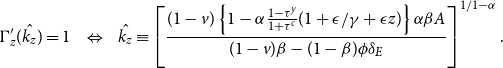 \begin{eqnarray} \Gamma _z^{\prime}(\hat {k_z})=1 \;\;\; &\Leftrightarrow & \;\;\; \hat {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-v)\beta -(1-\beta)\phi \delta _E} \right]^{1/1-\alpha }. \end{eqnarray}
\begin{eqnarray} \Gamma _z^{\prime}(\hat {k_z})=1 \;\;\; &\Leftrightarrow & \;\;\; \hat {k_z}\equiv \left [ \frac {(1-v)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z) \right \}\alpha \beta A}{(1-v)\beta -(1-\beta)\phi \delta _E} \right]^{1/1-\alpha }. \end{eqnarray}
Consequently, from (39), Proposition5 characterizes the steady-state equilibrium with proportional adaptation.
PROPOSITION 5.
Suppose a proportional adaptation to the flow ofpollutants, and Assumptions1, 2, 3, and 5 are satisfied. Then, thereare two steady-state equilibria with capital stocks
![]() $k_{ss}^1=0$
and
$k_{ss}^1=0$
and
![]() $k_{ss}^2\gt 0$
. The stability properties of these steady states are presented in the following four cases.
$k_{ss}^2\gt 0$
. The stability properties of these steady states are presented in the following four cases.
-
(i) Suppose
 $v\gt \bar {v}$
and
$v\gt \bar {v}$
and
 $z\gt \bar {z}$
. Then, the steady state with
$z\gt \bar {z}$
. Then, the steady state with
 $k_{ss}^1$
is unstable, whereas that with
$k_{ss}^1$
is unstable, whereas that with
 $k_{ss}^2$
is stable.
$k_{ss}^2$
is stable.
-
(ii) Suppose
 $v\lt \bar {v}$
and
$v\lt \bar {v}$
and
 $z\lt \bar {z}$
. Especially, if
$z\lt \bar {z}$
. Especially, if
 $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
 $k_{ss}^2\lt \underline {k_z}$
, the steady state with
$k_{ss}^2\lt \underline {k_z}$
, the steady state with
 $k_{ss}^1$
is unstable, whereas that with
$k_{ss}^1$
is unstable, whereas that with
 $k_{ss}^2$
is stable.
$k_{ss}^2$
is stable.
-
(iii) Suppose
 $v\lt \bar {v}$
and
$v\lt \bar {v}$
and
 $z\lt \bar {z}$
. Especially, if
$z\lt \bar {z}$
. Especially, if
 $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
 $k_{ss}^2\ge \underline {k_z}$
, both the steady states are unstable.
$k_{ss}^2\ge \underline {k_z}$
, both the steady states are unstable.
-
(iv) Suppose
 $v\lt \bar {v}$
and
$v\lt \bar {v}$
and
 $z\lt \bar {z}$
. Especially, if
$z\lt \bar {z}$
. Especially, if
 $\underline {v}\le v \lt \bar {v}$
, the steady state with
$\underline {v}\le v \lt \bar {v}$
, the steady state with
 $k_{ss}^1$
is stable, and that with
$k_{ss}^1$
is stable, and that with
 $k_{ss}^2$
is unstable.
$k_{ss}^2$
is unstable.
Proof. See Appendix C.
As well as Proposition1, the mitigation subsidy is a key to the analysis of the dynamics of the capital stock. Depending on whether the subsidy is low or high enough, three cases for each exist. However, as the adaptation level is not fixed in this case, the analysis of the capital stock dynamics is simplified.
From this proposition, we focus on the steady state with
![]() $k_{ss}^2$
in cases (i) and (ii) of Proposition5. The nontrivial steady-state equilibrium is described as follows:
$k_{ss}^2$
in cases (i) and (ii) of Proposition5. The nontrivial steady-state equilibrium is described as follows:
Next, we derive the derivatives of
![]() $k_{ss}^2$
with respect to the policy variables as a comparative statics study.
$k_{ss}^2$
with respect to the policy variables as a comparative statics study.
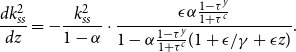 \begin{align} \frac {dk^2_{ss}}{dz}&=-\frac {k_{ss}^2}{1-\alpha }\cdot \frac {\epsilon \alpha \frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
\begin{align} \frac {dk^2_{ss}}{dz}&=-\frac {k_{ss}^2}{1-\alpha }\cdot \frac {\epsilon \alpha \frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
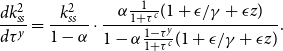 \begin{align} \frac {dk^2_{ss}}{d\tau ^y}&=\frac {k_{ss}^2}{1-\alpha }\cdot \frac { \alpha \frac {1}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
\begin{align} \frac {dk^2_{ss}}{d\tau ^y}&=\frac {k_{ss}^2}{1-\alpha }\cdot \frac { \alpha \frac {1}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
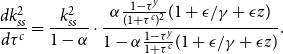 \begin{align} \frac {dk^2_{ss}}{d\tau ^c}&= \frac {k_{ss}^2}{1-\alpha }\cdot \frac { \alpha \frac {1-\tau ^y}{(1+\tau ^c)^2}(1+\epsilon /\gamma +\epsilon z)}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
\begin{align} \frac {dk^2_{ss}}{d\tau ^c}&= \frac {k_{ss}^2}{1-\alpha }\cdot \frac { \alpha \frac {1-\tau ^y}{(1+\tau ^c)^2}(1+\epsilon /\gamma +\epsilon z)}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}. \end{align}
From (50)–(53), we immediately obtain the following corollary.
COROLLARY 2.
Suppose a proportional adaptation to the flow of pollutants, and Assumptions1, 2, 3, and 5 are satisfied. If
![]() $v\gt \bar {v}$
and
$v\gt \bar {v}$
and
![]() $z\gt \bar {z}$
, the adaptation rate (
$z\gt \bar {z}$
, the adaptation rate (
![]() $z$
) increases the steady-state capital stock, whereas the mitigation subsidy rate (
$z$
) increases the steady-state capital stock, whereas the mitigation subsidy rate (
![]() $v$
), output tax (
$v$
), output tax (
![]() $\tau ^y$
), and consumption tax (
$\tau ^y$
), and consumption tax (
![]() $\tau ^c$
) decrease it. By contrast, if
$\tau ^c$
) decrease it. By contrast, if
![]() $v\lt \bar {v}$
and
$v\lt \bar {v}$
and
![]() $z\lt \bar {z}$
, their effects on steady-state capital stock are reversed.
$z\lt \bar {z}$
, their effects on steady-state capital stock are reversed.
This corollary shows that capital stock does not always increase with the adaptation rate
![]() $z$
. This also implies, together with (45) and (47), that the adaptation rate,
$z$
. This also implies, together with (45) and (47), that the adaptation rate,
![]() $z$
, does not always increase the adaptation flow,
$z$
, does not always increase the adaptation flow,
![]() $h_{ss}$
, or the adaptation stock,
$h_{ss}$
, or the adaptation stock,
![]() $H_{ss}$
, in the steady state. To observe this in detail, we have from (46):
$H_{ss}$
, in the steady state. To observe this in detail, we have from (46):
The first term is a direct increase in
![]() $z$
whereas the second is an indirect increase via
$z$
whereas the second is an indirect increase via
![]() $k_{ss}^2$
. We define the fiscal scheme in (38). If
$k_{ss}^2$
. We define the fiscal scheme in (38). If
![]() $z$
decreases the capital stock, the consumption shown in (45) decreases, and thus the indirect effect decreases the adaptation flow and stock. We can rearrange this expression using (46) and (50) as:
$z$
decreases the capital stock, the consumption shown in (45) decreases, and thus the indirect effect decreases the adaptation flow and stock. We can rearrange this expression using (46) and (50) as:
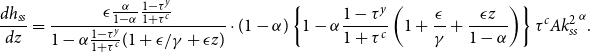 \begin{eqnarray} \frac {dh_{ss}}{dz}=\frac {\epsilon \frac {\alpha }{1-\alpha }\frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}\cdot (1-\alpha)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left (1+\frac {\epsilon }{\gamma }+\frac {\epsilon z}{1-\alpha }\right)\right \}\tau ^c A{k_{ss}^2}^\alpha. \end{eqnarray}
\begin{eqnarray} \frac {dh_{ss}}{dz}=\frac {\epsilon \frac {\alpha }{1-\alpha }\frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}\cdot (1-\alpha)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left (1+\frac {\epsilon }{\gamma }+\frac {\epsilon z}{1-\alpha }\right)\right \}\tau ^c A{k_{ss}^2}^\alpha. \end{eqnarray}
We define
![]() $\underline {z}$
, which satisfies
$\underline {z}$
, which satisfies
![]() $\frac {dh_{ss}}{dz}=0$
:
$\frac {dh_{ss}}{dz}=0$
:
Therefore, the derivative in (54) is strictly positive for
![]() $z\lt \underline {z}$
and strictly negative for
$z\lt \underline {z}$
and strictly negative for
![]() $z\gt \underline {z}$
. Likewise, the effect on mitigation from the adaptation rate is ambiguous, as shown in (48):
$z\gt \underline {z}$
. Likewise, the effect on mitigation from the adaptation rate is ambiguous, as shown in (48):
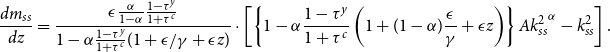 \begin{eqnarray} \frac {dm_{ss}}{dz}=\frac {\epsilon \frac {\alpha }{1-\alpha } \frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}\cdot \left [ \left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left ( 1+(1-\alpha)\frac {\epsilon }{\gamma }+\epsilon z \right) \right \}A{k_{ss}^2}^\alpha -k_{ss}^2 \right]. \quad\,\end{eqnarray}
\begin{eqnarray} \frac {dm_{ss}}{dz}=\frac {\epsilon \frac {\alpha }{1-\alpha } \frac {1-\tau ^y}{1+\tau ^c}}{1-\alpha \frac {1-\tau ^y}{1+\tau ^c}(1+\epsilon /\gamma +\epsilon z)}\cdot \left [ \left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left ( 1+(1-\alpha)\frac {\epsilon }{\gamma }+\epsilon z \right) \right \}A{k_{ss}^2}^\alpha -k_{ss}^2 \right]. \quad\,\end{eqnarray}
From (54) and (56), we obtain the following expression.
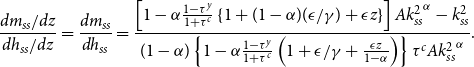 \begin{eqnarray} \frac {dm_{ss}/dz}{dh_{ss}/dz}=\frac {dm_{ss}}{dh_{ss}}=\frac {\left [ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left \{ 1+(1-\alpha)(\epsilon /\gamma)+\epsilon z \right \} \right]A{k_{ss}^2}^\alpha -k_{ss}^2}{ (1-\alpha)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left ( 1+\epsilon /\gamma +\frac {\epsilon z}{1-\alpha } \right) \right \}\tau ^c A {k_{ss}^2}^\alpha }. \end{eqnarray}
\begin{eqnarray} \frac {dm_{ss}/dz}{dh_{ss}/dz}=\frac {dm_{ss}}{dh_{ss}}=\frac {\left [ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left \{ 1+(1-\alpha)(\epsilon /\gamma)+\epsilon z \right \} \right]A{k_{ss}^2}^\alpha -k_{ss}^2}{ (1-\alpha)\left \{ 1-\alpha \frac {1-\tau ^y}{1+\tau ^c}\left ( 1+\epsilon /\gamma +\frac {\epsilon z}{1-\alpha } \right) \right \}\tau ^c A {k_{ss}^2}^\alpha }. \end{eqnarray}
The denominator becomes positive if
![]() $z\lt \underline {z}$
, whereas the square brackets of the numerator become positive if
$z\lt \underline {z}$
, whereas the square brackets of the numerator become positive if
![]() $z\lt \hat {z}$
defined as
$z\lt \hat {z}$
defined as
Then, we have
![]() $\underline {z}\lt \bar {z}\lt \hat {z}$
. In addition to the adaptation rate, the numerator also has a threshold
$\underline {z}\lt \bar {z}\lt \hat {z}$
. In addition to the adaptation rate, the numerator also has a threshold
![]() $k^\ell$
that determines its sign.
$k^\ell$
that determines its sign.
From the discussion thus far, the substitutability between mitigation and adaptation can be summarized as follows:
PROPOSITION 6.
Suppose a proportional adaptation to the flow of pollutants, and Assumptions1, 2, 3, and 5 are satisfied. The mitigation and adaptation are complements if (i)
![]() $z\le \underline {z}$
and
$z\le \underline {z}$
and
![]() $k_{ss}^2\lt k^\ell$
, (ii)
$k_{ss}^2\lt k^\ell$
, (ii)
![]() $\underline {z}\lt z\lt \hat {z}$
and
$\underline {z}\lt z\lt \hat {z}$
and
![]() $k_{ss}^2\gt k^\ell$
, or (iii)
$k_{ss}^2\gt k^\ell$
, or (iii)
![]() $z\ge \hat {z}$
.
$z\ge \hat {z}$
.
Proof. See Appendix D
In the case of constant adaptation investment, mitigation and adaptation can be both complements and substitutes, but this depends on the adaptation rate and capital stock level at the steady state.
5.2. Public debt financing of adaptation
Results thus far assume that public investment in adaptation and mitigation subsidies is financed by taxes on current generations. However, as adaptation is a stock or durable good, it benefits not only the present generations but also future generations. Debt is an instrument that affects intertemporal transfers and intergenerational welfare. We assume that investment in adaptation is partly financed by public debt. This financing policy allows future generations to benefit from the accumulated adaptation stock and partly bear its present cost.
In particular, we suppose that adaptation investment is set at an optimal level at steady state and is totally financed by debt issuing. We focus on equilibria with constant debt per capita, that is,
![]() $B_t=B\gt 0$
for all
$B_t=B\gt 0$
for all
![]() $t\gt 0$
. Debt is constant so that steady-states can be explicitly determined. We consider public debt as an instrument of environmental policy, it finances investments in the adaptation stock. This instrument replaces the production tax. Optimal debt helps to achieve the optimal level of adaptation, as defined by (30) and (31), by substituting
$t\gt 0$
. Debt is constant so that steady-states can be explicitly determined. We consider public debt as an instrument of environmental policy, it finances investments in the adaptation stock. This instrument replaces the production tax. Optimal debt helps to achieve the optimal level of adaptation, as defined by (30) and (31), by substituting
![]() $h^*$
into
$h^*$
into
![]() $\bar {h}$
. Thus, the government budget is given as
$\bar {h}$
. Thus, the government budget is given as
We have the following capital market equilibrium:
Eq. (61) is rewritten as the dynamics of capital stock:
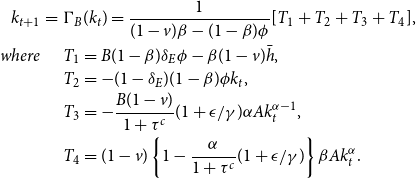 \begin{eqnarray} k_{t+1}&=&\Gamma _B(k_t)=\frac {1}{(1-v)\beta -(1-\beta)\phi }[T_1+T_2+T_3+T_4],\\ where&&T_1=B (1-\beta)\delta _E \phi - \beta (1-v)\bar {h},\nonumber \\ &&T_2= -(1-\delta _E)(1-\beta)\phi k_t,\nonumber \\ &&T_3= -\frac {B(1-v)}{1+\tau ^c}(1+\epsilon /\gamma)\alpha A k_t^{\alpha -1},\nonumber \\ &&T_4= (1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\beta A k_t^\alpha.\nonumber \end{eqnarray}
\begin{eqnarray} k_{t+1}&=&\Gamma _B(k_t)=\frac {1}{(1-v)\beta -(1-\beta)\phi }[T_1+T_2+T_3+T_4],\\ where&&T_1=B (1-\beta)\delta _E \phi - \beta (1-v)\bar {h},\nonumber \\ &&T_2= -(1-\delta _E)(1-\beta)\phi k_t,\nonumber \\ &&T_3= -\frac {B(1-v)}{1+\tau ^c}(1+\epsilon /\gamma)\alpha A k_t^{\alpha -1},\nonumber \\ &&T_4= (1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\beta A k_t^\alpha.\nonumber \end{eqnarray}
With this expression, we obtain the following proposition for the steady-state equilibrium. For stability, we derive the derivatives of (62) as
 \begin{align} \Gamma _B^{\prime}(k_t)&=\frac {1}{(1-v)\beta -(1-\beta)\phi }\left [ -(1-\delta _E)(1-\beta)\phi +B\frac {1-v}{1+\tau ^c}(1-\alpha)(1+\epsilon /\gamma)\alpha Ak_t^{\alpha -2} \right.\nonumber \\ & \quad \left. +(1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A k_t^{\alpha -1} \right]. \end{align}
\begin{align} \Gamma _B^{\prime}(k_t)&=\frac {1}{(1-v)\beta -(1-\beta)\phi }\left [ -(1-\delta _E)(1-\beta)\phi +B\frac {1-v}{1+\tau ^c}(1-\alpha)(1+\epsilon /\gamma)\alpha Ak_t^{\alpha -2} \right.\nonumber \\ & \quad \left. +(1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha \beta A k_t^{\alpha -1} \right]. \end{align}
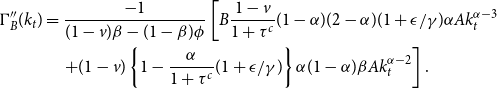 \begin{align} \Gamma _B^{\prime\prime}(k_t)&=\frac {-1}{(1-v)\beta -(1-\beta)\phi }\left [ B\frac {1-v}{1+\tau ^c}(1-\alpha)(2-\alpha)(1+\epsilon /\gamma)\alpha Ak_t^{\alpha -3} \right. \nonumber \\ & \quad \left. +(1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha (1-\alpha)\beta A k_t^{\alpha -2} \right]. \end{align}
\begin{align} \Gamma _B^{\prime\prime}(k_t)&=\frac {-1}{(1-v)\beta -(1-\beta)\phi }\left [ B\frac {1-v}{1+\tau ^c}(1-\alpha)(2-\alpha)(1+\epsilon /\gamma)\alpha Ak_t^{\alpha -3} \right. \nonumber \\ & \quad \left. +(1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1+\epsilon /\gamma) \right \}\alpha (1-\alpha)\beta A k_t^{\alpha -2} \right]. \end{align}
Furthermore, to summarize the stability conditions, we define
![]() $\underline {k_B}$
,
$\underline {k_B}$
,
![]() $\overline {k_B}$
, and
$\overline {k_B}$
, and
![]() $\hat {k_B}$
as
$\hat {k_B}$
as
![]() $\Gamma _B^{\prime}(\underline {k_B})=-1$
,
$\Gamma _B^{\prime}(\underline {k_B})=-1$
,
![]() $\Gamma _B^{\prime}(\overline {k_B})=0$
, and
$\Gamma _B^{\prime}(\overline {k_B})=0$
, and
![]() $\Gamma _B^{\prime}(\hat {k_B})=1$
. These three levels are unique because (64) exhibits monotonicity of
$\Gamma _B^{\prime}(\hat {k_B})=1$
. These three levels are unique because (64) exhibits monotonicity of
![]() $\Gamma _B^{\prime}(k_t)$
.
$\Gamma _B^{\prime}(k_t)$
.
PROPOSITION 7. Suppose investment in adaptation and public debt are constant, and Assumptions1, 2, and 3 are satisfied. Then, the steady-state equilibria and the stability conditions are characterized in the following six cases.
-
(i) Suppose
 $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
 $\Gamma _B(\hat {k_B})\lt \hat {k_B}$
. Then, there is a unique steady state at
$\Gamma _B(\hat {k_B})\lt \hat {k_B}$
. Then, there is a unique steady state at
 $k_{ss}=0$
, and this is stable.
$k_{ss}=0$
, and this is stable.
-
(ii) Suppose
 $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
 $\Gamma _B(\hat {k_B})=\hat {k_B}$
. Then, there are two steady states with
$\Gamma _B(\hat {k_B})=\hat {k_B}$
. Then, there are two steady states with
 $k_{ss}^1=0$
and
$k_{ss}^1=0$
and
 $k_{ss}^2\gt 0$
. The steady state with
$k_{ss}^2\gt 0$
. The steady state with
 $k_{ss}^1=0$
is locally stable and that with
$k_{ss}^1=0$
is locally stable and that with
 $k_{ss}^2$
is unstable.
$k_{ss}^2$
is unstable.
-
(iii) Suppose
 $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
 $\Gamma _B(\hat {k_B})\gt \hat {k_B}$
. Then, there are three steady states with
$\Gamma _B(\hat {k_B})\gt \hat {k_B}$
. Then, there are three steady states with
 $k_{ss}^1=0$
and
$k_{ss}^1=0$
and
 $k_{ss}^2,k_{ss}^3\gt 0$
, where
$k_{ss}^2,k_{ss}^3\gt 0$
, where
 $k_{ss}^2\lt k_{ss}^3$
. The steady state with
$k_{ss}^2\lt k_{ss}^3$
. The steady state with
 $k_{ss}^1=0$
is stable, and that with
$k_{ss}^1=0$
is stable, and that with
 $k_{ss}^2$
is unstable. Furthermore, the steady state with
$k_{ss}^2$
is unstable. Furthermore, the steady state with
 $k_{ss}^3$
is locally stable if
$k_{ss}^3$
is locally stable if
 $k_{ss}^3\lt \underline {k_B}$
, whereas it is unstable if
$k_{ss}^3\lt \underline {k_B}$
, whereas it is unstable if
 $k_{ss}^3\ge \underline {k_B}$
.
$k_{ss}^3\ge \underline {k_B}$
. -
(iv) Suppose
 $v\gt \underline {v}$
and
$v\gt \underline {v}$
and
 $\Gamma _B(\hat {k})\gt \hat {k_B}$
. Then, there is no steady state in a finite range.
$\Gamma _B(\hat {k})\gt \hat {k_B}$
. Then, there is no steady state in a finite range.
-
(v) Suppose
 $v\gt \underline {v}$
and
$v\gt \underline {v}$
and
 $\Gamma _B(\hat {k})=\hat {k_B}$
. Then, there is a unique steady state with
$\Gamma _B(\hat {k})=\hat {k_B}$
. Then, there is a unique steady state with
 $k_{ss}\gt 0$
, and this is unstable.
$k_{ss}\gt 0$
, and this is unstable.
-
(vi) Suppose
 $v\gt \underline {v}$
and
$v\gt \underline {v}$
and
 $\Gamma _B(\hat {k})\lt \hat {k_B}$
. Then, there are two steady states with
$\Gamma _B(\hat {k})\lt \hat {k_B}$
. Then, there are two steady states with
 $k_{ss}^1\gt 0$
and
$k_{ss}^1\gt 0$
and
 $k_{ss}^2\gt 0$
, where
$k_{ss}^2\gt 0$
, where
 $k_{ss}^1\lt k_{ss}^2$
. The steady state with
$k_{ss}^1\lt k_{ss}^2$
. The steady state with
 $k_{ss}^2$
is unstable. By contrast, the steady state with
$k_{ss}^2$
is unstable. By contrast, the steady state with
 $k_{ss}^1$
is locally stable if
$k_{ss}^1$
is locally stable if
 $k_{ss}^1\gt \underline {k_B}$
, and unstable if
$k_{ss}^1\gt \underline {k_B}$
, and unstable if
 $k_{ss}^1\le \underline {k_B}$
.
$k_{ss}^1\le \underline {k_B}$
.
Proof. See Appendix E.
As well as the previous models and as shown in Proposition1 and 5, the capital stock dynamics has two cases, depending on the subsidy rates. For each case, the dynamics have further three cases, depending on the capital stock.
From Proposition7, in the presence of a constant adaptation financed partly by debt, we focus on the locally stable nontrivial steady state, such as
![]() $k_{ss}^3$
in Case (iii) with
$k_{ss}^3$
in Case (iii) with
![]() $k_{ss}^3\lt \underline {k_B}$
and
$k_{ss}^3\lt \underline {k_B}$
and
![]() $k_{ss}^1$
in Case (vi) with
$k_{ss}^1$
in Case (vi) with
![]() $k_{ss}^1\gt \underline {k_B}$
.
$k_{ss}^1\gt \underline {k_B}$
.
We then develop comparative statics with respect to debt. By differentiating
![]() $\Gamma _B(k_t)$
with respect to the constant debt
$\Gamma _B(k_t)$
with respect to the constant debt
![]() $B$
, we haveFootnote
5
$B$
, we haveFootnote
5
This implies that if
![]() $v\lt \underline {v}$
, the dynamics of the capital stock shift upward for
$v\lt \underline {v}$
, the dynamics of the capital stock shift upward for
![]() $k_t\gt k^o$
and downwards for
$k_t\gt k^o$
and downwards for
![]() $k_t\lt k^o$
, where
$k_t\lt k^o$
, where
Because
![]() $B$
can take zero or larger values,
$B$
can take zero or larger values,
![]() $k^o$
can also take a wide range of values. By contrast, if
$k^o$
can also take a wide range of values. By contrast, if
![]() $v\gt \underline {v}$
, the dynamics shift upward if
$v\gt \underline {v}$
, the dynamics shift upward if
![]() $k_t\lt k^o$
and downward if
$k_t\lt k^o$
and downward if
![]() $k_t\gt k^o$
.
$k_t\gt k^o$
.
Given this result, we consider the steady-state effect of debt. For this purpose, we suppose locally stable steady states. First, suppose
![]() $v\lt \underline {v}$
,
$v\lt \underline {v}$
,
![]() $\Gamma _B(\hat {k_B})\gt \hat {k_B}$
, and
$\Gamma _B(\hat {k_B})\gt \hat {k_B}$
, and
![]() $k_{ss}^3\lt \underline {k_B}$
, as in case (iii) of Proposition7. Then, steady-state capital stock
$k_{ss}^3\lt \underline {k_B}$
, as in case (iii) of Proposition7. Then, steady-state capital stock
![]() $k_{ss}^3$
is locally stable. Suppose further that the economy lies on
$k_{ss}^3$
is locally stable. Suppose further that the economy lies on
![]() $k_{ss}=k_{ss}^3$
; if
$k_{ss}=k_{ss}^3$
; if
![]() $k_{ss}^3\gt k^o$
, a marginal increase in the constant debt to finance the constant adaptation increases the capital stock. Conversely, if
$k_{ss}^3\gt k^o$
, a marginal increase in the constant debt to finance the constant adaptation increases the capital stock. Conversely, if
![]() $k_{ss}^3\lt k^o$
, debt decreases it. On the contrary, suppose
$k_{ss}^3\lt k^o$
, debt decreases it. On the contrary, suppose
![]() $v\gt \underline {v}$
,
$v\gt \underline {v}$
,
![]() $\Gamma _B(\hat {k_B})\lt \hat {k_B}$
, and
$\Gamma _B(\hat {k_B})\lt \hat {k_B}$
, and
![]() $k_{ss}^1\gt \underline {k_B}$
as in case (vi) of Proposition7. Then, steady-state capital stock
$k_{ss}^1\gt \underline {k_B}$
as in case (vi) of Proposition7. Then, steady-state capital stock
![]() $k_{ss}^1$
is locally stable. Suppose further that the economy lies on
$k_{ss}^1$
is locally stable. Suppose further that the economy lies on
![]() $k_{ss}=k_{ss}^1$
; if
$k_{ss}=k_{ss}^1$
; if
![]() $k_{ss}^1\lt k^o$
, the debt increases the capital stock. If
$k_{ss}^1\lt k^o$
, the debt increases the capital stock. If
![]() $k_{ss}^1\gt k^o$
, the debt decreases it.
$k_{ss}^1\gt k^o$
, the debt decreases it.
We can summarize the results thus far in the following corollary.
COROLLARY 3.
Suppose investment in adaptation and public debt are constant, and Assumptions1, 2, and 3 are satisfied. Then, the per capita capital stock at locally stable steady states,
![]() $k_{ss}$
, increases with debt if (i)
$k_{ss}$
, increases with debt if (i)
![]() $v\lt \underline {v}$
and
$v\lt \underline {v}$
and
![]() $k_{ss}^3\gt k^o$
or (ii)
$k_{ss}^3\gt k^o$
or (ii)
![]() $v\gt \underline {v}$
and
$v\gt \underline {v}$
and
![]() $k_{ss}^1\lt k^o$
.
$k_{ss}^1\lt k^o$
.
Corollary3 says that when
![]() $B$
is sufficiently low, the initial capital stocks tend to be characterized by under-accumulation in both cases (i) and (ii). Then, an increase in public debt
$B$
is sufficiently low, the initial capital stocks tend to be characterized by under-accumulation in both cases (i) and (ii). Then, an increase in public debt
![]() $B$
is welfare improving if it leads to an increase in the capital stock. When the government increases
$B$
is welfare improving if it leads to an increase in the capital stock. When the government increases
![]() $B$
and thereby the adaptation, there are two opposing effects on
$B$
and thereby the adaptation, there are two opposing effects on
![]() $k$
. Any improvement in adaptation should reduce the need for mitigation (substitution effect), and thus increase savings. At the same time, public debt is increasing, which could lead to a crowding-out effect and reduce capital accumulation. The main effects come through, on the one hand, the interest rate level which impacts the cost of debt repayment, and, on the other hand, the level of savings to satisfy consumption needs when retired. For low
$k$
. Any improvement in adaptation should reduce the need for mitigation (substitution effect), and thus increase savings. At the same time, public debt is increasing, which could lead to a crowding-out effect and reduce capital accumulation. The main effects come through, on the one hand, the interest rate level which impacts the cost of debt repayment, and, on the other hand, the level of savings to satisfy consumption needs when retired. For low
![]() $v$
and high
$v$
and high
![]() $k$
as Case (i), the interest rate and mitigation subsidies are low, which means that the increase in debt can finance a high amount of adaptation investments. Pollution has a lower welfare effect and private spending on mitigation is reduced. Conversely, for high
$k$
as Case (i), the interest rate and mitigation subsidies are low, which means that the increase in debt can finance a high amount of adaptation investments. Pollution has a lower welfare effect and private spending on mitigation is reduced. Conversely, for high
![]() $v$
and low
$v$
and low
![]() $k$
as Case (ii), pollution stock is low, and adaptation is high enough to fight its consequences on welfare.
$k$
as Case (ii), pollution stock is low, and adaptation is high enough to fight its consequences on welfare.
Case (ii) of Corollary3 requires the mitigation subsidy to be sufficiently high in low capital stock countries. By contrast, case (i) shows that sufficiently low subsidies is required in countries with high per capita capital stock. Therefore, when the government is indebted and the mitigation subsidy is low, financing public investment for mitigation or adaptation with public debt can be beneficial when the capital stock is high enough but is detrimental otherwise.
The debt policy is of great interest because it allows an optimal situation to be reached in terms of adaptation while sharing the cost of the policy between generations. The latter makes environmental policy more acceptable in the short term and under certain conditions, without compromising economic growth.
5.3. Public mitigation and private adaptation
Whether adaptation and mitigation are private or public is not obvious and may depend on the technologies, the scale, pollution characteristics for instance. To limit the number of cases, we have considered the case where adaptation is a public good, focusing on investments such as buildings, dikes, health and education spending. The converse is an alternative case where adaptation is a local and private decision, (i.e., an “individual choice”), such as cooling systems or crop diversification for a farmer in developing countries. Meanwhile, the government provides the mitigation services, for example, by building and operating carbon capture and storage (CCS) facilities. In this section, we consider the case where adaptation is endogenous and chosen by households, while the government decides on the level of mitigation spending.
An individual born at period
![]() $t$
invests part of her disposable income when young in adaptation services
$t$
invests part of her disposable income when young in adaptation services
![]() $h_{t}$
. The rest of income at
$h_{t}$
. The rest of income at
![]() $t$
is saved and consumed with an interest rate,
$t$
is saved and consumed with an interest rate,
![]() $R_{t+1}$
, when old. The private adaptation
$R_{t+1}$
, when old. The private adaptation
![]() $h_t$
is subsidized at a rate of
$h_t$
is subsidized at a rate of
![]() $v$
whereas the consumption is taxed at
$v$
whereas the consumption is taxed at
![]() $\tau ^{c}$
. Thus, the individual maximizes her lifetime utility (3) subject to the following intertemporal budget constraint:
$\tau ^{c}$
. Thus, the individual maximizes her lifetime utility (3) subject to the following intertemporal budget constraint:
With (67), the individual chooses the consumption at
![]() $t+1$
as
$t+1$
as
We assume that the mitigation services are fixed over time:
![]() $m_t=\bar {m}$
$m_t=\bar {m}$
![]() $\forall t$
. The government’s budget is balanced at each period:
$\forall t$
. The government’s budget is balanced at each period:
The capital market equilibrium writes:
![]() $k_{t+1}=s_t$
. By using (68), we obtain
$k_{t+1}=s_t$
. By using (68), we obtain
From (67), we can derive the adaptation investment,
![]() $h_t$
:
$h_t$
:
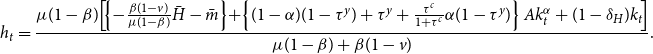 \begin{eqnarray} h_t=\frac {\mu (1-\beta)\!\left [\!\left \{-\frac {\beta (1-v)}{\mu (1-\beta)}\bar {H}-\bar {m}\right \}\!+ \!\left \{(1-\alpha)(1-\tau ^y)+\tau ^y+\frac {\tau ^c}{1+\tau ^c}\alpha (1-\tau ^y)\right \}Ak_t^\alpha +(1-\delta _H)k_t\!\right]}{\mu (1-\beta)+\beta (1-v)}.\!\! \notag\\ \end{eqnarray}
\begin{eqnarray} h_t=\frac {\mu (1-\beta)\!\left [\!\left \{-\frac {\beta (1-v)}{\mu (1-\beta)}\bar {H}-\bar {m}\right \}\!+ \!\left \{(1-\alpha)(1-\tau ^y)+\tau ^y+\frac {\tau ^c}{1+\tau ^c}\alpha (1-\tau ^y)\right \}Ak_t^\alpha +(1-\delta _H)k_t\!\right]}{\mu (1-\beta)+\beta (1-v)}.\!\! \notag\\ \end{eqnarray}
By using (71), we finally derive the dynamics of the capital accumulation (70) as
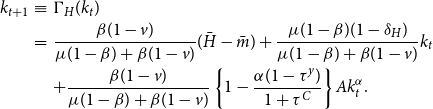 \begin{eqnarray} k_{t+1}&\equiv & \Gamma _H(k_t)\nonumber \\ &=&\frac {\beta (1-v)}{\mu (1-\beta)+\beta (1-v)}(\bar {H}-\bar {m}) +\frac {\mu (1-\beta)(1-\delta _H)}{\mu (1-\beta)+\beta (1-v)}k_t \nonumber \\ & & +\frac {\beta (1-v)}{\mu (1-\beta)+\beta (1-v)}\left \{ 1-\frac {\alpha (1-\tau ^y)}{1+\tau ^C} \right \}Ak_t^\alpha. \end{eqnarray}
\begin{eqnarray} k_{t+1}&\equiv & \Gamma _H(k_t)\nonumber \\ &=&\frac {\beta (1-v)}{\mu (1-\beta)+\beta (1-v)}(\bar {H}-\bar {m}) +\frac {\mu (1-\beta)(1-\delta _H)}{\mu (1-\beta)+\beta (1-v)}k_t \nonumber \\ & & +\frac {\beta (1-v)}{\mu (1-\beta)+\beta (1-v)}\left \{ 1-\frac {\alpha (1-\tau ^y)}{1+\tau ^C} \right \}Ak_t^\alpha. \end{eqnarray}
As previously shown, we define
![]() $\hat {k}_H$
such that
$\hat {k}_H$
such that
![]() $\Gamma _{H}^{\prime }(\hat {k}_H)=1$
, given as
$\Gamma _{H}^{\prime }(\hat {k}_H)=1$
, given as
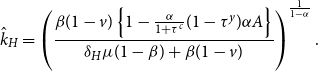 \begin{eqnarray} \hat {k}_H=\left (\frac {\beta (1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\alpha A \right \}}{\delta _H \mu (1-\beta)+\beta (1-v)}\right)^{\frac {1}{1-\alpha }}. \end{eqnarray}
\begin{eqnarray} \hat {k}_H=\left (\frac {\beta (1-v)\left \{ 1-\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\alpha A \right \}}{\delta _H \mu (1-\beta)+\beta (1-v)}\right)^{\frac {1}{1-\alpha }}. \end{eqnarray}
We then have the following cases.
PROPOSITION 8. Suppose that the government finances the adaptation while households provide the adaptation. The steady-state equilibria are characterized by the following cases.
-
(i) If
 $\bar {H}\gt \bar {m}$
, there exists a positive, unique, and stable steady state.
$\bar {H}\gt \bar {m}$
, there exists a positive, unique, and stable steady state.
-
(ii) If
 $\bar {H}=\bar {m}$
, there exist two steady states,
$\bar {H}=\bar {m}$
, there exist two steady states,
 $k_{ss}^1=0$
and
$k_{ss}^1=0$
and
 $k_{ss}^2\gt 0$
. Then,
$k_{ss}^2\gt 0$
. Then,
 $k_{ss}^1$
is unstable, whereas
$k_{ss}^1$
is unstable, whereas
 $k_{ss}^2$
is stable.
$k_{ss}^2$
is stable.
-
(iii) If
 $\bar {H}\lt \bar {m}$
and
$\bar {H}\lt \bar {m}$
and
 $ \Gamma _{H}^{\prime }(\hat {k}_H)\gt \hat {k}_H$
, there exist three steady states,
$ \Gamma _{H}^{\prime }(\hat {k}_H)\gt \hat {k}_H$
, there exist three steady states,
 $k_{ss}^1=0$
,
$k_{ss}^1=0$
,
 $0\lt k_{ss}^{2}\lt k_{ss}^3$
. Then,
$0\lt k_{ss}^{2}\lt k_{ss}^3$
. Then,
 $k_{ss}^{1}$
is locally stable,
$k_{ss}^{1}$
is locally stable,
 $k_{ss}^{2}$
unstable, and
$k_{ss}^{2}$
unstable, and
 $k_{SS}^{3}$
is positive and locally stable.
$k_{SS}^{3}$
is positive and locally stable.
-
(iv)
 $\bar {H}\lt \bar {m}$
and
$\bar {H}\lt \bar {m}$
and
 $ \Gamma _{H}^{\prime }(\hat {k}_H)=\hat {k}_H$
, there exist two steady states,
$ \Gamma _{H}^{\prime }(\hat {k}_H)=\hat {k}_H$
, there exist two steady states,
 $k_{ss}^{1}=0$
and
$k_{ss}^{1}=0$
and
 $k_{ss}^{2}\gt 0$
. Then,
$k_{ss}^{2}\gt 0$
. Then,
 $k_{ss}^{1}$
is locally stable, whereas
$k_{ss}^{1}$
is locally stable, whereas
 $k_{ss}^{2}$
is unstable (one-side stable).
$k_{ss}^{2}$
is unstable (one-side stable).
-
(v)
 $\bar {H}\lt \bar {m}$
and
$\bar {H}\lt \bar {m}$
and
 $ \Gamma _{H}^{\prime }(\hat {k}_H)\lt \hat {k}_H$
there exists a unique and stable steady state,
$ \Gamma _{H}^{\prime }(\hat {k}_H)\lt \hat {k}_H$
there exists a unique and stable steady state,
 $k_{ss}^{1}=0$
.
$k_{ss}^{1}=0$
.
Proof. See Appendix F.
When mitigation is provided by the government, its size relative to natural adaptation is key to determining the characteristics of the steady state. As public investment in abatement crowds out capital accumulation, the dynamics of capital shown in (72) shifts downward and modifies the steady states.
Then, are the public mitigation and private adaptation complementary? To answer this question, we first derive how the capital stock is affected by an increase in the mitigation from (72) at the stable steady state.
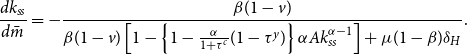 \begin{eqnarray} \frac {dk_{ss}}{d\bar {m}}=-\frac {\beta (1-v)}{\beta (1-v)\left [1-\left \{1-\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\right \}\alpha A k_{ss}^{\alpha -1} \right]+\mu (1-\beta)\delta _H}. \end{eqnarray}
\begin{eqnarray} \frac {dk_{ss}}{d\bar {m}}=-\frac {\beta (1-v)}{\beta (1-v)\left [1-\left \{1-\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\right \}\alpha A k_{ss}^{\alpha -1} \right]+\mu (1-\beta)\delta _H}. \end{eqnarray}
The mitigation increases
![]() $k_{ss}$
when the capital stock is sufficiently small but decreases
$k_{ss}$
when the capital stock is sufficiently small but decreases
![]() $k_{ss}$
when it is large enough. For more detail, we substitute
$k_{ss}$
when it is large enough. For more detail, we substitute
![]() $k_{ss}=\hat {k}_H$
of (73) into (74). Then, the denominator of (74) turns to
$k_{ss}=\hat {k}_H$
of (73) into (74). Then, the denominator of (74) turns to
![]() $0$
. As the capital stock approaches to
$0$
. As the capital stock approaches to
![]() $\hat {k}_H$
from
$\hat {k}_H$
from
![]() $0$
,
$0$
,
![]() $\frac {dk_{ss}}{d\bar {m}}$
diverges to
$\frac {dk_{ss}}{d\bar {m}}$
diverges to
![]() $+\infty$
. From Proposition8 and Appendix F, the capital stock at the stable steady states is greater than
$+\infty$
. From Proposition8 and Appendix F, the capital stock at the stable steady states is greater than
![]() $\hat {k}_H$
. Therefore, at the stable steady states, we always have
$\hat {k}_H$
. Therefore, at the stable steady states, we always have
![]() $\frac {dk_{ss}}{d\bar {m}}\lt 0$
.
$\frac {dk_{ss}}{d\bar {m}}\lt 0$
.
Second, we derive a total derivative of
![]() $h_{ss}$
and
$h_{ss}$
and
![]() $\bar {m}$
in (71) and obtain the following:
$\bar {m}$
in (71) and obtain the following:
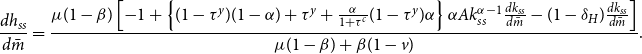 \begin{eqnarray} \frac {dh_{ss}}{d\bar {m}}=\frac {\mu (1-\beta)\left [-1+\left \{(1-\tau ^y)(1-\alpha)+\tau ^y+\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\alpha \right \}\alpha A k_{ss}^{\alpha -1}\frac {dk_{ss}}{d\bar {m}}-(1-\delta _H)\frac {dk_{ss}}{d\bar {m}} \right] }{\mu (1-\beta)+\beta (1-v)}. \notag\\ \end{eqnarray}
\begin{eqnarray} \frac {dh_{ss}}{d\bar {m}}=\frac {\mu (1-\beta)\left [-1+\left \{(1-\tau ^y)(1-\alpha)+\tau ^y+\frac {\alpha }{1+\tau ^c}(1-\tau ^y)\alpha \right \}\alpha A k_{ss}^{\alpha -1}\frac {dk_{ss}}{d\bar {m}}-(1-\delta _H)\frac {dk_{ss}}{d\bar {m}} \right] }{\mu (1-\beta)+\beta (1-v)}. \notag\\ \end{eqnarray}
From this expression, since the third term in square brackets on the numerator is positive (
![]() $-(1-\delta _H)\frac {dk_{ss}}{d\bar {m}}\gt 0$
), the adaptation may increase when
$-(1-\delta _H)\frac {dk_{ss}}{d\bar {m}}\gt 0$
), the adaptation may increase when
![]() $k_{ss}$
is large enough. However, we have
$k_{ss}$
is large enough. However, we have
![]() $\lim _{k_{ss}\rightarrow +\infty }\frac {dk_{ss}}{d\bar {m}}=-\frac {\beta (1-v)}{\beta (1-v)+\mu (1-\beta)\delta _H}$
from (74), and thereby
$\lim _{k_{ss}\rightarrow +\infty }\frac {dk_{ss}}{d\bar {m}}=-\frac {\beta (1-v)}{\beta (1-v)+\mu (1-\beta)\delta _H}$
from (74), and thereby
![]() $\lim _{k_{ss}\rightarrow +\infty } \frac {dh_{ss}}{d\bar {m}}=-\frac {\mu (1-\beta)\delta _H}{\beta (1-v)+\mu (1-\beta)\delta _H}\lt 0$
from (75). Discussion so far provides the following proposition.
$\lim _{k_{ss}\rightarrow +\infty } \frac {dh_{ss}}{d\bar {m}}=-\frac {\mu (1-\beta)\delta _H}{\beta (1-v)+\mu (1-\beta)\delta _H}\lt 0$
from (75). Discussion so far provides the following proposition.
PROPOSITION 9. Suppose that adaptation is provided by households and mitigation is provided by the government. Then, mitigation and adaptation are substitutes for all stable steady states.
Whether adaptation and mitigation are complements or substitutes depends not only on the level of the capital stock and the policy instruments (propositions3 and 6), but also on who provides what (Proposition9). Public mitigation directly crowds out private adaptation as a substitution effect. Although savings and thus the capital stock could be increased instead, the steady-state capital stock does not increase from (74). This implies that the government intervention is so large that the income effect from the increased mitigation is negative for private adaptation.
6. Conclusion
This study examines the interactions between adaptation, mitigation, and fiscal policies. Adaptation comprises public infrastructure financed by tax revenue and public debt, whereas mitigation is a private decision supported by subsidies. Pollution results from household consumption, but its welfare consequences are limited by adaptation investment. To consider these features, we study the dynamics of capital in an overlapping generation model. Fiscal policy has a twofold effect on households’ budget constraints through taxation for financing public adaptation and through subsidies for private mitigation. First, we find that it is possible to explicitly determine a policy to decentralize the optimal solution. This policy requires setting tax rates on consumption and production, subsidies for mitigation, and public spending on adaptation at specific levels, which depend on both environmental parameters (pollution rate) and economic development (capital stock). We also show that adaptation and mitigation may be substitutes or complements depending on the level of economic development, but also on the level of mitigation subsidy. Finally, when the government is indebted, we show that financing public adaptation and/or subsidizing private mitigation through an increase in public debt could be beneficial for countries with high capital stock, but is detrimental when the capital stock is too low.
Our results can easily be extended by considering the government’s exogenous mitigation investment at the optimal level, for example, in addition to public investment in adaptation infrastructure. In this case, the government has a direct instrument (mitigation) and no longer needs to provide incentives to households for mitigation. Moreover, our results remain valid when the decision to invest in an adaptation stock becomes private, instead of mitigation. However, in our framework, the consequences of adaptation concern households’ welfare; it neglects the direct consequences on biodiversity and animal welfare, and to a lesser extent, the indirect effects on the environment (as only consumption is a source of pollution). Therefore, the consequences of adaptation are likely to be underestimated. Finally, we assume homogeneity of the agents within each generation. It would be interesting to extend this model to heterogeneous agents whose contributions to mitigation would be different. Depending on the form of the utility function, the adaptation needs would also be different, which would have a significant effect on equilibrium and the definition of efficient policy tools in the absence of coordination.
In this paper, we focus on stable steady-states in order to analyze long-term consequences of environmental policies on pollution and public finance. Note that our comparative statics refers to locally stable steady states, but our figures allow for a global stability analysis. Our complete analysis of paths and equilibria allows us to determine the conditions for unicity and stability. Nevertheless, our results show that cycles and bifurcations can emerge for some specific policy parameters. A detailed analysis of these complex dynamics need to be carried out in future works.
Further issues to be considered are uncertainty and/or a tipping point of climate change.Footnote 6 Indeed, the environmental damage caused by climate change could be subject to uncertainty. We expect that not only optimal policies but also the substitutability between mitigation and adaptation will be affected by the probabilistic features of climate change. Finally, further extensions could include considering other sources of pollution (such as fossil energy or production) instead of consumption, as well as changes in production technologies. These issues are thus significant and therefore to be analyzed in future works.
Supplementary material
To view supplementary material for this article, please visit https://10.1017/S1365100525000252
Acknowledgements
This paper was presented at seminars of Univ. Paris Ouest Nanterre, ETH Zurich, Montpellier, Nantes, and Seikei, and conferences of EENR at Univ. Orléans (2022) and PET (2022) at Aix-Marseille School of Econ. The authors are grateful to participants of seminars and conferences, along with two anonymous referees from this journal, for their valuable feedback that improved this paper. Hiroaki Yamagami is grateful for the research grant from Seikei University and JSPS Grant-in-Aid for Scientific Research (C) (No. 21K01489).







