Hostname: page-component-5b777bbd6c-cp4x8 Total loading time: 0 Render date: 2025-06-23T16:21:33.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On HAP triangles

Published online by Cambridge University Press:  20 June 2025

Emrys Read
Emrys Read*
Affiliation:
5 Cefn Cynrig, Bethel, Caernarfon, LL55 1UW e-mail: mairacemrys@btinternet.com
Get access Rights & Permissions [Opens in a new window]

Extract

It is a well known and easily verifiable fact that not all integer triangles have integer areas. Consider the triangles with sides {9, 10, 17}, {13, 14, 15}, {5, 7, 8} and {6, 7, 9} with respective areas 36, 84, 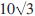and 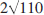. The first two, whose areas are integers, are called Heronian triangles. The second triangle also has the additional property that its sides are consecutive integers and is an example of a Brahmagupta triangle, named after an Indian mathematician, born in AD 598. These are called Super-Heronian triangles in [1] and a method is developed there for generating examples of such triangles.

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 294 - 302
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Richardson, William H., Super-Heronian triangles (2010), available at https://www.math.wichita.edu/~richardson/heronian/heronian.html Google Scholar
MacDougall, J. A, Heron triangles with sides in arithmetic progression, Jour. Rec. Math. 31 (2003) pp. 189–196.Google Scholar
Bailey, Herb and Gosnell, William, Heronian triangles with sides in arithmetic progression: an inradius perspective, Maths Magazine, 85 (October 2012) pp. 290–294.CrossRefGoogle Scholar
Read, Emrys, On the class of an integer triangle, Math. Gaz. 106 (July 2022) pp. 291–299.Google Scholar
Read, Emrys, Heronian triangles, Math. Gaz. 100 (March 2016) pp. 103–108.Google Scholar