Hostname: page-component-5b777bbd6c-5mwv9 Total loading time: 0 Render date: 2025-06-23T05:31:44.732Z Has data issue: false hasContentIssue false
  • English
  • Français

Measures of unequilaterality and refinements of inequalities

Published online by Cambridge University Press:  20 June 2025

Martin Lukarevski  and
Dan Stefan Marinescu
Martin Lukarevski
Affiliation:
Department of Mathematics and Statistics, University “Goce Delcev”, Stip, North Macedonia e-mail: martin.lukarevski@ugd.edu.mk
Dan Stefan Marinescu
Affiliation:
Colegiul National “Iancu De Hunedoara”, Hunedoara, Romania e-mail: marinescuds@gmail.com
Get access Rights & Permissions [Opens in a new window]

Extract

Let ABC be a triangle with sides a, b, c, semiperimeter s, circumradius R, inradius r and area Δ. We introduce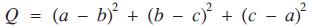

$$Q\, = \,{(a - b)^2}\, + \,{(b - c)^2}\, + \,{(c - a)^2}$$
and
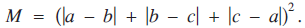$$M\, = \,{(\left| {a - b} \right|\, + \left| {b - c} \right|\, + \,\left| {c - a} \right|)^2}.$$

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 281 - 285
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Finsler, P., Hadwiger, H., Einige Relationen im Dreieck, Commentarii Mathematici Helvetici 10 (1937), pp. 316–326.CrossRefGoogle Scholar
Lukarevski, M., Wanner, G., Mixtilinear radii and Finsler-Hadwiger inequality, Elem. Math. 75(3) (2020) pp. 121–124.CrossRefGoogle Scholar
Lukarevski, M., Exarc radii and the Finsler-Hadwiger inequality, Math Gaz 106 (March 2022) pp. 138–143.CrossRefGoogle Scholar
Lukarevski, M., Exradii of the triangle and Euler’s inequality, Math. Gaz. 101 (March 2017) p. 123.CrossRefGoogle Scholar
Lukarevski, M., Problem 11938, Amer. Math. Monthly, 123(9) (2016).Google Scholar
Lukarevski, M., A simple proof of Kooi’s inequality, Math. Mag. 93, (2020) p. 225.CrossRefGoogle Scholar
Lukarevski, M., Marinescu, D. S., A refinement of the Kooi’s inequality, Mittenpunkt and applications, J. Inequal. Appl. 13 (2019) pp. 827–832.Google Scholar
Lukarevski, M., A new look at the fundamental triangle inequality, Math. Mag. 96 (2023) pp. 141–149.CrossRefGoogle Scholar
Ionescu, I., Problem 273, Romanian Mathematical Gazette, 13 (1897) p. 52.Google Scholar
Weitzenböck, R., Über eine Ungleichung in der Dreiecksgeometrie, Math. Zeitschr, 5 (1919) pp. 137–146.CrossRefGoogle Scholar
Lukarevski, M., The excentral triangle and a curious application to inequalities, Math. Gaz. 102 (November 2018) pp. 531–533.CrossRefGoogle Scholar
Lukarevski, M., The circummidarc triangle and the Finsler-Hadwiger inequality, Math. Gaz. 104 (July 2020) pp. 335–338.CrossRefGoogle Scholar
Minculete, N., Problem 11990, Amer. Math. Monthly, 124 (2017).Google Scholar
Lukarevski, M., An alternate proof of Gerretsen’s inequalities, Elem. Math. 72 (2017) pp. 2–8 CrossRefGoogle Scholar
Lukarevski, M., An inequality for the altitudes of the excentral triangle, Math. Gaz. 104 (March 2020) pp. 161–164.CrossRefGoogle Scholar
Bottema, O., Djordjevic, R. Z., Janic, R. R., Mitrinovic, D. S., Vasic, P. M., Geometric inequalities, Wolters-Noordhoff (1969).Google Scholar
Hungerbühler, N., Proof without words: the triangle of medians has three-fourths the area of the original triangle. Math. Mag. 72 (1999) p. 142.CrossRefGoogle Scholar
Stanean, M., Problem S609, Mathematical Reflections 6 (2022).Google Scholar
Lukarevski, M., Wolstenholme’s inequality and its relation to the Barrow and Garfunkel-Bankoff inequalities, Math. Gaz. 107 (March 2023) pp. 70–75.CrossRefGoogle Scholar