In the literature we find several different ways of introducing elementary functions. For the exponential function, we mention the following ways of characterising the exponential function:
(a) 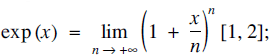
(b) 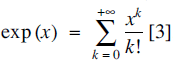 , also for complex values of x;
, also for complex values of x;
(c) x → exp (x) is the unique solution to the initial value problem [4]
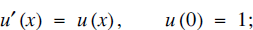
(d) x → exp (x) is the inverse of 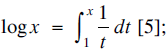
(e)x → exp (x) is the unique continuous function satisfying the
functional equation f (x + y) = f (x) f (y) and f(0) = 1 [6]; the corresponding definition is done for the logarithm in [7];
(f) Define dr for rational r, and then use a continuity/density argument [8].
All of them have their advantages and disadvantages. We like (a) and (c), mostly because they have natural interpretations, (a) in the setting of compound interest and (c) being a simple model of many processes in physics and other sciences, but also because they are related to methods and ideas that are (usually) introduced rather early to the students.
 ?
?