No CrossRef data available.
Article contents
Spectral Properties of Schrödinger-type Operators andLarge-time Behavior of the Solutions to the Corresponding Wave Equation
Published online by Cambridge University Press: 28 January 2013
Abstract
Let L be a linear, closed, densely defined in a Hilbert space operator,not necessarily selfadjoint. Consider the corresponding wave equations
\begin{eqnarray} &(1) \quad \ddot{w}+ Lw=0, \quadw(0)=0,\quad \dot{w}(0)=f, \quad \dot{w}=\frac{dw}{dt}, \quad f \in H. \\ &(2)\quad \ddot{u}+Lu=f e^{-ikt}, \quad u(0)=0, \quad \dot{u}(0)=0,\end{eqnarray}
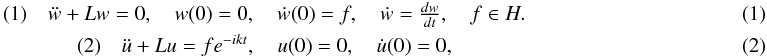(1) ¨w+Lw=0, w(0)=0, ẇ(0)=f, ẇ=dwdt, f∈H.(2) ¨u+Lu=fe−ikt, u(0)=0, u̇(0)=0,
where k > 0 is a constant. Necessary and sufficient conditions aregiven for the operator L not to have eigenvalues in the half-planeRez < 0 and not to have a positive eigenvalue at a given point kd2 > 0. These conditions are given in terms of the large-timebehavior of the solutions to problem (1) for generic f.
Sufficient conditions are given for the validity of a version of the limiting amplitudeprinciple for the operator L.
A relation between the limiting amplitude principle and the limiting absorption principleis established.
Information
- Type
- Research Article
- Information
- Mathematical Modelling of Natural Phenomena , Volume 8 , Issue 1: Harmonic analysis , 2013 , pp. 207 - 214
- Copyright
- © EDP Sciences, 2013
References
Eidus, D.. The limiting amplitude principle. Russ. Math. Surveys, 24, (1969), 51–94
CrossRefGoogle Scholar
D. Pearson. Quantum scattering and spectral theory. Acad. Press, London, 1988.
Ramm, A.G.. Spectral properties of the Schrödinger operator in some domains with infinite boundaries. Doklady Acad of Sci. USSR, 152, (1963) 282-285. Google Scholar
Ramm, A.G.. Spectral properties of the Schrödinger operator in some infinite domains. Mat. Sborn., 66, (1965), 321-343. Google Scholar
Ramm, A.G.. Sufficient conditions for zero not to be an eigenvalue of the Schrödinger operator. J. Math. Phys., 28, (1987), 1341–1343. CrossRefGoogle Scholar
Ramm, A.G.. Conditions for zero not to be an eigenvalue of the Schrödinger operator. J. Math. Phys. 29, (1988), 1431–1432. CrossRefGoogle Scholar
Ramm, A.G.. Eigenfunction expansion for nonselfadjoint Schrödinger operator. Doklady Acad. Sci. USSR. 191, (1970), 50-53. Google Scholar
A.G. Ramm. Scattering by obstacles. D. Reidel, Dordrecht, 1986.
Ramm, A.G..Stability of solutions to some evolution problems. Chaotic Modeling and Simulation (CMSIM), 1, (2011), 17-27. Google Scholar
A.G. Ramm. Inverse problems. Springer, New York, 2005.
M. Schechter. Operator methods in quantum mechanics. North Holland, New York, 1981.