Hostname: page-component-594f858ff7-c4bbg Total loading time: 0 Render date: 2023-06-08T13:01:38.401Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "corePageComponentUseShareaholicInsteadOfAddThis": true, "coreDisableSocialShare": false, "useRatesEcommerce": true } hasContentIssue false
  • English

Cohomology with coefficients in symmetric cat-groups. An extension of Eilenberg–MacLane's classification theorem

Published online by Cambridge University Press:  24 October 2008

M. Bullejos ,
P. Carrasco  and
A. M. Cegarra
M. Bullejos
Affiliation:
Departamento de Algebra, Universidad de Granada, 18071 Granada, Spain
P. Carrasco
Affiliation:
Departamento de Algebra, Universidad de Granada, 18071 Granada, Spain
A. M. Cegarra
Affiliation:
Departamento de Algebra, Universidad de Granada, 18071 Granada, Spain
Get access Rights & Permissions[Opens in a new window]

Abstract

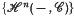In this paper we use Takeuchy–Ulbrich's cohomology of complexes of categories with abelian group structure to introduce a cohomology theory for simplicial sets, or topological spaces, with coefficients in symmetric cat-groups 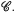. This cohomology is the usual one when abelian groups are taken as coefficients, and the main topological significance of this cohomology is the fact that it is equivalent to the reduced cohomology theory defined by a Ω-spectrum, {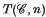}, canonically associated to 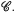. We use the spaces 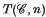to prove that symmetric cat-groups model all homotopy type of spaces X with Πi(X) = 0 for all i ╪ n, n + 1 and n ≥ 3, and then we extend Eilenberg–MacLane's classification theorem to those spaces: .

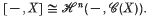Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 114 , Issue 1 , July 1993 , pp. 163 - 189
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baues, H. J.. Obstruction Theory. Lecture Notes in Math. vol. 628 (Springer-Verlag, 1977).Google Scholar
[2]Baues, H. J.. Moore Spaces, preprint.Google Scholar
[3]Brown, R. and Gilbert, N. D.. Algebraic models of 3-types and automorphism structures for crossed modules. Proc. London Math. Soc. (2) 59 (1989), 51–73.CrossRefGoogle Scholar
[4]Brown, R. and Higgins, P. J.. The classifying space of a crossed complex. Math. Proc. Cambridge Phil. Soc. 110 (1991), 95–120.CrossRefGoogle Scholar
[5]Bullejos, M. and Cegarra, A. M.. A 3-dimensional non-abelian cohomology with applications to homotopy classification of continuous maps. Canadian Journal of Mathematics (2) 43 (1991), 265–296.CrossRefGoogle Scholar
[6]Bullejos, M., Cegarra, A. M. and Duskin, J.. On catn-groups and homogopy types. To appear in Journal of Pure and Applied Algebra (1993).CrossRefGoogle Scholar
[7]Carrasco, P. and Cegarra, A. M.. Group theoretic algebraic models for homotopy types. Journal of Pure and Applied Algebra 75 (1991), 195–235.CrossRefGoogle Scholar
[8]Cegarra, A. M., Bullejos, M. and Garzón, A. R.. Higher dimensional obstruction theory in algebraic categories. Journal of Pure and Applied Algebra 49 (1987), 43–102.CrossRefGoogle Scholar
[9]Conduché, D.. Modules croisés generalisés de longueur 2. Journal of Pure and Applied Algebra 34 (1984), 155–178.CrossRefGoogle Scholar
[10]Dedecker, P.. Cohomologie non-abélienne. (Mimeographie, Fac. Sc. Lille, 1965.)Google Scholar
[11]Duskin, J.. Simplicial methods and the interpretation of triple cohomology. Memoirs Amer. Math. Soc. vol. 3, issue 2, no. 163 (1975).CrossRefGoogle Scholar
[12]Eilenberg, S. and Kelly, G. M.. Closed categories. Proc. of the Conference on Categorical Algebra at La JollaSpringer-Verlag, 1965), 421–562.Google Scholar
[13]Eilenberg, S. and MacLane, S.. On the groups H(π, n) I, II and III. Annals of Math. 58 (1953), 55–106; 70 (1954), 49–137; 60 (1954), 513–557.CrossRefGoogle Scholar
[14]Epstein, D. B. A.. Functors between tensored categories. Invent. Math. 1 (1966), 221–228.CrossRefGoogle Scholar
[15]Frölich, A. and Wall, C. T. C.. Graded monoidal categories. Compositio Mathematica (3) 28 (1974), 229–285.Google Scholar
[16]Joyal, A. and Street, R.. Braided tensor categories. Advances in Math. (1) 82 (1991).Google Scholar
[17]Loday, J. L.. Spaces with finitely many non-trivial homotopy groups. Journal of Pure and Applied Algebra 24 (1982), 179–202.CrossRefGoogle Scholar
[18]MacLane, S.. Categories for the working mathematician. (Graduate Texts in Math. 5, Springer-Verlag, 1971.)Google Scholar
[19]MacLane, S.. Natural associativity and commutativity. Rice University Studies 49 (1963), 28–46. (Sanders MacLane selected papers (Springer-Verlag, 1979), pp. 415–433.)Google Scholar
[20]MacLane, S. and Whitehead, J. H. C.. On the 3-type of a complex. Proc. Acad. U.S.A. 30 (1956), 41–48.Google Scholar
[21]May, J. P.. Simplicial objects in algebraic topology (Van Nostrand, 1976).Google Scholar
[22]Moore, J. C.. Seminar on algebraic homotopy theory (Princeton, 1956).Google Scholar
[23]Takeuchi, M. and Ulbrich, K. H.. Complexes of categories with abelian group structure. Journal of Pure and Applied Algebra 27 (1983), 61–73.CrossRefGoogle Scholar
[24]Ulbrich, K. H.. Group cohomology for Picard categories. Journal of Algebra 91 (1984), 464–498.CrossRefGoogle Scholar
[25]Ulbrich, K. H.. Kohärenz in kategorien mit Gruppenstruktur I, II and III. Journal of Algebra 78 (1981), 279–295; 81 (1983), 279–294; 88 (1984), 292–316.CrossRefGoogle Scholar
[26]Whitehead, G. W.. Elements of homotopy theory (Graduate Texts in Math. Springer 61, 1978).CrossRefGoogle Scholar
[27]Whitehead, J. H. C.. Combinatorial homotopy I and II. Bulletin A.M.S. 55 (1949), 213–245, 496–543.CrossRefGoogle Scholar