Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-17T07:20:36.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of Jacobian manifolds and characteristic classes of surface bundles. II

Published online by Cambridge University Press:  24 October 2008

Shigeyuki Morita
Shigeyuki Morita
Affiliation:
Department of Mathematics, Faculty of Science, Tokyo Institute of Technology, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let Σg be a closed orientable surface of genus g, which will be assumed to be greater than one throughout this paper. In our previous paper [11], we have associated to any oriented ∑g-bundle π: E → X with a cross-section s: X → E a flat T2g-bundle π: J → X and a fibre-preserving embedding j: E → J such that the restriction of j to any fibre Ep = π−1(p)(p ∈ X) is equivalent to the Jacobi mapping of Ep with respect to some conformal structure on it and relative to the base-point s(p) ∈ Ep. There is a canonical oriented S1-bundle over J and the main result of [11] is the identification of the Euler class of the pullback of this S1-bundle by the map j as an element of H2(E, ). 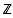In this paper we deal with the case of Σg-bundles without cross-sections. First of all we associate a flat T2g-bundle π′: J′ → X to any oriented Σg-bundle π: E → X and construct a fibre-preserving embedding j′: E → J′ such that the restriction of j′ to any fibre Ep is equivalent to some translation of the Jacobi mapping of it. Although our original motivation for the present work came from a different source, this should be considered as a topological version of Earle's embedding theorem [5] which states that any holomorphic family of compact Riemann surfaces over a complex manifold can be embedded in a certain associated family of the corresponding Jacobian varieties in an essentially unique way.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 79 - 101
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F.. The signature of fibre-bundles. In Global Analysis, Papers in Honor of K. Kodaira (University of Tokyo Press, 1969), pp. 73–84.Google Scholar
[2]Bott, R.. Some remarks on continuous cohomology. In Manifolds Tokyo 1973 (University of Tokyo Press, 1975), pp. 161–170.Google Scholar
[3]Brown, K. S.. Cohomology of Groups. Graduate Texts in Math. no. 87 (Springer-Verlag, 1982).CrossRefGoogle Scholar
[4]Chillingworth, C. J.. Winding numbers on surfaces II. Math. Ann. 199 (1972), 131–153.CrossRefGoogle Scholar
[5]Earle, C. J.. Families of Riemann surfaces and Jacobi varieties. Ann. of Math. (2) 107 (1978), 255–286.CrossRefGoogle Scholar
[6]Harris, J.. Families of smooth curves. Duke Math. J. 51 (1984), 409–419.CrossRefGoogle Scholar
[7]Johnson, D.. Homeomorphisms of a surface which act trivially on homology. Proc. Amer. Math. Soc. 75 (1979), 119–125.CrossRefGoogle Scholar
[8]Johnson, D.. An abelian quotient of the mapping class group lg. Math. Ann. 249 (1980), 225–242.CrossRefGoogle Scholar
[9]Miller, E. Y.. The homology of the mapping class group. J. Differential Geom. 24 (1986), 1–14.CrossRefGoogle Scholar
[10]Morita, S.. Characteristic classes of surface bundles. Invent. Math. 90 (1987), 551–577.CrossRefGoogle Scholar
[11]Morita, S.. Families of Jacobian manifolds and characteristic classes of surface bundles I. (Preprint.)Google Scholar
[12]Morita, S.. Family of Jacobian manifolds and characteristic classes of surface bundles II. Proc. Japan Acad. Ser. A Math. Sci. 61 (1985), 112–115.CrossRefGoogle Scholar
[13]Morita, S.. The second homology group of the mapping class groups of orientable surfaces with twisted coefficients. (In preparation.)Google Scholar
[14]Morita, S.. Casson's invariant for homology 3-spheres and characteristic classes of surface bundles I. (Preprint.)Google Scholar
[15]Mumford, D.. Towards an enumerative geometry of the moduli space of curves. In Arithmetic and Geometry, Progress in Math. no. 36 (Birkhäuser-Verlag, 1983), pp. 271–328.CrossRefGoogle Scholar