Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lozano, María Teresa
1987.
Constructions of arcbodies.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 1,
p.
79.
Kojima, S.
and
Long, D.D.
1988.
A Fête of Topology.
p.
417.
Lozano, María Teresa
and
Safont, Carmen
1989.
Virtually regular coverings.
Proceedings of the American Mathematical Society,
Vol. 106,
Issue. 1,
p.
207.
Menasco, William
and
Reid, Alan W.
1992.
Topology '90.
p.
215.
Adams, Colin C.
and
Reid, Alan W.
1993.
Quasi-Fuchsian surfaces in hyperbolic knot complements.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 55,
Issue. 1,
p.
116.
Maclachlan, C.
and
Reid, A. W.
1997.
Generalised Fibonacci manifolds.
Transformation Groups,
Vol. 2,
Issue. 2,
p.
165.
Finkelstein, Elizabeth
and
Moriah, Yoav
1999.
Closed incompressible surfaces in knot complements.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 2,
p.
655.
Ichihara, Kazuhiro
and
Ozawa, Makoto
2000.
Hyperbolic knot complements without closed embedded totally geodesic surfaces.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 68,
Issue. 3,
p.
379.
Scannell, Kevin P.
2000.
Infinitesimal deformations of some SO(3,1) lattices.
Pacific Journal of Mathematics,
Vol. 194,
Issue. 2,
p.
455.
Matsuda, Hiroshi
2002.
Complements of hyperbolic knots of braid index four contain no closed embedded totally geodesic surfaces.
Topology and its Applications,
Vol. 119,
Issue. 1,
p.
1.
Scannell, Kevin P.
2002.
Local rigidity of hyperbolic 3-manifolds after Dehn surgery.
Duke Mathematical Journal,
Vol. 114,
Issue. 1,
Adams, Colin
and
Schoenfeld, Eric
2005.
Totally Geodesic Seifert Surfaces in Hyperbolic Knot and Link Complements I.
Geometriae Dedicata,
Vol. 116,
Issue. 1,
p.
237.
DeBlois, Jason
2006.
Totally geodesic surfaces and homology.
Algebraic & Geometric Topology,
Vol. 6,
Issue. 3,
p.
1413.
Eudave-Muñoz, Mario
and
Ramírez-Losada, Enrique
2008.
Meridional surfaces and (1,1)-knots.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 2,
p.
671.
BIRMAN, JOAN S.
and
MENASCO, WILLIAM W.
2008.
A NOTE ON CLOSED 3-BRAIDS.
Communications in Contemporary Mathematics,
Vol. 10,
Issue. supp01,
p.
1033.
Futer, D.
Kalfagianni, E.
and
Purcell, J. S.
2010.
Cusp Areas of Farey Manifolds and Applications to Knot Theory.
International Mathematics Research Notices,
Ozawa, Makoto
2010.
Waist and trunk of knots.
Geometriae Dedicata,
Vol. 149,
Issue. 1,
p.
85.
KIM, TAEHEE
KITAYAMA, TAKAHIRO
and
MORIFUJI, TAKAYUKI
2013.
TWISTED ALEXANDER POLYNOMIALS ON CURVES IN CHARACTER VARIETIES OF KNOT GROUPS.
International Journal of Mathematics,
Vol. 24,
Issue. 03,
p.
1350022.
Nogueira, João Miguel
2015.
Prime knot complements with meridional essential surfaces of arbitrarily high genus.
Topology and its Applications,
Vol. 194,
Issue. ,
p.
427.
Przytycki, Józef H.
2019.
Nonorientable, incompressible surfaces in punctured-torus bundles over
$$S^1$$
S
1
.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 3,
p.
1975.


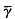 be a closed 3-braid in
be a closed 3-braid in 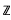 ) and the braid γ
) and the braid γ