Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ogden, R. W.
1974.
On isotropic tensors and elastic moduli.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 75,
Issue. 3,
p.
427.
Power, E. A.
and
Thirunamachandran, T.
1974.
Circular dichroism: A general theory based on quantum electrodynamics.
The Journal of Chemical Physics,
Vol. 60,
Issue. 9,
p.
3695.
Adu-Gyamfi, D.
and
Felderhof, B.U.
1975.
On the propagation of light in media with higher multipole densities.
Physica A: Statistical Mechanics and its Applications,
Vol. 81,
Issue. 2,
p.
295.
Healy, W P
1975.
On the isotropic averaging of fifth-order cartesian tensors.
Journal of Physics A: Mathematical and General,
Vol. 8,
Issue. 9,
p.
L87.
Andrews, D. L.
and
Thirunamachandran, T.
1977.
On three-dimensional rotational averages.
The Journal of Chemical Physics,
Vol. 67,
Issue. 11,
p.
5026.
Adu-Gyamfi, D.
1978.
On the electric quadrupole density of an isotropic non-polar fluid.
Physica A: Statistical Mechanics and its Applications,
Vol. 93,
Issue. 3-4,
p.
553.
Andrews, D. L.
and
Ghoul, W. A.
1982.
Irreducible fourth-rank Cartesian tensors.
Physical Review A,
Vol. 25,
Issue. 5,
p.
2647.
Appleby, P. G.
Duffy, B. R.
and
Ogden, R. W.
1987.
On the classification of isotropic tensors.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 2,
p.
185.
Andrews, David L.
and
Blake, Nick P.
1988.
Laser-induced molecular orientation effects in vibrational resonance-Raman spectroscopy.
Chemical Physics,
Vol. 122,
Issue. 2,
p.
169.
Ruchon, T.
Vallet, M.
Chauvat, D.
and
Le Floch, A.
2006.
A dipole interaction model for magnetochiral birefringence.
The Journal of Chemical Physics,
Vol. 125,
Issue. 8,
Jespersen, Sune Nørhøj
2012.
Equivalence of double and single wave vector diffusion contrast at low diffusion weighting.
NMR in Biomedicine,
Vol. 25,
Issue. 6,
p.
813.
Jespersen, Sune Nørhøj
Lundell, Henrik
Sønderby, Casper Kaae
and
Dyrby, Tim B.
2013.
Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments.
NMR in Biomedicine,
Vol. 26,
Issue. 12,
p.
1647.
Hansen, Brian
Lund, Torben E.
Sangill, Ryan
and
Jespersen, Sune Nørhøj
2013.
Experimentally and computationally fast method for estimation of a mean kurtosis.
Magnetic Resonance in Medicine,
Vol. 69,
Issue. 6,
p.
1754.
Ford, J. S.
and
Andrews, D. L.
2014.
One- and two-photon absorption in solution: The effects of a passive auxiliary beam.
The Journal of Chemical Physics,
Vol. 141,
Issue. 3,
Williams, Mathew D.
Bradshaw, David S.
and
Andrews, David L.
2016.
Symmetry analysis of Raman scattering mediated by neighboring molecules.
The Journal of Chemical Physics,
Vol. 145,
Issue. 18,
Kjølby, B.F.
Khan, A.R.
Chuhutin, A.
Pedersen, L.
Jensen, J.B.
Jakobsen, S.
Zeidler, D.
Sangill, R.
Nyengaard, J.R.
Jespersen, S.N.
and
Hansen, B.
2016.
Fast diffusion kurtosis imaging of fibrotic mouse kidneys.
NMR in Biomedicine,
Vol. 29,
Issue. 12,
p.
1709.
Hansen, Brian
Lund, Torben E.
Sangill, Ryan
Stubbe, Ebbe
Finsterbusch, Jürgen
and
Jespersen, Sune Nørhøj
2016.
Experimental considerations for fast kurtosis imaging.
Magnetic Resonance in Medicine,
Vol. 76,
Issue. 5,
p.
1455.
Ee, June-Haak
Jung, Dong-Won
Kim, U-Rae
and
Lee, Jungil
2017.
Combinatorics in tensor-integral reduction.
European Journal of Physics,
Vol. 38,
Issue. 2,
p.
025801.
Hansen, Brian
and
Jespersen, Sune N.
2017.
Recent Developments in Fast Kurtosis Imaging.
Frontiers in Physics,
Vol. 5,
Issue. ,
Grbčić, Sara
Ibrahimbegović, Adnan
and
Jelenić, Gordan
2018.
Variational formulation of micropolar elasticity using 3D hexahedral finite-element interpolation with incompatible modes.
Computers & Structures,
Vol. 205,
Issue. ,
p.
1.
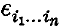 is 0 if any two of the i1 to in are equal, 1 if i1…in is an even permutation of 1, 2, 3, …,n, and – 1 if it is an odd permutation.
is 0 if any two of the i1 to in are equal, 1 if i1…in is an even permutation of 1, 2, 3, …,n, and – 1 if it is an odd permutation.