Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spencer, Craig V.
2009.
The Manin conjecture for x0y0+⋯+xsys=0.
Journal of Number Theory,
Vol. 129,
Issue. 6,
p.
1505.
Swinnerton-Dyer, Peter
2011.
Arithmetic Geometry.
Vol. 2009,
Issue. ,
p.
45.
Derenthal, U.
and
Frei, C.
2014.
On Manin's Conjecture for a Certain Singular Cubic Surface Over Imaginary Quadratic Fields.
International Mathematics Research Notices,
Derenthal, Ulrich
and
Frei, Christopher
2014.
Counting imaginary quadratic points via universal torsors.
Compositio Mathematica,
Vol. 150,
Issue. 10,
p.
1631.
Pieropan, Marta
2016.
Imaginary quadratic points on toric varieties via universal torsors.
Manuscripta Mathematica,
Vol. 150,
Issue. 3-4,
p.
415.
de la Bretèche, Régis
Destagnol, Kevin
Liu, Jianya
Wu, Jie
and
Zhao, Yongqiang
2019.
On a certain non-split cubic surface.
Science China Mathematics,
Vol. 62,
Issue. 12,
p.
2435.
Derenthal, Ulrich
and
Pieropan, Marta
2019.
Cox rings over nonclosed fields.
Journal of the London Mathematical Society,
Vol. 99,
Issue. 2,
p.
447.


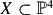 . In fact, if
. In fact, if 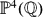 , then the height zeta function
, then the height zeta function 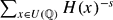 is analytically continued to the half-plane ℜ
is analytically continued to the half-plane ℜ