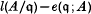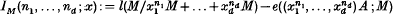Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cuong, Nguyen Tu
1992.
On the least degree of polynomials bounding above the differences between lengths and multiplicities of certain systems of parameters in local rings.
Nagoya Mathematical Journal,
Vol. 125,
Issue. ,
p.
105.
Cuong, Nguyen Tu
and
Khoi, Vu The
1996.
On the partial Euler-Poincare characteristics of certain systems of parameters in local rings.
Mathematische Zeitschrift,
Vol. 222,
Issue. 3,
p.
383.
Cuong, N. T.
and
Minh, N. D.
1996.
On the lengths of Koszul homology modules and generalized fractions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 120,
Issue. 1,
p.
31.
Cuong, Nguyen
1998.
Remarks on the non-Cohen-Macaulay locus of Noetherian schemes.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 4,
p.
1017.
Cuong, Nguyen Tu
Morales, Marcel
and
Nhan, Le Thanh
2003.
On the length of generalized fractions.
Journal of Algebra,
Vol. 265,
Issue. 1,
p.
100.
Cuong, Nguyen Tu
and
Nhan, Le Thanh
2003.
Pseudo Cohen–Macaulay and pseudo generalized Cohen–Macaulay modules.
Journal of Algebra,
Vol. 267,
Issue. 1,
p.
156.
Nhan, Le Thanh
2006.
A remark on the monomial conjecture and Cohen-Macaulay canonical modules.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 10,
p.
2785.
Kawasaki, Takesi
2007.
Finiteness of cousin cohomologies.
Transactions of the American Mathematical Society,
Vol. 360,
Issue. 5,
p.
2709.
CUONG, NGUYEN TU
and
CUONG, DOAN TRUNG
2007.
dd-SEQUENCES AND PARTIAL EULER–POINCARÉ CHARACTERISTICS OF KOSZUL COMPLEX.
Journal of Algebra and Its Applications,
Vol. 06,
Issue. 02,
p.
207.
Cuong, Nguyen Tu
Nhan, Le Thanh
and
Nga, Nguyen Thi Kieu
2010.
On pseudo supports and non-Cohen–Macaulay locus of finitely generated modules.
Journal of Algebra,
Vol. 323,
Issue. 10,
p.
3029.
Quy, Pham Hung
2013.
On the uniform bound of the index of reducibility of parameter ideals of a module whose polynomial type is at most one.
Archiv der Mathematik,
Vol. 101,
Issue. 5,
p.
469.
Dung, Nguyen Thi
2014.
SOME CHARACTERIZATIONS OF COHEN-MACAULAY MODULES IN DIMENSION > s.
Bulletin of the Korean Mathematical Society,
Vol. 51,
Issue. 2,
p.
519.
Cuong, Nguyen Tu
Long, Nguyen Tuan
and
Truong, Hoang Le
2015.
Uniform Bounds in Sequentially Generalized Cohen–Macaulay Modules.
Vietnam Journal of Mathematics,
Vol. 43,
Issue. 2,
p.
343.
Cường, Đoàn Trung
and
Nam, Phạm Hồng
2015.
Hilbert coefficients and partial Euler–Poincaré characteristics of Koszul complexes of d-sequences.
Journal of Algebra,
Vol. 441,
Issue. ,
p.
125.
Cuong, Nguyen Tu
and
Cuong, Doan Trung
2017.
Local Cohomology Annihilators and Macaulayfication.
Acta Mathematica Vietnamica,
Vol. 42,
Issue. 1,
p.
37.
Morales, Marcel
and
Quy, Pham Hung
2017.
A Study of the Length Function of Generalized Fractions of Modules.
Proceedings of the Edinburgh Mathematical Society,
Vol. 60,
Issue. 3,
p.
721.
Nam, Pham Hong
2025.
Unmixed torsions and Hilbert coefficients of d-sequences.
Journal of Algebra,
Vol. 664,
Issue. ,
p.
738.
Tu Cuong, Nguyen
and
Quy, Pham Hung
2025.
On the structure of finitely generated modules and the unmixed degrees.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 7,
p.
108000.