No CrossRef data available.
Article contents
Quadratic Lyapunov functions for linear systems
Published online by Cambridge University Press: 24 October 2008
Abstract
The paper deals with the existence of a quadratic Lyapunov function V = x′P(t)x for an exponentially stable linear system with varying coefficients described by the vector differential equation 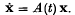 The derivative dV/dt is allowed to be strictly semi-(F) and the locus dV/dt = 0 does not contain any arc of the system trajectory. It is then shown that the coefficient matrix A(t) of the exponentially stable system is not identically equal to a unit matrix multiplied by a scalar. The result subsumes that of Lehnigk(1).
The derivative dV/dt is allowed to be strictly semi-(F) and the locus dV/dt = 0 does not contain any arc of the system trajectory. It is then shown that the coefficient matrix A(t) of the exponentially stable system is not identically equal to a unit matrix multiplied by a scalar. The result subsumes that of Lehnigk(1).
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 115 - 117
- Copyright
- Copyright © Cambridge Philosophical Society 1969
References
REFERENCES
(1)Lehnigk, S. H.Quadratic forms as Liapunov functions for linear differential equations with real constant coefficients. Proc. Cambridge Philos. Soc. 61 (1965), 883–888.CrossRefGoogle Scholar
(2)Malkin, I. G.On the construction of Lyapunov functions for systems of linear equations. Prikl. Mat. Meh. 16 (1952), 239–242.Google Scholar
(3)Coddington, B. A. and Levinson, N.Theory of ordinary differential equations (McGraw Hill; New York, 1955).Google Scholar
(4)Hahn, W.Theory and applications of Lyapunov's direct method (Prentice-Hall, Englewood Cliffs; N.J. 1963).Google Scholar

