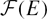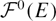Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Enescu, Florian
and
Yao, Yongwei
2016.
The Frobenius complexity of a local ring of prime characteristic.
Journal of Algebra,
Vol. 459,
Issue. ,
p.
133.
Graf, Patrick
and
Schwede, Karl
2017.
Discreteness of 𝐹-jumping numbers at isolated non-ℚ-Gorenstein points.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 2,
p.
473.
Patakfalvi, Zsolt
Schwede, Karl
and
Tucker, Kevin
2017.
Surveys on Recent Developments in Algebraic Geometry.
Vol. 95,
Issue. ,
p.
33.
De Stefani, Alessandro
Núñez-Betancourt, Luis
and
Pérez, Felipe
2018.
On the existence of 𝐹-thresholds and related limits.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 9,
p.
6629.
Chiecchio, Alberto
Enescu, Florian
Miller, Lance Edward
and
Schwede, Karl
2018.
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 17,
Issue. 1,
p.
171.
Enescu, Florian
and
Yao, Yongwei
2018.
On the Frobenius complexity of determinantal rings.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 2,
p.
414.
Page, Janet
2019.
The Frobenius complexity of Hibi rings.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 2,
p.
580.
Montaner, Josep Àlvarez
Boix, Alberto F.
and
Zarzuela, Santiago
2019.
A Koszul complex over skew polynomial rings.
Communications in Algebra,
Vol. 47,
Issue. 7,
p.
2904.
Boix, Alberto F.
and
Zarzuela, Santiago
2019.
Frobenius and Cartier Algebras of Stanley–Reisner Rings (II).
Acta Mathematica Vietnamica,
Vol. 44,
Issue. 3,
p.
571.
Alhazmy, Khaled
and
Katzman, Mordechai
2019.
FFRT properties of hypersurfaces and their F-signatures.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 11,
p.
1950215.
Àlvarez Montaner, Josep
2019.
Generating functions associated to Frobenius algebras.
Linear Algebra and its Applications,
Vol. 582,
Issue. ,
p.
310.
Enescu, Florian
and
Pérez, Felipe
2019.
The Frobenius exponent of Cartier subalgebras.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 9,
p.
3879.
MIYAZAKI, Mitsuhiro
2020.
Fiber cones, analytic spreads of the canonical and anticanonical ideals and limit Frobenius complexity of Hibi rings.
Journal of the Mathematical Society of Japan,
Vol. 72,
Issue. 3,
Badilla-Céspedes, Wágner
2021.
F-invariants of Stanley-Reisner rings.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 9,
p.
106671.
Walther, Uli
and
Zhang, Wenliang
2021.
Commutative Algebra.
p.
773.
Dao, Hailong
and
Montaño, Jonathan
2021.
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 6,
p.
1969.
Boix, Alberto F.
Gómez–Ramírez, Danny A. J.
and
Zarzuela, Santiago
2024.
On the Infinitely Generated Locus of Frobenius Algebras of Rings of Prime Characteristic.
Acta Mathematica Vietnamica,
Vol. 49,
Issue. 1,
p.
3.
Enescu, Florian
and
Yao, Yongwei
2024.
Graded rings of rational twist in prime characteristic.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 10,
p.
107691.
ENESCU, FLORIAN
2024.
A SHORT SURVEY ON FROBENIUS COMPLEXITY AND
GRADINGS WITH RATIONAL TWIST FOR RINGS OF PRIME
CHARACTERISTIC.
Revue Roumaine Mathematiques Pures Appliquees,
Vol. LXIX,
Issue. 3-4,
p.
505.