No CrossRef data available.
Article contents
Additive correlation and the inverse problem for the large sieve
Published online by Cambridge University Press: 09 July 2018
Abstract
Let A ⊆ [1, N] be a set of integers with |A| ≫ 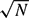 $\sqrt N$. We show that if A avoids about p/2 residue classes modulo p for each prime p, then A must correlate additively with the squares S = {n2 : 1 ≤ n ≤
$\sqrt N$. We show that if A avoids about p/2 residue classes modulo p for each prime p, then A must correlate additively with the squares S = {n2 : 1 ≤ n ≤ 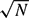 $\sqrt N$}, in the sense that we have the additive energy estimateThis is, in a sense, optimal.
$\sqrt N$}, in the sense that we have the additive energy estimateThis is, in a sense, optimal.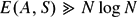 $$E(A,S)\gg N\log N.$$
$$E(A,S)\gg N\log N.$$
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 2 , March 2020 , pp. 211 - 217
- Copyright
- Copyright © Cambridge Philosophical Society 2018
References
REFERENCES
[BC] Bose, R. C. and Chowla, S. Theorems in the additive theory of numbers. Comment. Math. Helv. 37 (1962-63), 141–147.Google Scholar
[CL] Croot, E. S. III, and Lev, V. F. Open problems in additive combinatorics. In Additive combinatorics, volume 43 of CRM Proc. Lecture Notes, pages 207–233 (Amer. Math. Soc., Providence, RI, 2007).Google Scholar
[FI] Friedlander, J. and Iwaniec, H. Opera de cribro. American Mathematical Society Colloquium Publications, 57 (American Mathematical Society, Providence, RI, 2010).Google Scholar
[GH] Green, B. and Harper, A. J Inverse questions for the large sieve. Geom. Funct. Anal. 24 (4) (2014), 1167–1203.Google Scholar
[HV] Helfgott, H. A. and Venkatesh, A. How small must ill-distributed sets be? Analytic Number Theory, Essays in honour of Klaus Roth (Cambridge University Press 2009), 224–234.Google Scholar
[K] Kolountzakis, M. N. On the uniform distribution in residue classes of dense sets of integers with distinct sums. J. Number Theory 76 (1999), 147–153.Google Scholar
[La] Landau, E. Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate. Arch. Math. Phys. 13 (1908), 305–312.Google Scholar
[Li] Lindström, B. Well distribution of Sidon sets in residue classes. J. Number Theory 69 (1998), 197–200.Google Scholar
[M] Montgomery, H. L. A note on the large sieve. J. London Math. Soc. 43 (1968), 93–98.Google Scholar
[R] Ramanujan, S. Some formulae in the analytic theory of numbers. Messenger Math. 45 (1916), 81–84.Google Scholar
[W1] Walsh, M. N. The inverse sieve problem in high dimensions. Duke Math. J. 161 (2012), no. 10, 2001–2022.Google Scholar
[W2] Walsh, M. N. The algebraicity of ill-distributed sets. Geom. Funct. Anal. 24 (2014), no. 3, 959–967.Google Scholar

