Article contents
Additive structures in sumsets
Published online by Cambridge University Press: 01 March 2008
Abstract
Suppose that A and A′ are subsets of ℤ/Nℤ. We write A+A′ for the set {a+a′:a ∈ A and a′ ∈ A′} and call it the sumset of A and A′. In this paper we address the following question. Suppose that A1,. . .,Am are subsets of ℤ/Nℤ. Does A1+· · ·+Am contain a long arithmetic progression?
The situation for m=2 is rather different from that for m ≥ 3. In the former case we provide a new proof of a result due to Green. He proved that A1+A2 contains an arithmetic progression of length roughly 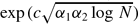 where α1 and α2 are the respective densities of A1 and A2. In the latter case we improve the existing estimates. For example we show that if A ⊂ ℤ/Nℤ has density
where α1 and α2 are the respective densities of A1 and A2. In the latter case we improve the existing estimates. For example we show that if A ⊂ ℤ/Nℤ has density 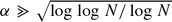 then A+A+A contains an arithmetic progression of length Ncα. This compares with the previous best of Ncα2+ϵ.
then A+A+A contains an arithmetic progression of length Ncα. This compares with the previous best of Ncα2+ϵ.
Two main ingredients have gone into the paper. The first is the observation that one can apply the iterative method to these problems using some machinery of Bourgain. The second is that we can localize a result due to Chang regarding the large spectrum of L2-functions. This localization seems to be of interest in its own right and has already found one application elsewhere.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 289 - 316
- Copyright
- Copyright © Cambridge Philosophical Society 2008
References
REFERENCES
- 20
- Cited by

