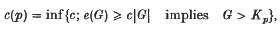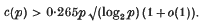Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Woodall, D. R.
1987.
Subcontraction‐equivalence and Hadwiger's conjecture.
Journal of Graph Theory,
Vol. 11,
Issue. 2,
p.
197.
Thomason, Andrew
1987.
Annals of Discrete Mathematics (33), Proceedings of the International Conference on Finite Geometries and Combinatorial Structures.
Vol. 144,
Issue. ,
p.
307.
Jørgensen, L.K.
1988.
Graph Theory in Memory of G.A. Dirac.
Vol. 41,
Issue. ,
p.
307.
Haviland, Julie
and
Thomason, Andrew
1989.
Pseudo-random hypergraphs.
Discrete Mathematics,
Vol. 75,
Issue. 1-3,
p.
255.
Duchet, Pierre
and
Kaneti, Viktor
1994.
Sur la contractibilité d'un graphe orienté en K∗4.
Discrete Mathematics,
Vol. 130,
Issue. 1-3,
p.
57.
1994.
Graph Coloring Problems.
p.
109.
Gustedt, Jens
and
Steger, Angelika
1994.
Orders, Algorithms, and Applications.
Vol. 831,
Issue. ,
p.
100.
Seymour, Paul
1995.
Proceedings of the International Congress of Mathematicians.
p.
183.
Bollob�s, B�la
and
Thomason, Andrew
1996.
Highly linked graphs.
Combinatorica,
Vol. 16,
Issue. 3,
p.
313.
Diestel, Reinhard
1996.
Graphentheorie.
p.
153.
Reed, Bruce
and
Seymour, Paul
1998.
Fractional Colouring and Hadwiger's Conjecture.
Journal of Combinatorial Theory, Series B,
Vol. 74,
Issue. 2,
p.
147.
Gustedt, Jens
1998.
STACS 98.
Vol. 1373,
Issue. ,
p.
421.
Ding, Guoli
Oporowski, Bogdan
Sanders, Daniel P.
and
Vertigan, Dirk
2000.
Surfaces, Tree-Width, Clique-Minors, and Partitions.
Journal of Combinatorial Theory, Series B,
Vol. 79,
Issue. 2,
p.
221.
Reed, Bruce
and
Thomas, Robin
2000.
Clique Minors in Graphs and Their Complements.
Journal of Combinatorial Theory, Series B,
Vol. 78,
Issue. 1,
p.
81.
Thomason, Andrew
2000.
Complete minors in pseudorandom graphs.
Random Structures and Algorithms,
Vol. 17,
Issue. 1,
p.
26.
Grigni, Michelangelo
2000.
Automata, Languages and Programming.
Vol. 1853,
Issue. ,
p.
869.
Thomason, Andrew
2001.
The Extremal Function for Complete Minors.
Journal of Combinatorial Theory, Series B,
Vol. 81,
Issue. 2,
p.
318.
Galluccio, Anna
Goddyn, Luis A.
and
Hell, Pavol
2001.
High-Girth Graphs Avoiding a Minor are Nearly Bipartite.
Journal of Combinatorial Theory, Series B,
Vol. 83,
Issue. 1,
p.
1.
Nešetřil, Jaroslav
and
Ossona de Mendez, Patrice
2003.
Discrete and Computational Geometry.
Vol. 25,
Issue. ,
p.
651.
Myers, Joseph Samuel
2003.
The extremal function for unbalanced bipartite minors.
Discrete Mathematics,
Vol. 271,
Issue. 1-3,
p.
209.