An integral which occurs in statistics
Published online by Cambridge University Press: 24 October 2008
Extract
1. In this note we give a direct evaluation of the integral
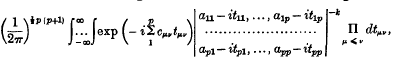
whose value has been inferred from the theory of statistics. Here A = Ap = (αμν) and C = Cp = (Cμν) are real symmetrical matrices, of which A is positive definite; there are ½ p (p + 1) independent variables of integration tμν (1 ≤ μ ≤ ν ≤ p), and tμν is written also as tνμ for symmetry of notation; in the summation ∑ the variables μ, ν run independently from 1 to p; k is a real number. A word of explanation is necessary with regard to the determination of the power |A − iT|−k. Since A is positive definite and T real and symmetric, the roots of the equation
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 2 , May 1933 , pp. 271 - 276
- Copyright
- Copyright © Cambridge Philosophical Society 1933
References
* Wishart, J., Biometrika, 20 A (1928), 32–52CrossRefGoogle Scholar; Wishart, J. and Bartlett, M. S., Proc. Camb. Philos. Soc. 29 (1933), 260–270CrossRefGoogle Scholar (the paper preceding this).
† We denote a square matrix (αμν) of p rows and columns by A p or A, and its determinant by |A| or |A p|; with a similar notation in other letters. A real symmetric matrix A is ‘positive definite’ if the associated quadratic form ![]() is positive definite; by this we mean that A (x, x) > 0 for all real values of x 1, …, x p not all 0 (i.e. we use ‘positive definite’ in the sense of ‘positive and non-singular’ or ‘positive and of rank p’).
is positive definite; by this we mean that A (x, x) > 0 for all real values of x 1, …, x p not all 0 (i.e. we use ‘positive definite’ in the sense of ‘positive and non-singular’ or ‘positive and of rank p’).
To avoid confusion with the notation |A| we denote the modulus of a complex number z by |z|, and the modulus of |A| by |A|.
* Cf. Wishart and Bartlett, loc. cit., 261. To reduce our integral to their form (c) we take the integrals along the imaginary axes (as we may by Cauchy's theorem) and write υμ = iu μ, noting that ![]()
- 41
- Cited by

