Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T09:39:34.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic density in quasi-logarithmic additive number systems

Published online by Cambridge University Press:  01 March 2008

BRUNO NIETLISPACH
BRUNO NIETLISPACH*
Affiliation:
Institute of Mathematics, University of Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland. e-mail: bruno.nietlispach@math.uzh.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that in quasi-logarithmic additive number systems 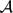all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function p(n) of the set of irreducible elements of allow situations which are not covered by the density theorems of Compton [6] and Woods [15]. We also give conditions on p(n) which are sufficient to show the assumptions of Compton's result are satisfied, but which are not necessarily implied by those of Bell and Burris [2], Granovsky and Stark [8] or Stark [14].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 267 - 287
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arratia, R., Barbour, A. D. and Tavaré, S.. Logarithmic combinatorial structures: a probabilistic approach. EMS Monographs in Mathematics (European Mathematical Society, Zürich, 2003).CrossRefGoogle Scholar
[2]Bell, J. P. and Burris, S. N.. Asymptotics for logical limit laws: when the growth of the components is in an RT class. Trans. Amer. Math. Soc. 355 (2003), 3777–3794 (electronic).CrossRefGoogle Scholar
[3]Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular variation. Encyclopedia Maths Appl. 27 (1989).Google Scholar
[4]Burris, S. N.Number theoretic density and logical limit laws. Math. Surveys Monogr. 86 (2001).CrossRefGoogle Scholar
[5]Chang, C. C. and Keisler, H. J.. Model theory. Stud. Logic Found. Math. 73 (1973).Google Scholar
[6]Compton, K. J.A logical approach to asymptotic combinatorics. II. Monadic second-order properties.. J. Combin. Theory Ser. A 50 (1989), 110–131.CrossRefGoogle Scholar
[7]Ebbinghaus, H.-D., Flum, J. and Thomas, W.. Mathematical logic. Undergraduate Texts in Mathematics (Springer, 1984).Google Scholar
[8]Granovsky, B. L. and Stark, D.Asymptotic enumeration and logical limit laws for expansive multisets and selections. J. London Math. Soc. (2) 73 (2006), 252–272.CrossRefGoogle Scholar
[9]Indlekofer, K.-H.Manstavičius, E. and Warlimont, R.. On a certain class of infinite products with an application to arithmetical semigroups. Arch. Math. (Basel) 56 (1991), 446–453.CrossRefGoogle Scholar
[10]Knopfmacher, A., Knopfmacher, J. and Warlimont, R.. “Factorisatio numerorum” in arithmetical semigroups. Acta Arith. 61 (1992), 327–336.CrossRefGoogle Scholar
[11]Knopfmacher, J. and Zhang, W.-B.Number theory arising from finite fields. Analytic and probabilistic theory. Monographs and Textbooks in Pure and Applied Mathematics 241 (Marcel Dekker, 2001).CrossRefGoogle Scholar
[12]Meir, A. and Moon, J. W.. On random mapping patterns. Combinatorica 4 (1984), 61–70.CrossRefGoogle Scholar
[13]Nietlispach, B. Quasi-logarithmic structures. PhD thesis. Zurich (2007).Google Scholar
[14]Stark, D.Logical limit laws for logarithmic structures. Math. Proc. Camb. Phil. Soc. 140 (2006), 537–544.CrossRefGoogle Scholar
[15]Woods, A. R.Counting finite models. J. Symbolic Logic 62 (1997), 925–949.CrossRefGoogle Scholar