Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-07T12:54:57.107Z Has data issue: false hasContentIssue false
  • English
  • Français

The classification of rank 3 reflective hyperbolic lattices over 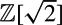$\mathbb{Z}[\sqrt{2}]$

Published online by Cambridge University Press:  09 December 2016

ALICE MARK
ALICE MARK*
Affiliation:
School of Mathamatical and Statistical Sciences, Arizona State University, P.O. Box 871804, Tempe, AZ 85287-1804, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

There are 432 strongly squarefree symmetric bilinear forms of signature (2, 1) defined over 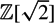$\mathbb{Z}[\sqrt{2}]$ whose integral isometry groups are generated up to finite index by finitely many reflections. We adapted Allcock's method (based on Nikulin's) of analysis for the 2-dimensional Weyl chamber to the real quadratic setting, and used it to produce a finite list of quadratic forms which contains all of the ones of interest to us as a sub-list. The standard method for determining whether a hyperbolic reflection group is generated up to finite index by reflections is an algorithm of Vinberg. However, for a large number of our quadratic forms the computation time required by Vinberg's algorithm was too long. We invented some alternatives, which we present here.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 2 , March 2018 , pp. 221 - 257
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Agol, I. Finiteness of arithmetic Kleinian reflection groups. In Proceedings of the International Congress of Mathematicians (Madrid, August 22-30, 2006) invited lectures. (2006), pp. 951–960.Google Scholar
[2] Agol, I., Belolipetsky, M., Storm, P. and Whyte, K. Finiteness of arithmetic hyperbolic reflection groups. arXiv preprint math.GT/0612132, (2006).Google Scholar
[3] Allcock, D. The reflective lorentzian lattices of rank 3. American Mathematical Soc. (2012).CrossRefGoogle Scholar
[4] Bartlett, P. Finding all the roots: Sturm's theorem. Mathcamp (2013).Google Scholar
[5] Belolipetsky, M. Arithmetic hyperbolic reflection groups. ArXiv e-prints (June 2015).Google Scholar
[6] Bugaenko, V. O. Groups of automorphisms of unimodular hyperbolic quadratic forms over the ring $\mathbb{Z} \left[{(\sqrt{5}+ 1})/{2}\right]$ . Moscow Univ. Math. Bull. 39 (1984), 6–14.Google Scholar
[7] Bugaenko, V. O. On reflective unimodular hyperbolic quadratic forms. Selecta Math. Soviet. 9 (3) (1990), 263–271.Google Scholar
[8] Bugaenko, V. O. Arithmetic crystallographic groups generated by reflections, and reflective hyperbolic lattices. Lie groups, their discrete subgroups and invariant theory. 8 (1992), 33–55.Google Scholar
[9] Koch, H. Number Theory: Algebraic Numbers and Functions. Graduate Studies in Mathematics. American Mathematical Society (2000).Google Scholar
[10] Long, D. D., Maclachlan, C. and Reid, A. W. Arithmetic fuchsian groups of genus zero. Pure Appl. Math. Quart. 2 (2) (2006), 569–99.Google Scholar
[11] Mark, A. The classification of rank 3 reflective hyperbolic lattices over $\mathbb{Z}[\sqrt{2}]$ . ArXiv e-prints (December 2015).Google Scholar
[12] Nikulin, V. V. On arithmetic groups generated by reflections in lobachevsky spaces. Math. USSR-Izvestiya 16 (3) (1981), 573.Google Scholar
[13] Nikulin, V. V. On the classification of arithmetic groups generated by reflections in lobachevsky spaces. Math. USSR-Izvestiya 18 (1) (1982), 99.Google Scholar
[14] Nikulin, V. V. On the classification of hyperbolic root systems of rank three. Proceedings of the Steklov Institute of Mathematics. Maik Nauka/Interperiodica Publ. (2000).Google Scholar
[15] Nikulin, V. V. Finiteness of the number of arithmetic groups generated by reflections in lobachevsky spaces. Izv. Math. 71 (1) (2007), 53.CrossRefGoogle Scholar
[16] O'Meara, O. T. Introduction to Quadratic Forms. Classics in Mathematics (Springer, Berlin Heidelberg, 1999).Google Scholar
[17] Takeuchi, K. et al. Arithmetic triangle groups. J. Math. Soc. Japan 29 (1) (1977), 91–106.Google Scholar
[18] The PARI Group (Bordeaux). PARI/GP version 2.5.4, 2014. Available from http://pari.math.u-bordeaux.fr/.Google Scholar
[19] Vinberg, È. B. On groups of unit elements of certain quadratic forms. Sb. Math. 16 (1) (1972), 17–35.Google Scholar
[20] Vinberg, È. B. Hyperbolic reflection groups. Russian Math. Surveys 40 (1) (1985), 31.CrossRefGoogle Scholar
[21] Vinberg, È. B. and Kaplanskaja, I. M. On the groups o 18,1(ℤ) and o 19,1(ℤ). (Russian) Dokl. Akad. 238 (1978), 1273–1275.Google Scholar